欠驱动刚性航天器可行轨迹生成算法研究

马广富，庄宇飞，李传江，黄海滨

(哈尔滨工业大学航天学院，哈尔滨150001)

0 Introduction

The problem of rigid spacecraft attitude control using less than three control inputs has received a lot of attention during the last decade［1－8］，especially for the axisymmetric cases．Until now，the stabilization problem for axisymmetric cases can be considered solved［3－6］，and yet，compared with the results on stabilizability，the trajectory tracking problem for an underactuated spacecraft turns out to be much more challenging．In Ref．［4］，it is assumed that the reference trajectory is given by a‘virtual’system in order to guarantee the desired attitude histories feasible，and then a tracking control law is proposed for the axisymmetric spacecraft．In this paper，we consider the feasible trajectory generation problem of an axisymmetric underactuated spacecraft and the obtained trajectories can be regarded as feasible reference trajectories for further tracking problems．Instead of using the nonstandard(w，z)attitude parameterization［3－6］，we use the most popular Euler angles parameterization which is physically intuitive，and the corresponding flat outputs can also be easily found in this case．

Firstly，we derive the conditions which must be satisfied by the attitude history as a feasible trajectory;then from kinematics equations of the underactuated spacecraft，a set of flat outputs are deduced，and based on the differential flatness property of system，a method to generate feasible trajectories is proposed．By using a novel form of flat output basis function，the corresponding angular velocity and input commands can be kept in a small and reasonable scope all the time，even for a large angle maneuver of the spacecraft，and singular avoidance problem also can be simplified by using this set of flat outputs．

1 Kinematics equations

By using the body 3－2－1 sequenced rotation，in terms of Euler angles parameterization，the kinematics equations of an underactuated spacecraft can be described as

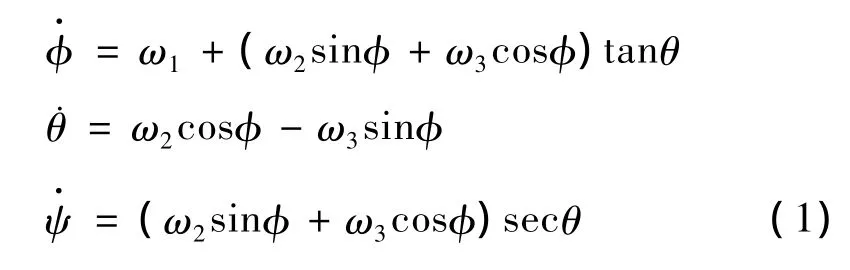
Without loss of generality，assuming the 3-axis of the spacecraft is symmetric and underactuated axis．Thus，it is obvious that the angular velocity component ω3along the 3-axis with no control torques remains constant for all t≥0．It is known that in this case，the complete system fails to be controllable or even accessible，unless the angular velocity along the uncontrolled axis is zero(in case of gas jets)．Thus letω3(0)=0，i．e．，ω3≡0，then Eq．(1)becomes

And state variable x=［ω1，ω2，ω3，φ，θ，ψ］Tis defined on an open set as

Additionally，the corresponding dynamic equations are

where ui(i=1，2)is the input torque along the ith body axis．Assuming angular velocityω1andω2can be manipulated，and then the following design is performed only on kinematics level．Since from the dynamic equations of the axisymmetric system，it is easily to‘backstep’the kinematics control laws to the dynamic ones［4］．

2 Feasible trajectory generation

2．1 Constraint on attitude history

In Eq．(2)，ωi(i=1，2)is regarded as control input，sinceω3≡0，the attitude variablesφ，θ，ψcannot be functionally independent．That is，in the absence of control torque along the symmetric axis，we cannot except to track any trajectories as we wish［5］．From Eq．(2)，we obtain the constraint for feasible attitude trajectory

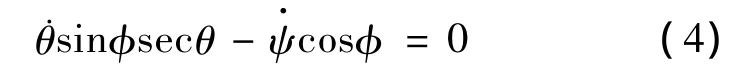
From this constraint，it is obvious that，the attitude history must satisfy the sufficient and necessary condition of Eq．(4)in order to be a feasible trajectory．

In the following section，we would propose a method to generate feasible trajectory for system(2)，which can be used as reference trajectory for further attitude tracking problem．In particular，for given initial point(φ0，θ0，ψ0)T，final point(φf，θf，ψf)Tand time tf，we should find time functionsφ(t)，θ(t)，ψ(t)defined over the interval 0≤t≤tf，and satisfying Eq．(4)for all 0≤t≤tf［5］．We call such trajectories feasible，since they ensure the existence of angular velocityωi(i=1，2)，and they also make the condition(4)satisfied．

2．2 Differential flatness

To solve the feasible trajectory generation problem，we introduce the notation of differential flatness［5，8－10］．A control system

is differentially flat，if we can find output y∈Rmof the form

and locally surjective A and B，such that

whereρand r are positive integers，y is called a set of flat outputs．In other words，a system with m inputs is flat，if there exist m output functions y1，y2，…，ymthat parameterize the state x and input u．This property is quite important，because once a set of suitable flat output trajectories y(t)is found，the corresponding state and control input trajectories both can be determined by Eq．(7)．Therefore，differentially flat systems are ideally suitable for trajectory generation tasks;however，this approach is not without its shortcomings．Although flatness is a geometric property of common systems，there is no systematic way to find flat outputs for most systems．Moreover，in the following design，another problem should be taken into account is the singular cases which arise during the flat transformation from flat output space to state and input spaces as described in Eq．(7)．

2．3 Flat outputs for kinematics equations

From Eq．(2)and the definition of flatness，if axisymmetric underactuated system is differentially flat，the corresponding flat outputs for the axisymmetric spacecraft must necessarily explicitly depend on variableψ［8］．

Proposition 1．The kinematic model of an axisymmetric underactuated spacecraft as Eq．(2)is differentially flat，and one set of the feasible flat outputs is y=(θ，ψ)．

Proof．From Eq．(2)，we can obtain the following relationships

Obviously，variablesω1，ω2，φall depend onθ，ψ．Therefore，y1=θ，y2=ψcan be denoted as flat outputs，and before parameterizingφwith flat outputs and their derivatives，we define a function first．

Definition 1．Let arctan*(·，·)be an arctangent function with two variables(r1，r2)，which uses the signs of both r1and r2to determine the quadrant，in which the resulting angle lies．The explicit expression of function arctan*(r1，r2)［8］is arctan*(r1，r2)

Then from the above Eq．(8)and Eq．(9)，it can be obtained that

Thus all attitude variablesφ，θ，ψcan be written as algebraic functions of flat outputs y1，y2and their derivatives．

Moreover，from Eq．(8)ω1，ω2can also be written as functions of y1，y2and their derivatives as follows

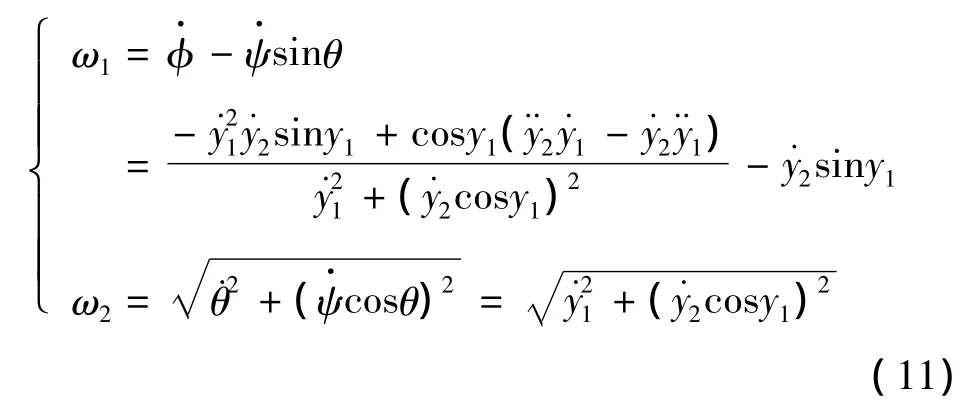
From previous derivation，we can deduce that the underactuated axisymmetric spacecraft is differentially flat with flat output y=(θ，ψ)．

2．4 Feasible trajectory generation algorithm

Now we consider the problem of generating feasible trajectories for flat system(2)from an initial point(φ(0)，θ(0)，ψ(0))T=(φ0，θ0，ψ0)Tto the final point(φ(tf)，θ(tf)，ψ(tf))T=(φf，θf，ψf)Tat time t=tf．We first construct paths on y1－y2plane，and then map them back to the attitude space using Eq．(10)and angular velocity space using Eq．(11)．By choosing different flat output basis functions，paths on y1－y2plane can be chosen arbitrarily，as long as they satisfy the above boundary conditions．In this paper，to simplify the design of flat outputs，we assume the component of the flat outputs y1(t)has a simple polynomial form as follows

and then，solve the coefficients ai(i=0，1)on the constraints of two end points y10=θ0，y1f=θf，which give rise to a linear system of equations．Since t0≠tfand t0=0，a unique solution of above linear equations for ai(i=0，1)can be obtained．And the non-zero coefficients for trajectory y1(t)=θ(t)are a0=θ0，a1=(θf－ θ0)/tf．

Generally，for simplification，the basis functions of flat outputs are always chosen in the form of polynomials as y1(t)［8］．However，the previous two flat outputs y1，y2are the corresponding Euler angles of an underactuated spacecraft，with a range y1=θ∈(－π/2，π/2)，y2=ψ ∈［－ π，π］．From Eq．(9)and Eq．(12)，it is found thatφ，θcan be well kept in the corresponding ranges．And yet，the range ofψ=y2is not considered in the whole operation．Especially for a large angle maneuver case，the value ofψmay exceed the range［－π，π］，and then the angular velocity commands should also be large enough to steer the spacecraft the large angle．In order to solve this problem，we propose a novel form of basis function for flat output y2to guaranteeψ=y2always in its range．

Assuming y2(t)is parameterized in terms of function y1(t)，thus we let y2(t)written in the following

where we obtain the coefficients bi(i=0～3)．And once the time functions y1(t)and y2(t)are known from the equations above，we can have both the attitude trajectories and input trajectories in terms of time t from Eq．(10)and Eq．(11)．

Another problem occurred in the transformation from flat outputs space to attitude and input spaces is the singularity avoidance．Eq．(10)has a singularity at=0 and Eq．(11)has another singularity at=0．It is easily to observe that oncethe singularity in Eq．(11)would not arise，i．e．，we need only solve the singularity avoidance problem of=0 in Eq．(10)，and the singular case in Eq．(11)can then be solved simultaneously．Further，from Eq．(12)，we can obtainwhich makes the condition˙y1≠0 satisfied and also makesin Eq．(11)，so there is no singularities reached in the whole flat transformation．

3 Simulation results

In this section，the algorithm for feasible trajectoform as

where bi(i=0～3)are four unknown coefficients．So that，y2(t)is a continuous function in the range［－π，π］and has a definition domain(－∞，+∞)．Additionally，there are no singular points arising in y2and its all-order derivatives．

The previous parameterization implies ry generation is demonstrated．We assume that the spacecraft is steered from an initial orientation(φ0，θ0，ψ0)T=(π/4，－ π/3，－ π/2)Tto final orientation(φf，θf，ψf)T=(－ π/4，π/3，π/2)T，and tf=20s．Fig．1 shows the flat output trajectory of y2in terms of y1．And the corresponding feasible trajectories mapped in the attitude and angular velocity spaces are shown in Fig．2 and Fig．3．It is obvious that by using the novel form of basis function for flat output y2，we can guarantee the angleψ=y2always stay in the range［－π，π］，and the angular velocity can also be maintained as a relative small and suitable value．Comparing with another feasible trajectory generation method based on(w，z)attitude parameterization in Ref．［5］，the flat outputs proposed in this paper are more physically intuitive，and can be deduced straight forward，and the form of y1(t)need not change as in Ref．［5］，even for some special end points conditions．Additionally，since φ，θ，ψandω1，ω2can be parameterized with flat outputs y1，y2and their derivatives in more simple form，the consumption of calculation time is smaller，which makes the real-time on-line motion planning and trajectory tracking possible．

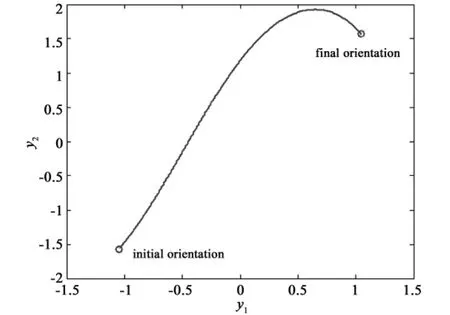
Fig．1 Trajectory in flat output space

4 Conclusions

Fig．2 Feasible trajectories in attitude space

Fig．3 Feasible angular velocity commands

In this paper，the problem of feasible trajectory generation of an axisymmetric underactuated spacecraft with two control torques acting on the plane orthogonal to the symmetric axis is solved．We firstly derive the sufficient and necessary conditions that must be satisfied for a feasible trajectory．And then based on differential flatness property of the system，an algorithm for generating feasible trajectory is proposed，which satisfies the constraints．We use a novel flat output basis function，which guarantees the angular velocity and control torques commands always in a reasonable range，even in case of large angle maneuver．Finally，a singularity avoidance methodology is proposed in order to make attitude and input trajectories non-singular everywhere in the flat output space．The feasible trajectories generated by the previous approach can be used in further trajectory tracking problem．

［1］Coron J M，Kerai E L．Explicit feedback stabilizing the attitude of a rigid spacecraft with two control torques［J］．Automatica，1996，36(5):669－677．

［2］Morin P，Samson C．Time-varying stabilization of a rigid spacecraft with two control torques［J］．IEEE Transactions on Automatic Control，1997，42(4):528－534．

［3］Tsiotras P，Luo J．Reduced-effort control laws for underactuated rigid spacecraft［J］．Journal of Guidance，Control，and Dynamics，1997，20(6):1089－1095．

［4］Tsiotras P，Luo J．Stabilization and tracking of underactuated axisymmetric spacecraft with bounded control［C］．The 4th IFAC Nonlinear Control Systems Design Symposium，Twente，Netherlands，July，1998．

［5］Tsiotras P．Feasible trajectory generation for underactuated spacecraft using differential flatness［C］．AASAstrodynamics Specialists Conference，Alaska，USA，August，1999．

［6］Tsiotras P，Doumtchenko V．Control of spacecraft subject to actuator failures:state-of-the-art and open problems［J］．Journal of the Astronautical Sciences，2000，48(2):337－358．

［7］Ge X S，Sun PW．Nonholonomic motion planning for the attitude of underactuated spacecraft using particle swarm optimization［J］．Journal of Astronautics，2006，27(6):1233－1237．

［8］Aguilar CO．Attitude control of a differentially flat underactuated rigid spacecraft［D］．Canada:University of Alberta，2005．

［9］Fliess M，Levine J，Martin P，et al．Flatness and defect of nonlinear systems:introductory theory and examples［J］．International Journal of Control，1995，61(9):1327－1361．

［10］Fliess M，Levine J，Martin P，et al．A lie-backlund approach to equivalence and flatness of nonlinear systems［J］．IEEE Transactions on Automatica Control，1999，44(5):922－937．