一种基于精英种子策略的多目标遗传算法

李文彬 , 杜若川, 李雄略, 尹 呈, 郭观七

(湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006)

引言

多目标优化(MO: Multi-objective Optimization)是工程实践中的常见问题, 其主要特点是各目标之间存在冲突, 目标之间无法同时取得最优值, 只能找到一组Pareto非劣解. 但在工程实践中, 人们往往知道在目标空间中满足一定条件的一个或几个最优解, 因此这就需要在这一特定的区域能够得到比较稠密的Pareto解, 这就对优化算法提出了新的问题, 要求在寻优过程中必须把已知的最优解加到初始种群中去,让这些最优解信息来引导寻优方向, 从而在感兴趣的区间内产生能够满足人们需要的Pareto解. 针对这个问题, 本文提出了基于精英种子策略的多目标遗传算法, 把已知的最优解信息加到优化过程中, 并利用最近邻方法来识别个体的优略, 引导优化方向, 通过仿真把该算法和NSGA-Ⅱ[1]进行比较, 结果证明了该算法的可行性和有效性.

1 多目标优化问题

一般一个MOP包括n个决策变量, r个目标函数, k个约束条件. 假设优化目标之间是相互冲突的, 则一个最小MOP问题可以表示为:

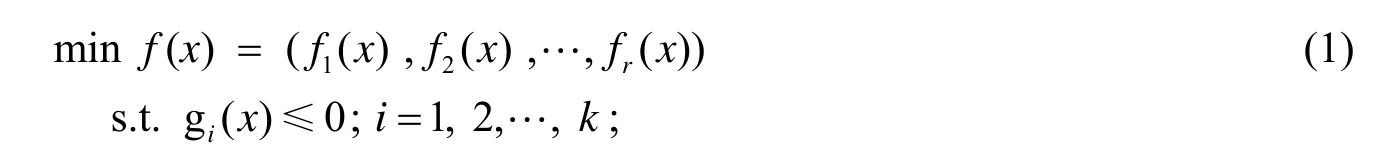
定义 1 设 P为一个集合, 其大小为n, P中每一个个体均有r个属性,是每个属性的评价函数(k= 1,2,… ,r), P中个体之间的关系定义为:

定义2 非支配集: 对于给定个体x∈P, 若∄y∈P, 使, 则x称之为集合P的非支配个体. 由所有P的非支配个体组成的集合, 称之为P的非支配集.

定义3 设Nds是P的非支配集, 则Nds⊆P, ∀x∈P若x是P的非支配个体, 必有, 则称Nds是P的最大非支配集.

2 基于最近邻方法的精英选择

2.1 最近邻方法

显然, 两个模式越相似, 距离d ( · )就越小. 反之亦然.

2.2 精英选择

在工程实践的多目标优化问题中, 人们往往知道目标空间中的一个或几个最优解, 因此我们把这些已知的最优解作为进化寻优过程中的精英种子, 引导优化方向, 加快pareto最优解收敛的速度. 具体做法是: 首先把精英种子加入到初始产生的种群中去, 并对该种群利用擂台法则[3]产生占优类、次优类和劣类,那么已知的精英种子一定在占优类中; 然后对个体进行选择、进化, 产生新的个体, 再对新个体利用最近邻方法进行识别, 使靠近pareto面的精英个体不断加入到占优类中. 这样占优类中既包含了原有的精英个体, 也包含了从进化种群中迁移过来的属于精英种群的优秀个体, 加快了寻找最优Pareto 解的速度.

3 基于精英种子策略的多目标遗传算法

算法采用了精英种子个体保留策略来保证能够收敛到问题真正的 Pareto 解. 在种群的进化过程中引入已知的最优个体信息, 把这些已知的最优精英个体加入到占优类中, 并利用最近邻方法把靠近pareto面的个体保留下来, 从而能够在此区域内得到足够多的Pareto 解.

基于精英种子策略的多目标遗传算法的步骤为:

步骤1 设置参数, 初始化种群, 把已知最优个体加入到初始种群中(种群中个体数目popsize、运算代数Maxgen、变量个数fnvar=2、已知最优个体集合KnowClass; 创建初始种群pop, 合并KnowClass与pop, 并置代数gen=0);

步骤2 if mod(gen,5)==0 用擂台法则产生非支配类、支配类和不相关类; 否则转步骤3;

步骤3 根据rank和拥挤距离选择个体, 遗传进化;

步骤4 用最近邻方法识别个体所属占优类、次优类和劣类;

步骤5 gen=gen+1, 如果gen≤Maxgen, 转到步骤2, 否则终止.

本算法在遗传算法进化过程中用最近邻方法识别个体, 把与精英种子距离最小的个体都放到了占优类中, 然后对个体进行选择, 并且随着遗传寻优过程的进行, 占优类中的个体也在不断的进化. 这样, 既保证了遗传算法能够在整个目标空间内进行寻优、避免出现早熟现象, 又能够在特定的区域内产生比较稠密的Pareto解.

4 实验与仿真比较

为检验所提出的算法的有效性, 对ZDT1、ZDT2和ZDT3这三个有代表的多目标优化问题分别以遗传算法中效果比较好的 NSGA-Ⅱ算法和基于精英种子策略的多目标遗传算法进行计算和比较. 对NSGA-Ⅱ算法取种群规模为 100 个, 进化代数为 100 代. 对基于精英种子策略的多目标遗传算法种群规模为100 个, 其中精英种子(已知最优解个体)3个, 进化代数20代.

ZDT1函数的两种算法仿真结果如下:

(1)图1～4为基于精英种子策略的多目标遗传算法;

(2)图5、6为NSGA-Ⅱ算法.

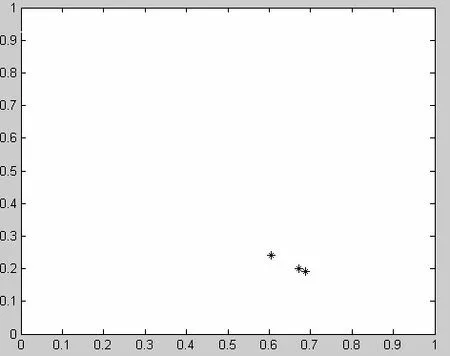
图1 初始精英种子(已知最优解个体)3个

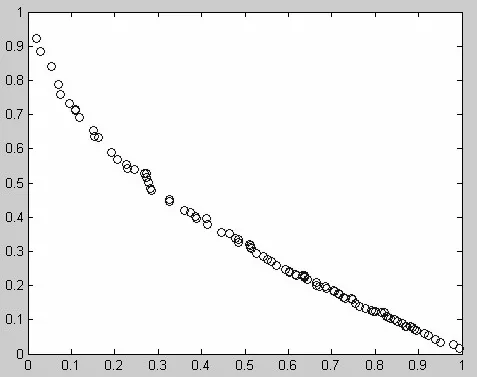
图2 第5代结果

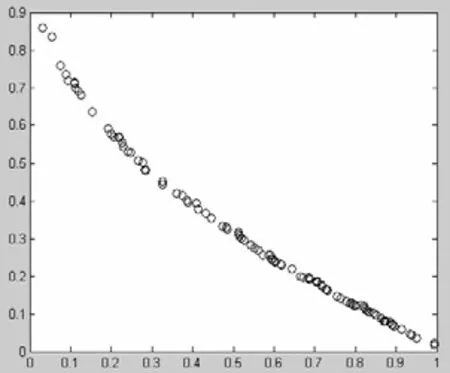
图3 第15代结果

图4 第20代结果

图5 第20代结果

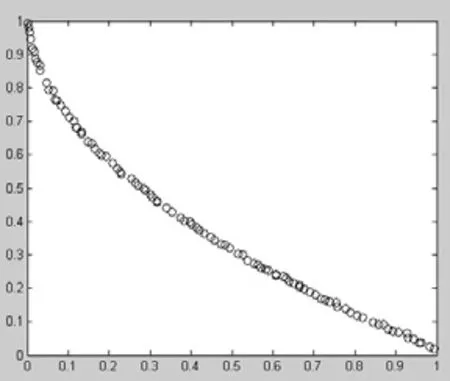
图6 第100代结果

从ZDT1函数两种方法的仿真过程可以得出, 在基于精英种子策略的多目标遗传算法中从第5代就可以很快的得到想要的解, 而在接下来的进化过程中, 仅仅是在某一局部不断地优化; 在分布性上, 初始精英种子所在区域的解比较稠密, 在没有初始精英种子所在区域的解有的地方比较分散, 总体上接近pareto面. 而NSGA-II在前20代的实验结果看来, 都无法得到想要的结果, 只能得出随着代数的不断增大, 慢慢在逼近pareto面, 解的分布在每一处都较均匀.

对于ZDT2、ZDT3函数的2种方法的仿真结果如下:

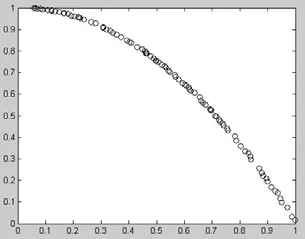
图7 基于精英种子策略的的多目标遗传算法(ZDT2)

图8 NSGA-Ⅱ算法(ZDT2)

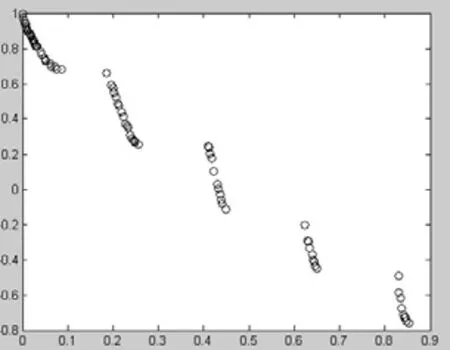
图9 基于精英种子策略的的多目标遗传算法(ZDT3)

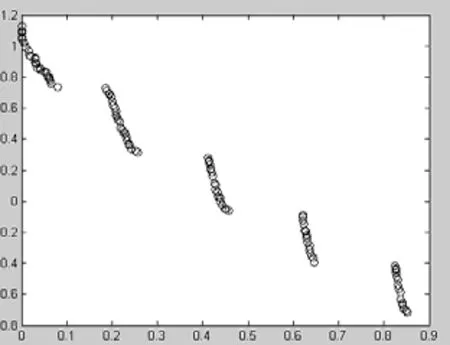
图10 NSGA-Ⅱ算法(ZDT3)

从上面的仿真结果可以看出, 引入的已知的最优解精英个体发挥了很好的作用, 它引导了进化过程中的寻优方向使得在已知信息的区域内产生了比较密集的Pareto解; 而且从最终优化的结果可以看出, 提出的算法既在已知信息区域内产生了大量的Pareto 解, 又在整个目标空间的前端产生了一系列分布比较均匀的Pareto解, 这样的好处是我们的算法能够以较快的速度收敛和较少的代数得到问题真正的Pareto解.

5 结论

本文提出的基于精英种子策略的多目标遗传算法既保证了优化问题能够收敛到真正的Pareto解, 又使得在进化过程中由于最优解精英个体信息的引入, 能够在已知信息区域内产生稠密的Pareto解来满足用户的需求. 本文只是利用了区间这个概念来描述用户的已知最优信息, 这对于比较具体的工程实践问题是完全可以的.

[1]Deb K, Pratap A, Agrawal S, Meyrivan T. A fast and elitist multi-objective genetic lgorithm: NSGA-II [J]. IEEE Trans. on Evolutionary Computation,2002, 6(2): 182～197

[2]孙即祥. 现代模式识别[ M]. 长沙: 国防科技大学出版社, 2003

[3]郑金华, 蒋 浩, 邝 达, 等. 用擂台赛法则构造多目标Pareto最优解集的方法[J]. 软件学报, 2007, 18(6): 1287～1297

[4]石 川, 李清勇, 史忠植. 一种快速的基于占优树的多目标进化算法[J]. 软件学报, 2007, 18(3): 505～516

[5]崔逊学, 林 闯. 一种基于偏好的多目标调和遗传算法[J]. 软件学报, 2005, 16(05): 761～770

[6]Jensen MT. Reducing the run-time complexity of multi-objective EAs: The NSGA-II and other algorithms [J]. IEEE Trans. on Evolutionary Computation, 2003,7(5): 503～515