悬臂式钻井平台悬臂梁振动特性研究＊

姜 伟

（中国海洋石油总公司）

悬臂式钻井平台悬臂梁振动特性研究＊

姜 伟

（中国海洋石油总公司）

根据海上悬臂式钻井平台的结构特点，结合海上作业的实际情况，考虑平台受到的均布载荷与集中载荷，建立了悬臂式钻井平台在作业状态条件下的力学模型，并推导出了悬臂梁挠曲方程和振动频率求解方程。通过算例，分析了悬臂梁外伸距离、甲板质量、井深等对钻井平台振动频率的影响规律。本文研究结果对提高井口及井下工具作业安全有指导意义。

悬臂式钻井平台 均布载荷 集中载荷 悬臂梁振动频率

1 问题的提出

悬臂式钻井平台具有良好的井口覆盖特性，已在海上油田开发井钻井作业中得到越来越广泛的应用。由于悬臂式钻机可以很方便地调整钻台转盘的位置，通过调整悬臂梁的外伸距离以及在上层钻台滑轨的移动，实现在钻井平台主龙骨中心线以及正交方向线这两个方向的移动，从而很方便地在一个插桩位置通过正交两个方向的移动，达到调整井口位置和多钻丛式生产井的目的，这种方式在海上丛式生产井钻井作业中发挥了重要的作用。

然而，随着悬臂式钻井平台大量的使用，也发现了一些问题，特别是使用悬臂式钻机后，随着钻机大钩负荷的变化，在钻台一端的钻台平面有明显的上下运动，有时当大钩负荷变化幅度较大时全平台都有明显摇晃的感觉，有时钻具对井口耐磨补心的磨损加剧，有时感到钻杆有明显的偏磨[1－2]。据笔者多年的分析和观察认为，这些问题与悬臂梁本身的运动特点有一定的关系，因此从机理上对悬臂梁的振动特性进行深入的系统分析和研究，对于指导今后的钻井工作以及保证井下工具的安全和钻井工作的顺利进行具有十分重要的意义。

2 悬臂梁受力模型的建立

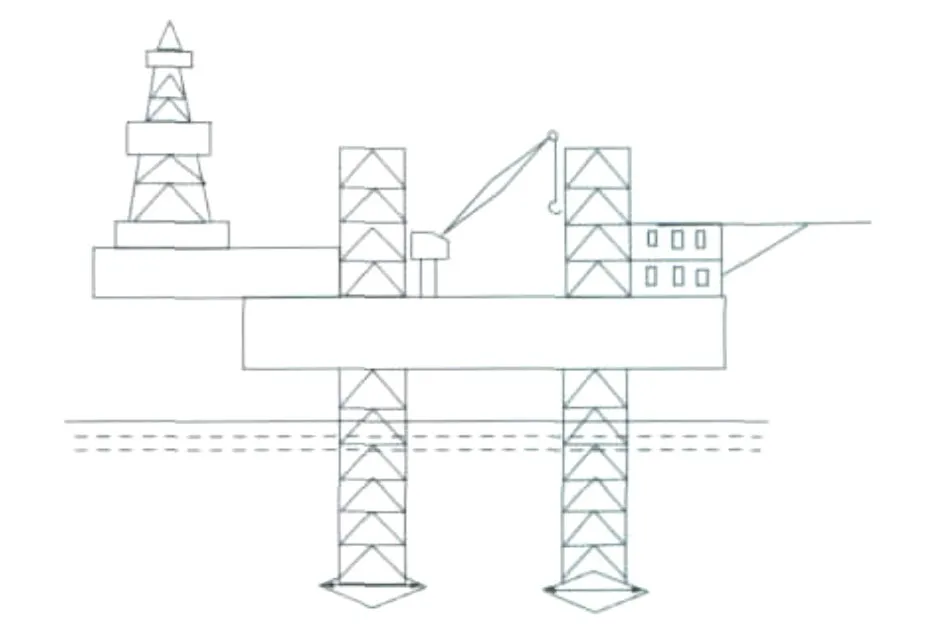
图1 悬臂式钻井平台示意图

海上自升式悬臂梁钻井平台如图1所示，它的钻井绞车置于悬臂梁上，悬臂梁可以在主甲板的滑轨上根据井口不同位置实现在主龙骨方向上的滑动和在下底座的滑动来对准井口，满足钻井作业的需要。以悬臂梁为研究对象，沿悬臂梁滑轨的运动方向建立坐标系的横向x轴，沿大钩运动方向建立坐标系的纵向y轴，悬臂梁受力模型如图2所示。为了便于研究，首先作如下假设：

图2 悬臂梁受力模型

（1）悬臂梁滑移靴为支点A，视为滑动支撑，井槽船舷边为支点B，视为固定支撑；

（2）在悬臂梁甲板上，堆放着钻柱和套管等物品，其重量可视为载荷q；

（3）在钻井绞车上，大钩受到钻具的拉力，即视为悬臂梁受到的集中作业力p，此力作用在外伸梁的C端；

（4）钻井平台升船后处于稳定工作状态，因此可以忽略钻井平台受到的水平方向上的风和流的载荷影响。

由文献[3]可知

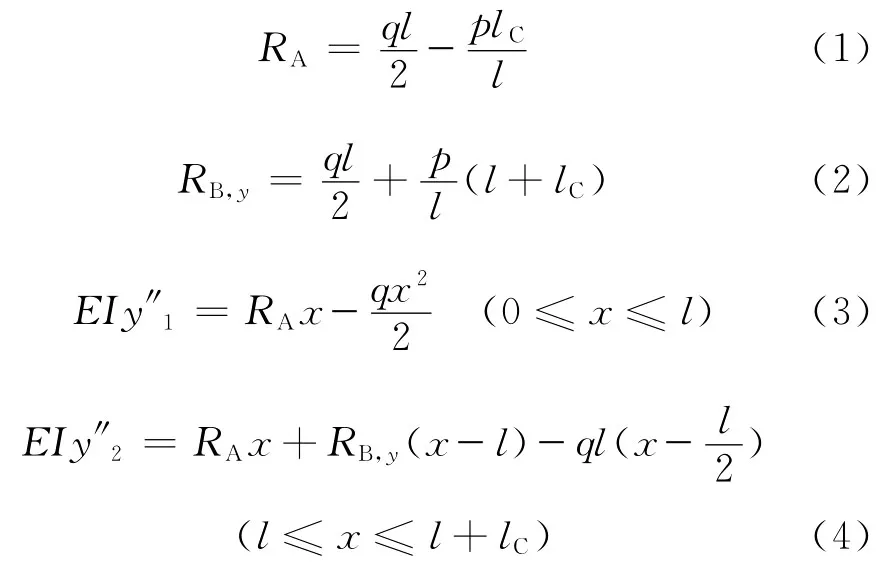
由式（3）、（4）得

由式（5）、（6）得

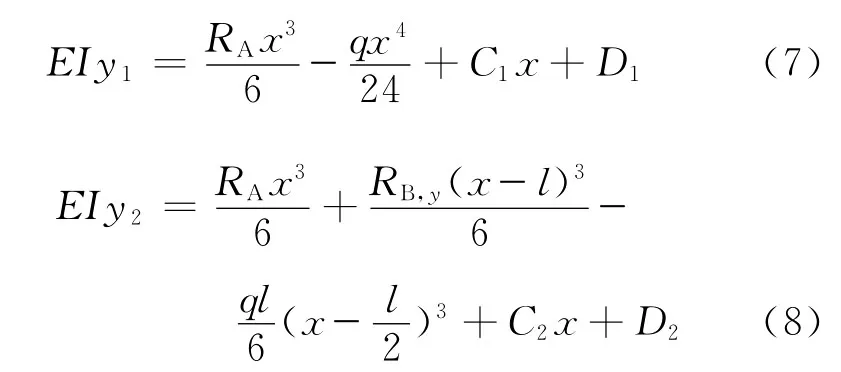
由边界条件

（1）当x＝0，y1＝0，由式（7）可得

（2）当x＝l，y1＝0，由式（1）、（7）可得

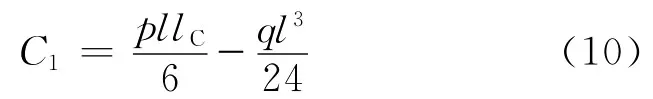
（3）当x＝l，y2＝0，由式（8）可得

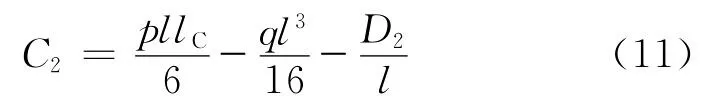
由式（5）可知，当x＝0时，得到A处转角θA

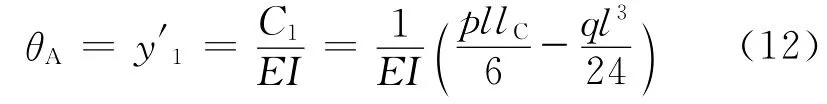
B支点处右边转角

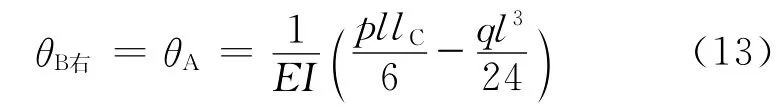
当x＝l时，由方程（6）可知

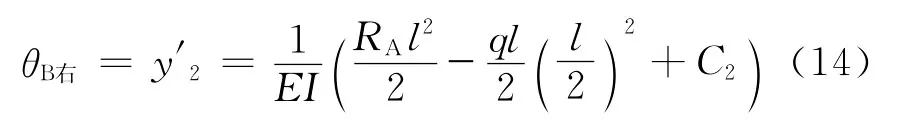
由式（1）、（13）、（14）得

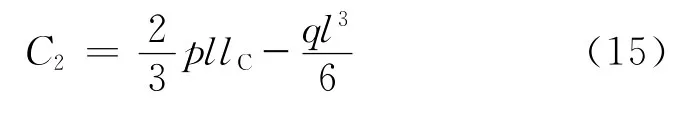
联立式（11）、（15）可得

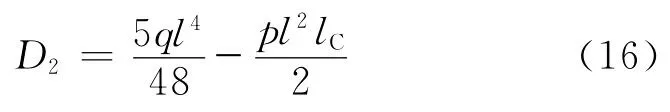
至此得到挠曲方程

对方程式的讨论：

（1）当q＝0，x＝l＋lC时，由式（18）可知

式（19）形式同文献[3]一致。

（2）当q＝0时，由式（17）可得

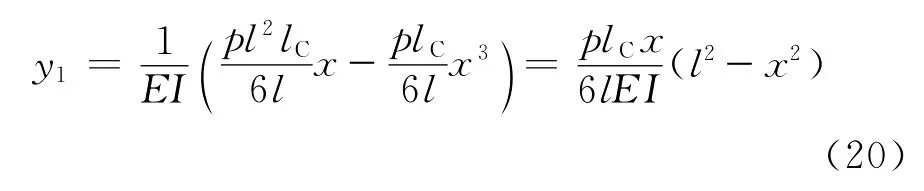
式（20）形式同文献[4]一致。

（3）当q＝0，x＝l＋lC，由式（18）可得

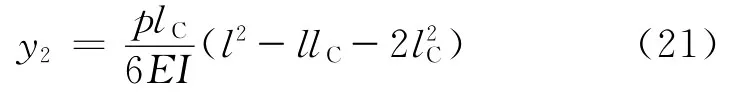
3 悬臂梁振动频率的计算方法

有文献[5]可知，在机械能守恒定律的基础上，采用瑞利法可以进行悬臂梁振动频率的近似计算，并且这种方法在工程上也很适用。在均布载荷和集中载荷共同作用条件下，由文献[5]可知，悬臂梁振动频率为

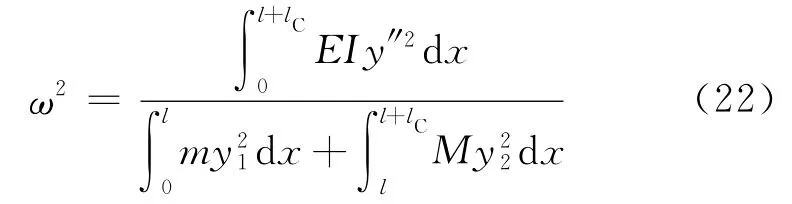
由式（17）可得

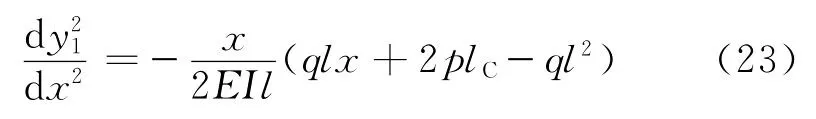
由式（18）可得

将式（23）、（24）和式（17）、（18）代入式（22），可以得到悬臂梁振动频率方程为

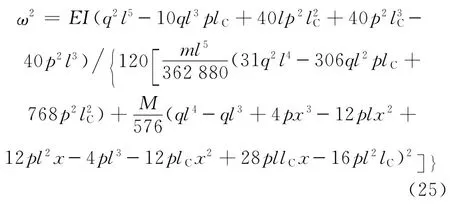
为简化和方便起见，令

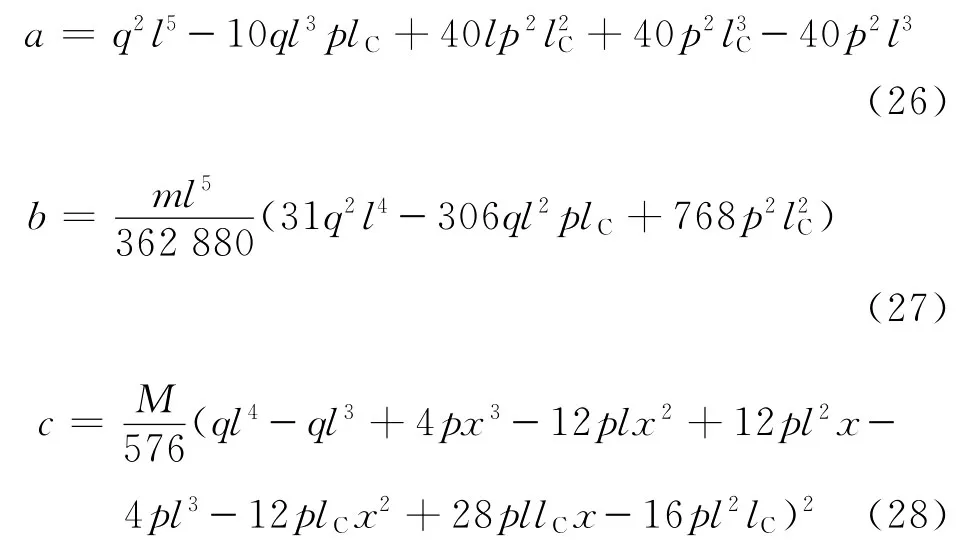
则

再将悬臂梁的振动频率ω折算成钻柱的转速Nn，由文献[6]可知

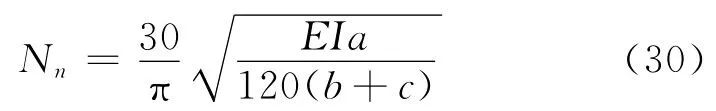
至此不但建立了悬臂梁的挠曲变形方程，同时还通过瑞利法求解了悬臂梁的振动频率方程，并且还导出了与钻柱转速之间的关系。观察式（25）可以发现，悬臂梁的振动频率与其它参数之间的关系为：

（1）悬臂梁振动频率与梁的抗弯模量EI成正比，并且是平方根的关系；

（2）悬臂梁振动频率与甲板上均布载荷质量m成反比，即均布载荷质量越大，振动频率越低；

（3）悬臂梁振动频率与井架下底座集中载荷质量M成反比，即集中载荷质量越大，振动频率越低。

4 实例计算

以渤海10号自升式悬臂梁钻机为例，该平台悬臂梁可以移动的前后距离为0～12.19 m，左右可以移动0～3.66 m。由于悬臂梁是一个很大的形状复杂的组合形体，如果直接计算其轴惯性矩，不但计算繁杂而且也很难准确计算，因此利用悬臂梁的负荷实验来求解。由在船厂进行的实验数据可知，在大钩负荷2222.64 k N时，测得悬臂梁端点挠度见表1。

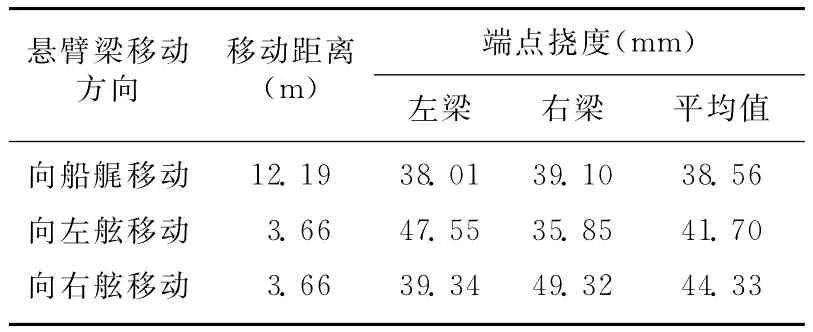
表1 悬臂梁端点挠度测定值

在实验条件下，悬臂梁甲板上无钻柱重量，因此此时q＝0，仅受集中载荷p的作用，由式（19）可知，此时端点挠度为

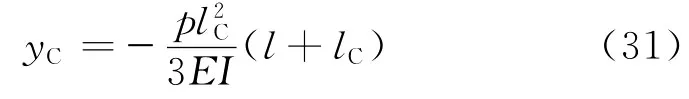
根据式（31）可求得抗弯模量EI。

例1。已知采用渤海10号自升式悬臂梁钻井平台在渤海某油田钻井，井深为2000 m，采用钻具组合为：φ203.2 mm钻铤100 m（线质量220 kg/m）＋φ127 mm加重钻杆×2000 m（线质量72 kg/m）＋φ127 mm钻杆×1700 m（线质量29 kg/m），钻压为200 k N，大钩载荷为660 k N，求悬臂梁在不同外伸位置时的振动频率。

解：设工作条件下下甲板载荷质量为2.5～160 t之间随井深增量增加变化，则由已知条件和式（17）、（18）、（26）～（31）求得悬臂梁振动频率计算结果见表2～4。

观察表2～4，可以发现以下特点：

（1）当悬臂梁从8.19 m推向12.19 m的过程中，其振动频率随伸出的距离成正比，如表2中主龙骨中心线上，悬臂梁外伸至8.19 m，当其悬臂甲板上均布载荷质量m为5 t时，其振动频率为5.20 s－1，而悬臂梁外伸至12.19 m时，在同样条件下其振动频率达到41.12 s－1，增加了近7倍；

（2）在同样的外伸距离时，随着甲板上均布载荷质量m的增加，振动频率呈减小的变化，如表2中悬臂梁外伸至12.19 m，当其甲板上均布载荷质量m由2.5 t增加至160 t时，其振动频率则由 57.81 s－1降 低 至 7.31 s－1，降 低 了 近7/8；

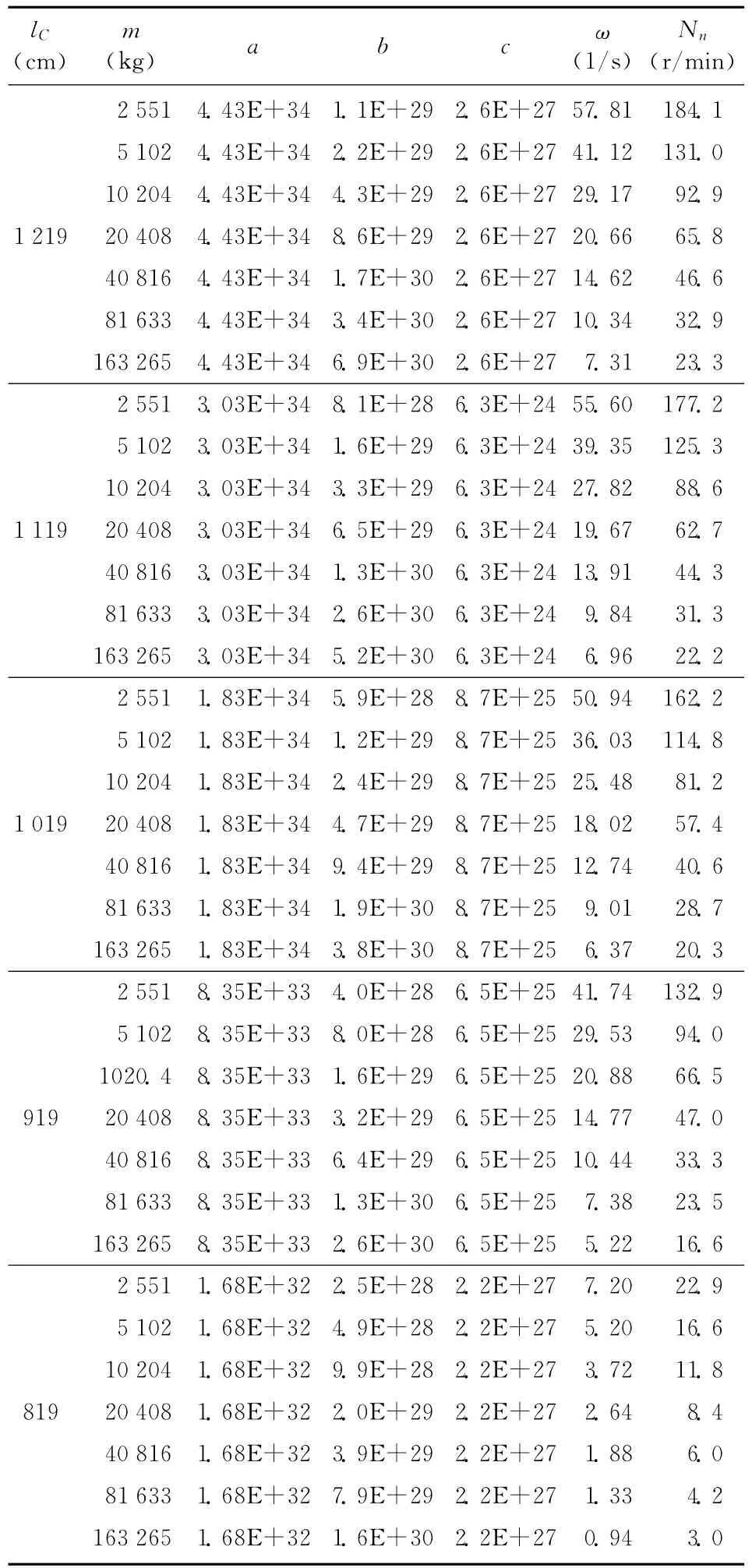
表2 沿悬臂梁主龙骨中心线移动时的振动频率和转速分布

（3）钻机向悬臂梁的左舷或右舷移动时，其振动频率的变化规律同前面一致，所不同的是在左舷时的振动频率略高于在右舷时的振动频率。

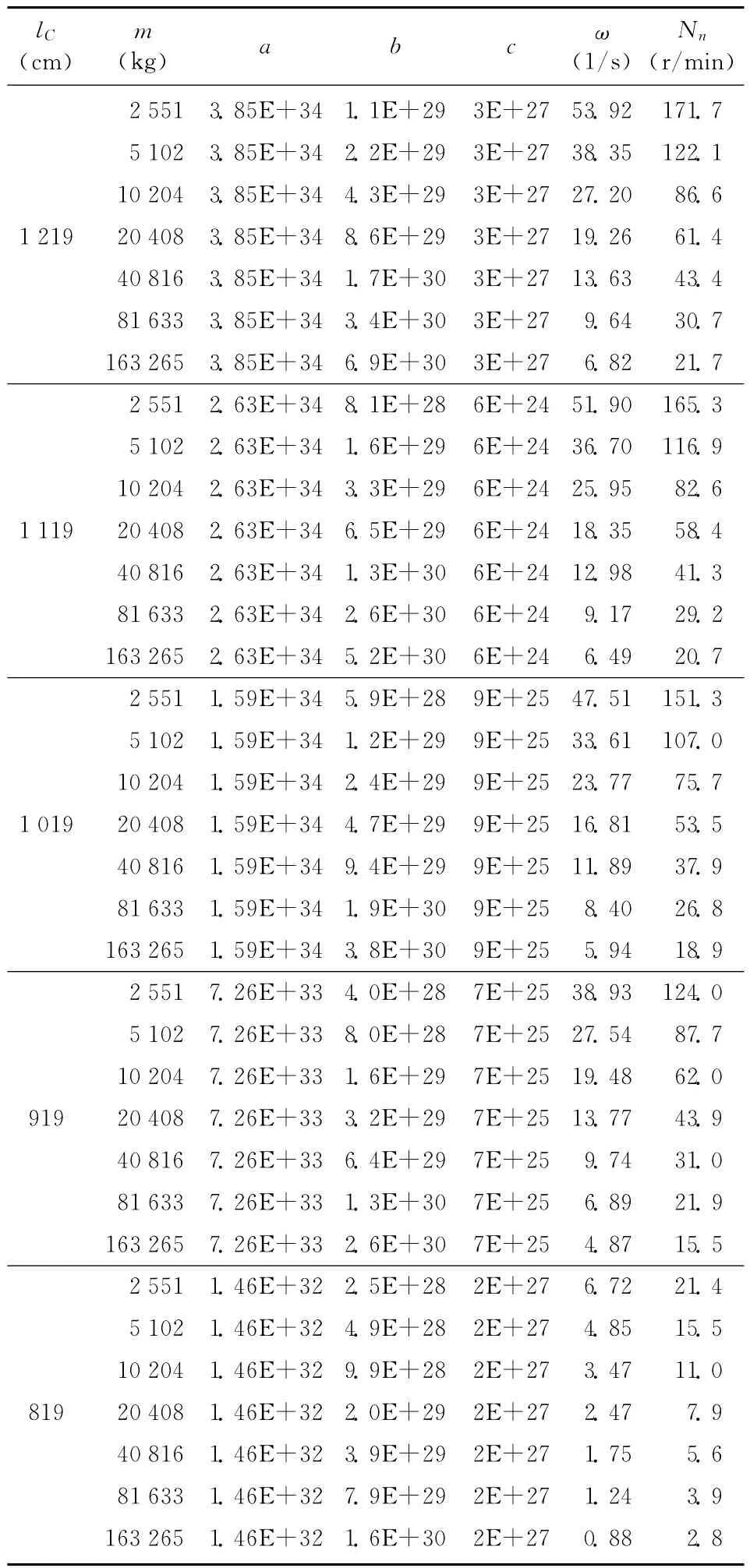
表3 悬臂梁向右弦移动时的振动频率和转速分布

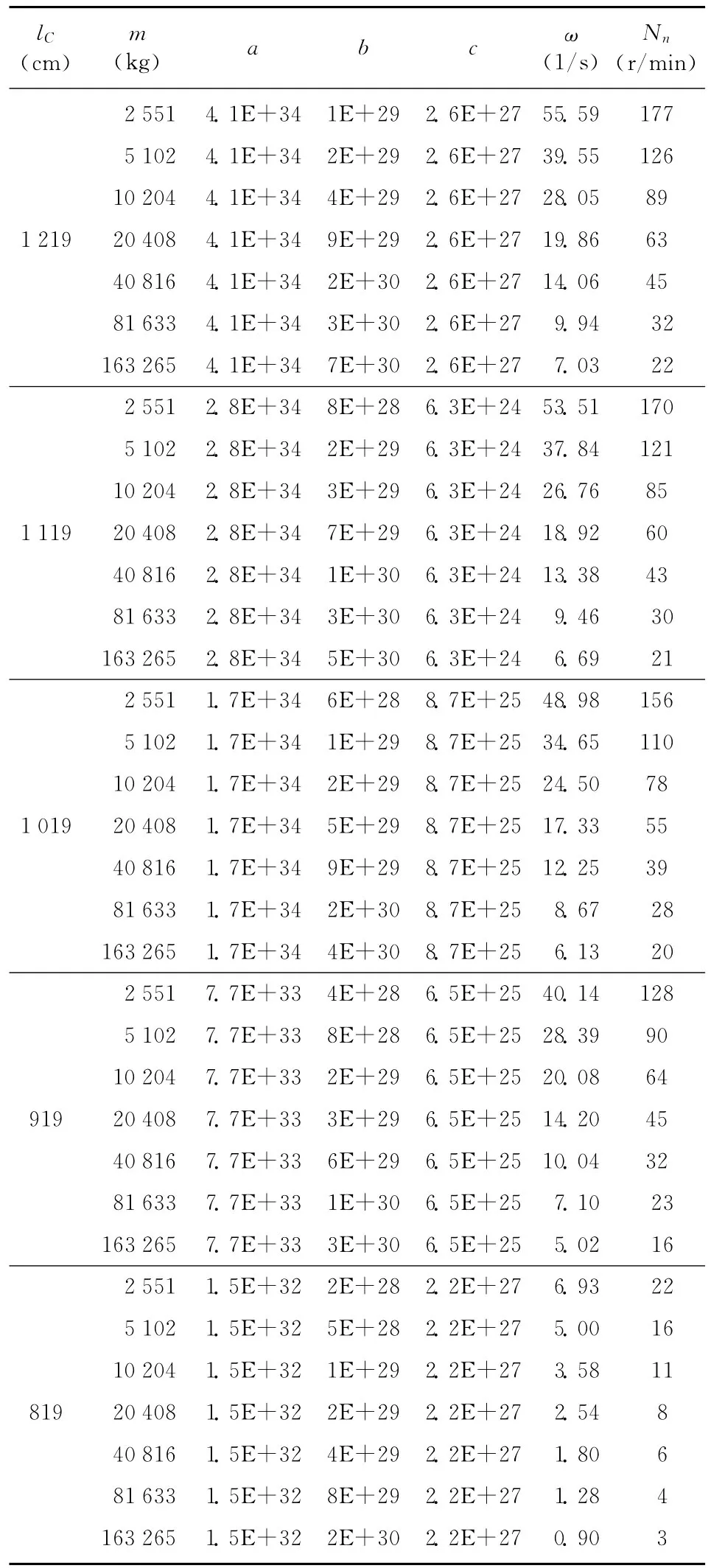
表4 悬臂梁向左弦移动时的振动频率和转速分布

例2。已知条件如例1，改变井深为3000 m，此时大钩钩载为950 k N，求悬臂梁振动频率。

解：同例1的解题方法，求得悬臂梁振动频率计算结果见表5～7。

观察表5～7，并结合表2～4，可以发现：

（1）井深3000 m时，悬臂梁的振动特性变化规律与井深2000 m时完全一致；

（2）井深增加了1000 m，大钩负荷增加至950 k N，相同位置时悬臂梁振动频率都略有降低，如在井深3000 m时，当悬臂梁外伸12.19 m时，甲板上均布载荷质量2.5 t，其振动频率为51.25 s－1，而在井深2000 m时，同样条件下其振动频率为57.81 s－1，大约降低了11%。

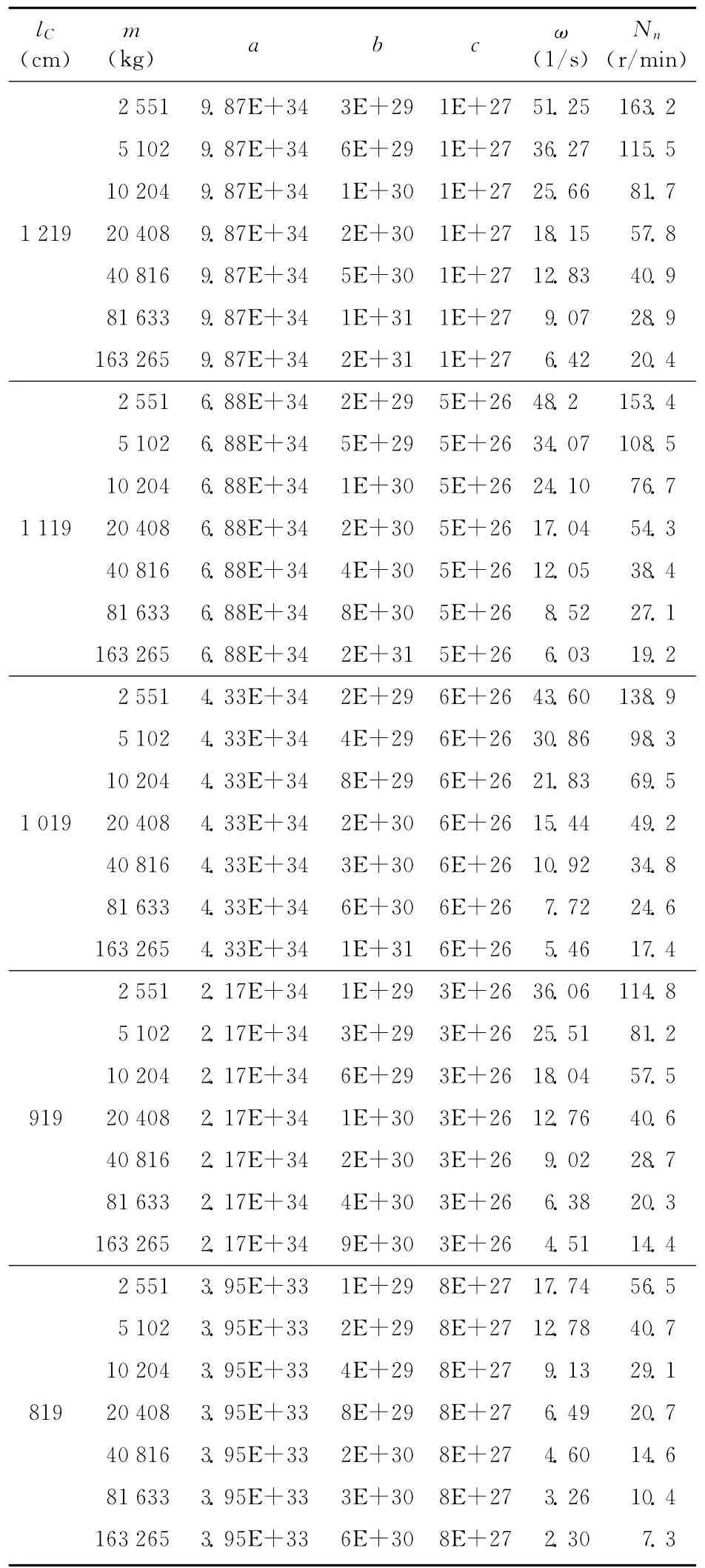
表5 悬臂梁沿主龙骨中心线移动时的振动频率和转速分布

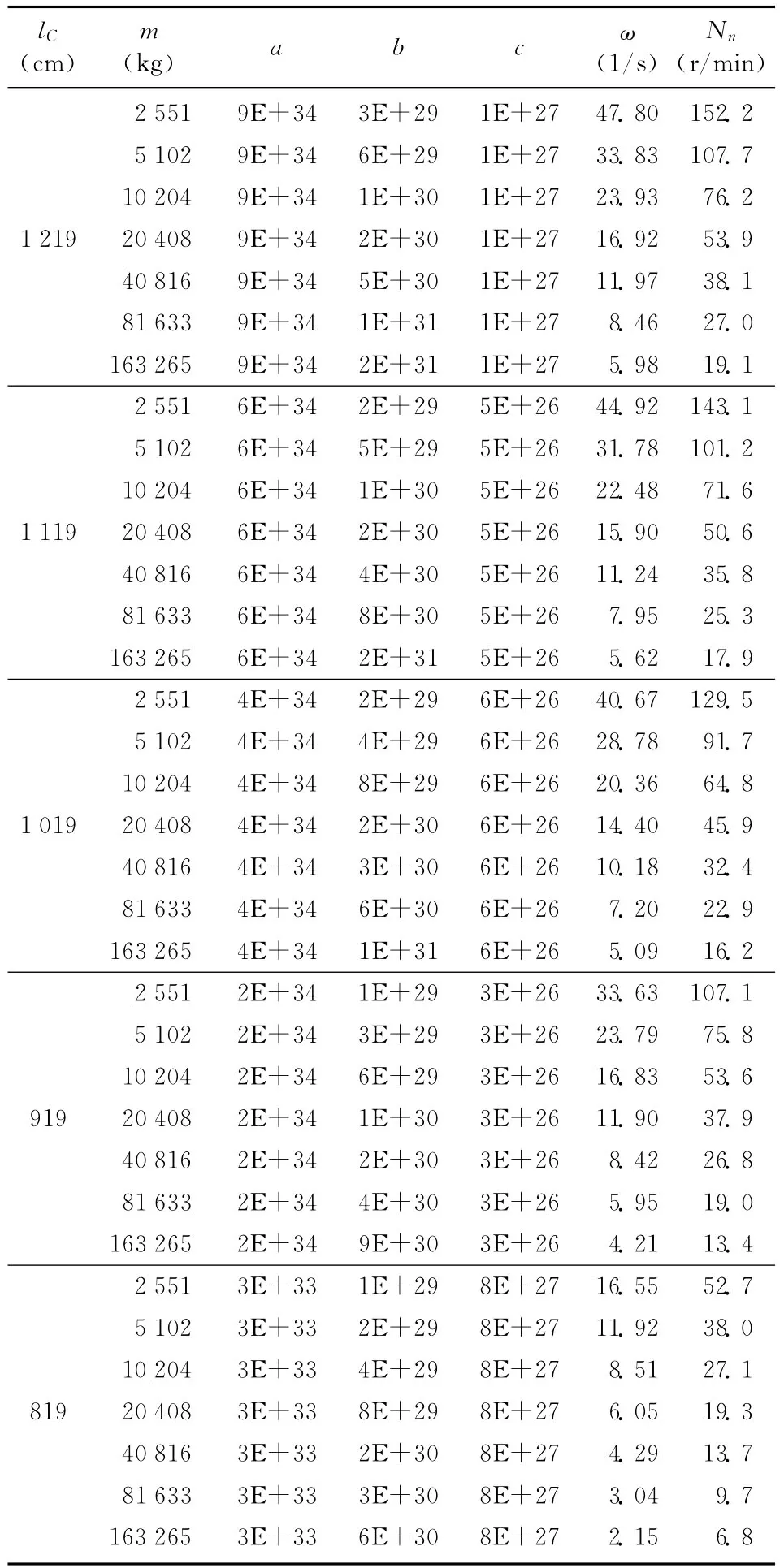
表6 悬臂梁向右弦移动时的振动频率和转速分布

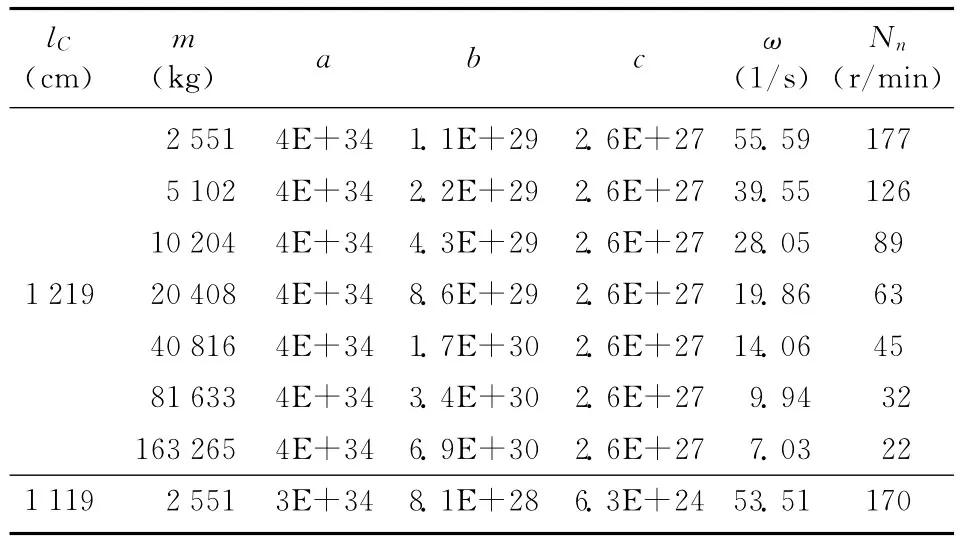
表7 悬臂梁向左弦移动时的振动频率和转速分布

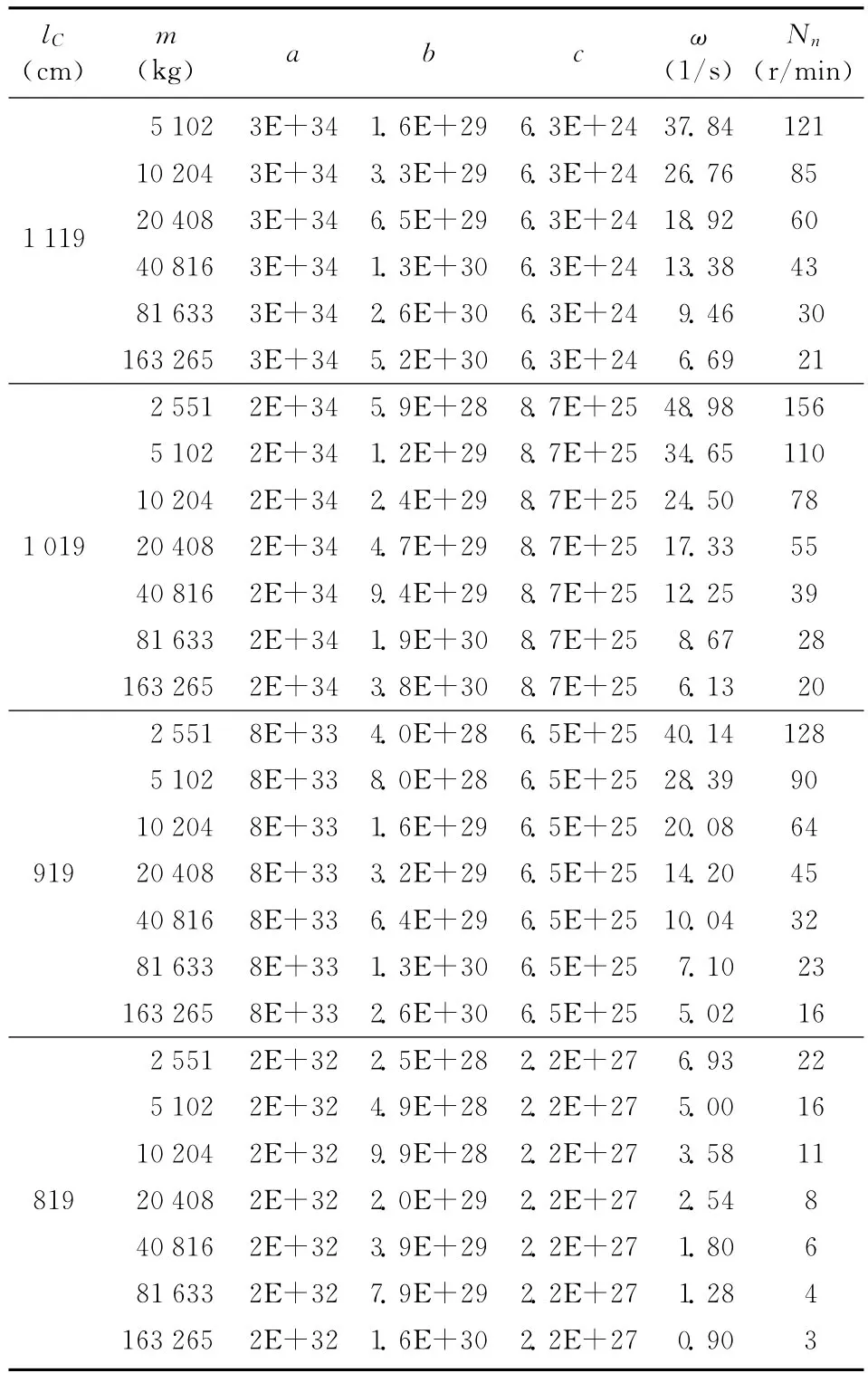
表7 悬臂梁向左弦移动时的振动频率和转速分布（续表）

5 结论

（1）本文利用建立外伸梁受均布载荷和集中载荷条件下弹性变形的挠曲方程将悬臂式钻井平台的载荷特性与瑞利法结合起来，用以计算悬臂梁的振动频率，基本反映了现场悬臂钻机的使用情况，方法简单可行，具有一定的合理性，对钻柱转速选择有指导意义。

（2）算例计算表明：随着悬臂梁外伸距离增加，悬臂梁振动频率增大；随着甲板上均布载荷质量的增加，悬臂梁振动频率降低；随着井深增加，悬臂梁振动频率降低。

符号注释

E—钢材的弹性模量，通常E＝210 GPa；

I—轴惯性矩，m4；

q—悬臂梁均布载荷，k N/m；

p—大钩，集中载荷k N；

l—悬臂梁两端支点距离，m；

lC—悬臂梁外伸距离，m；

m—悬臂梁甲板上均布载荷的质量，kg；

M—井架下底座载荷的质量，kg；

RA、RB，y—悬臂梁A、B 支点处的垂向约束力，k N；

y1、y2—悬臂梁AB、BC段上的挠度，m。

[1] 姜伟.悬臂式钻井装置载荷特性对钻井设计和施工的影响[J].中国海上油气（工程），1993，5（6）：9－14.

[2] 姜伟.悬臂式钻井装置振动特性对开窗作业的影响[J].中国海上油气（工程），1994，6（2）：34－39.

[3] 刘鸿文主编.材料力学[M].北京：人民教育出版社，1979.

[4] 李廉锟主编.结构力学[M].北京：人民教育出版社，1979.

[5] 清华大学工程力学系固体力学教研组振动组.机械振动[M].上册.北京：机械工业出版社，1980.

[6] 姜伟.海洋石油钻井工程力学研究与实践[M].北京：石油工业出版社，2008.

Study on vibration characteristics of cantilever beam of cantilever drilling platform

Jiang Wei
（CNOOC，Beijing，100010）

According to the structural feature of offshore cantilever drilling platform，the mechanical model is built considering the uniformly distributed load and point load and associating with actual offshore operation.And the bending flexure equation and vibration frequency equation of cantilever beam are also derived.The influence of cantilever overhanging distance，deck mass and well depth on the vibration frequency of the platform is analyzed through the case calculation.The study results are significant for improving the safety of well head and down hole operations.

cantilever drilling platform；uniformly distributed load；point load；vibration frequency

＊国家“十二五”重大专项“海上稠油高效开发示范工程（编号：2011ZX05057）”部分研究成果。

姜伟，男，高级工程师，1982年毕业于原西南石油学院钻井工程专业，现任中国海洋石油总公司副总工程师（钻井）。地址：北京市东城区朝阳门北大街25号海洋石油大厦（邮编：100010）。

2011－06－24

（编辑：孙丰成）