模糊C均值聚类算法的改进研究

,,

(安徽科技学院 理学院,安徽 风阳 233100)

0 引言

随着计算机、通信和网络技术的发展,人们被海量信息淹没的同时又面临着知识的贫乏,因此,开始思考采用一定的方法从蕴含着丰富信息的数据中抽取感兴趣的知识和信息,包括有效的、新颖的、潜在有用的概念、规律和模式等,这就是数据挖掘．在数据挖掘技术中,聚类分析是其中最主要的研究课题之一,其主要功能是根据对象的属性,将大规模的数据集合分为由类似的对象组成的多个类．其中,类内具有最大的相似性,类间具有最小的相似性．

目前,常用的聚类分析方法有划分的方法、层次的方法、基于密度的方法、基于网格的方法、基于模型的方法和模糊聚类方法．由于在现实生活中,很多对象没有严格的属性,不能把它绝对的划分到某个类别中,因此,模糊聚类分析成为聚类的研究主流,它得到的是样本属于某个类别的不确定程度,更能客观的反映真实的世界．模糊C均值聚类算法(FCM)是一种代表性的模糊聚类算法[1,2],但是FCM还有很多缺陷和不足,其中最主要的就是算法的性能依赖于初始中心的选择,选取不同的初始中心,会得到不同的聚类结果,影响到聚类的稳定性和准确率．针对上述问题,我们首先对要聚类的数据采用数据分区技术进行预处理,然后根据物质质心的定义及质心运动原理,计算每个数据分区的质心做为FCM聚类的初始聚类中心,降低FCM对初始中心的依赖性．

1 经典FCM算法

在非监督模式识别领域,FCM聚类算法是应用最广泛的算法之一．Dunn在Ruspini提出模糊划分概念的基础上,改进传统的硬C均值聚类算法,把其推广到模糊情形,形成FCM算法．Bezdek在其提出的FCM算法的基础上推广到更一般的形式,就形成了我们今天所看到的经典FCM算法．经典FCM算法的基本思想是:随机初始化若干个聚类中心,计算样本中的每个数据对聚类中心的隶属度,构成隶属度矩阵,然后通过若干次的迭代更新聚类中心和隶属度矩阵,使目标函数值达到最小．目标函数如下:

(1)

假设待聚类数据集合X中含有n个对象,其中,m是模糊加权指数,控制算法的柔性,m>1;c表示分类数;uij∈[0,1]表示第i个样本点xi属于第j个分类的隶属度;dij表示样本点xi与聚类中心vj的欧几里德距离;V={vi}(i=1,2,…,c)表示聚类中心矩阵,U={uij}表示隶属度矩阵,其中隶属度值uij具有如下的约束条件:

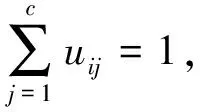
(2)

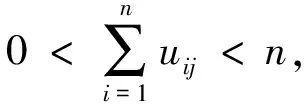
(3)

在迭代求Jm(U,V)最小值过程中,可通过(4)、(5)不断的更新隶属度和聚类中心矩阵．

隶属度更新公式为:

(4)

聚类中心更新公式为:

(5)

2 改进FCM算法

2.1 数据分区

在海量高维数据中,统计数据在每一维上的分布特性,根据它的分布特性,可将数据划分为若干个分布均匀的区域[3-5]．划分的基本过程如下:首先,从采集的大量数据中选取一个子数据集做为样本数据．然后,用直方图分析子数据集中每一维上的分布密度．直方图是表示数据分布变化情况的一种统计工具,是由若干个高度不等的矩形组成,横轴表示数据类型,纵轴表示分布情况．绘制直方图之前,要统计数据点中的最大值和最小值,根据数据的特点决定组数并利用每组中两个端点的差值求出组距．最后,绘制直方图,得到的直方图的类型有双峰型、偏态型、折齿型等,通过分析结果,决定在那一维上分区、划分为几个区及各分区的边界．

2.2 质心计算

定义1 数据点邻域[6]:设置距离阈值σ,数据集中与数据点的距离小于等于σ的对象组成的区域为该数据点的邻域．

定义2 数据点质量[7]:数据点在σ邻域内所包含的对象的个数为该数据点的质量．

定义3 数据分区内的质心:假设划分的数据分区为D维空间中N个数据点组成的系统,在物理学中忽略其体积,只考虑数据点质量,定义质量中心为系统的质心,质心和质心位置矢量的计算公式为:

(6)

(7)

其中,mi和ri分别为该数据分区内第i个数据点的质量和位置矢量,M和R分别为整个系统的质心及质心位置矢量．对于三维空间中的数据分区,其维度分别为x,y,z,第i个数据点坐标为(xi,yi,zi),则质心的坐标为:

(8)

2.3 改进后的算法流程

在数据分区和质心运动原理的基础上,改进后的FCM算法流程如下:

步骤1: 根据样本数据集中某一维的直方图进行数据分区,分区个数c既为聚类类别数,设置一个足够小的正数ε;

步骤2: 用式(6)、(7)、(8)计算每个数据分区的质心坐标和质量形成初始聚类中心集合V;

步骤3: 用式(4)计算或更新划分矩阵U;

步骤4: 用式(5)更新聚类中心V;

步骤6: 输出隶属度矩阵U和聚类中心矩阵V．

3 实验分析

为了测试改进算法的有效性,我们在Matlab6.5平台的基础上,采用数据挖掘研究院网站提供的某校园网日志记录进行仿真实验．截取子数据集共812条日志记录,经过数据预处理后得到8个用户U={U1,U2,U3,U4,U5,U6,U7,U8}对该校园网6个页面P={P1,P2,P3,P4,P5,P6}的访问次数统计矩阵,为了进行用户聚类,把相似浏览行为的用户聚成放在一起,对该矩阵数据进行标准化处理,即用户访问某个页面的次数除以访问该网站所有页面的总次数,得到如下的矩阵:

根据上述矩阵,统计各维度上的直方图(图1),得到P1维度上的分布出现两个密集区,而且相对分布比较均匀,符合我们分区的要求,因此在P1维上把数据集分为3个区,也就是把用户初步分为3类．

在上述分区的基础上,计算每个分区的质心及质心位置矢量,然后再应用FCM算法进行聚类,下面给出直接进行FCM聚类和数据分区及计算质心后再进行FCM聚类后的性能比较．通过表1我们可以看出计算分区质心后,降低了迭代次数和运行时间．

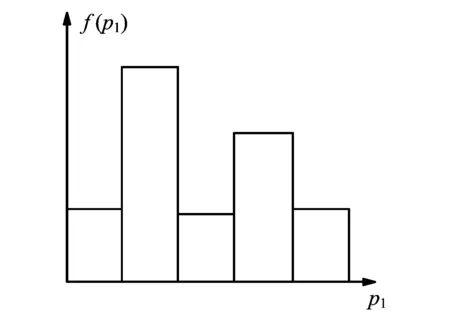
图1 P1维上数据分布直方图

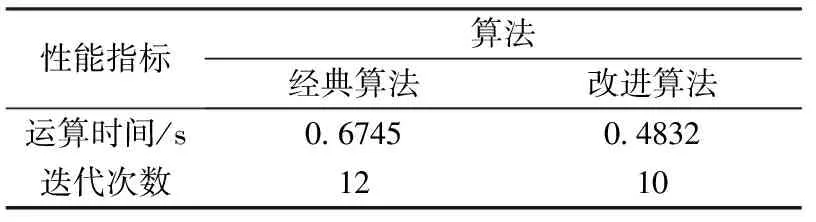
表1 两种 FCM算法的性能比较

4 结束语

FCM目前被广泛的应用到Web挖掘,图像处理,模式识别等研究领域,引起了人们的广泛关注．针对FCM对初始聚类中心依赖性比较强这一缺陷,本文在数据分区和质心计算的基础上,粗略的确定分类数,计算的初始质心接近实际的类中心,因此降低了迭代次数和运行时间,得到比较稳定的聚类结果,体现了改进的FCM的优越性.

[1]江克勤.优化初始中心的模糊C-均值算法[J].合肥工业大学学报,2009,32(5):762-768.

[2]张慧哲,王坚.基于初始聚类中心选取的改进FCM聚类算法[J].计算机科学,2009,36(6): 206-209.

[3]郑洪英.大规模数据集聚类中的数据分区及应用研究[J].计算机应用研究,2007,2(2):203-205.

[4]何中胜,刘宗田,庄燕滨.基于数据分区的并行DBSCAN算法[J].小型微型计算机系统.2006,27(1):114-116.

[5]王鑫,王洪国.基于数据分区的最近邻优先聚类算法[J].计算机科学,2005,32(12):188-190.

[6]韦相,许海成,王红晓.网格质心运动的聚类初始化方法[J].计算机工程与应用,2010,46(13):135-138.

[7]汪永生,李均利.质心粒子群优化算法[J].计算机工程与应用,2011,47(3):34-37.