菱镁矿热分解微分方程的建立*

，，

(1.北京科技大学土木与环境工程学院, 北京 100083;2.中国科学院过程工程研究所生化工程国家重点实验室)

菱镁矿是一种以碳酸镁(MgCO3)为主要化学成分的天然矿物，是中国的优势矿产资源[1]，作为镁工业及耐火材料工业的主要原料[2- 3]可广泛应用于建材、化工、农牧业、造纸、航天航空、汽车及环保等行业[4]。对菱镁矿热分解的研究主要集中在热解的分解产物上, 而对其热分解动力学方面的研究较少。 菱镁矿热分解是制备镁单质及镁化合物的重要反应,因此研究其热分解过程和分解历程具有重要的意义。

热重分析(TG)具有简单、快速、准确等优点。将热失重曲线进行处理，可估算分解反应活化能，判断分解反应机理及影响因素，进而为化学反应动力学的理论研究提供依据[6]。笔者借助热分析仪和动力学分析法研究了菱镁矿热分解反应机理及其动力学模型。

1 实验

1.1 实验原料

实验选用辽宁海城菱镁矿为原料,其化学组成见表1。

表1 菱镁矿的化学组成 %

1.2 实验方法

采用氧化铝质坩埚，样品平均粒径为0.45 mm，样品质量为18.915 mg，氮气气氛,流量为75 mL/min，分别以15、20、25、35、40 ℃/min的升温速率将样品从25 ℃加热到900 ℃，使热分析曲线达到稳定状态。采用NETZSCH STA 449C综合热分析仪对试样进行TG-DSC分析。

2 结果与讨论

2.1 菱镁矿的热分解

图1为菱镁矿在不同升温速率下的TG-DSC曲线。

DSC曲线从上到下为15、20、25、35、40 ℃/min

由图1可知，菱镁矿热分解主要在400～800 ℃完成，与文献[7-8]的结果有些出入，这主要是由于测试条件、矿物结构和成分不同引起的。在程序升温过程中，不同升温速率的TG-DSC曲线变化趋势相同，DSC向下峰与TG曲线上的失重台阶相对应，且其失重率基本一致。DSC曲线出现向下峰是由于菱镁矿热分解需要吸收热量。TG曲线只有一个失重台阶，与之对应的是一个吸热峰，表明菱镁矿的热分解过程很可能属于一步反应。

2.2 动力学参数的计算

根据非等温反应动力学理论，得到线性升温条件下固相物分解反应动力学方程为[9-10]：

dα/dT=A/β·e-E/RT·f(α)

(1)

式中：T为反应温度，K；α为在温度T时的反应分解分数；f(α)为热分解动力学机理函数；A为频率因子，min-1；E为活化能，(kJ/mol-1)；β为线性升温速率，K/min。

求解动力学参数的方法都可以归结为对方程(1)的各种近似处理，实验采用Kissinger方程和Ozawa-Doyle方程，只需已知不同升温速率下的温度(Tm)，就可求得反应活化能，而不考虑其机理函数。Kissinger方程式如下：

(2)

由式(1)可知，作图可得到一条直线，从直线的斜率可以计算出活化能(Eα)，进而得到指前因子的对数lgA。 因此,只需在不同升温速率β下, 得到一组Tm, 即可计算其动力学参数Eα和指前因子(A)。Ozawa-Doyle方程如下：

lgβ=lg [AE/RG(α)]-2.315-(0.456 7E/RTm)

(3)

由式(3)可知，在反应机理函数G(α)相同时，lnβ与1/Tm呈线性关系，由不同的升温速率下的温度Tm,即可求得反应的活化能,而不必考虑其机理函数的具体形式。

根据式(2)、(3)结合图1中的DSC峰顶温度,计算得到菱镁矿热分解活化能和指前因子见表2。

表2 菱镁矿热分解反应动力学参数

2.3 微分方程的建立

为了从单条热重曲线对菱镁矿热分解反应非等温动力学进行研究，实验采用Coats-Redfern方程[11-12]如下：

ln [F(α)/T2]=ln [(AR/βE)-(E/RT)]

(4)

T2]对1/T作图应是一条直线。结合文献中常见的8个动力学模型函数[11-14]将实验数据代入相应的方程，分别进行多元线性回归。由线性相关系数R2可以判断机理函数的可靠程度, 动力学参数回归计算结果见表3。由表3可知，菱镁矿热分解过程线性相关系数R2较高且接近的机理函数为D3和3D，在相关系数接近的情况下，Malek法是进一步判断最概然机理函数的有效方法[15]。机理函数的标准曲线方程为：

y(α)=f(α)·F(α)/f(0.5)·F(0.5)

(4)

实验曲线方程为：

y(α)=(T/T0.5)2·[(dα/dt)/(dα/dt)0.5]

(5)

其中f(α)、F(α)为机理函数，dα/dt是由热重曲线得到。y(α)对α作图，若实验曲线与标准曲线重叠，或实验数据点全部落在某一标准曲线上，则判定该标准曲线所对应的f(α)或F(α)就是最概然的动力学机理函数。

以25 ℃/min为例，y(α)—α曲线见图2，其中实验曲线用虚线表示，并标为P。

由图2实验曲线和常用机理函数的标准曲线对比可以判定菱镁矿热分解属于D3机理，机理函数为：

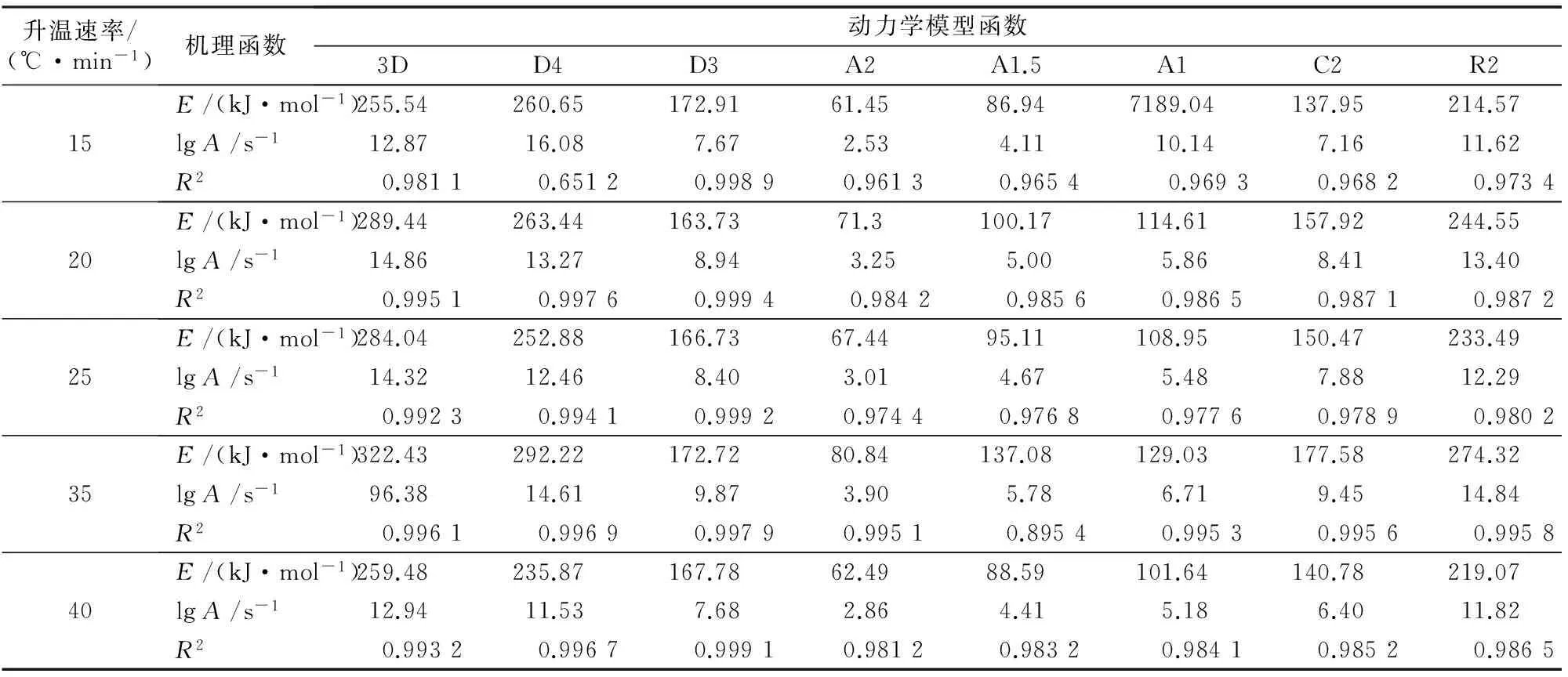
表3 动力学参数回归计算结果

图2 菱镁矿热分解y(α)-α曲线

F(α)=[1-(1-α)1/3]2

或f(α)=1.5(1-α)2/3[1-(1-α)1/3]-1

(6)

相应的动力学微分方程为：

dα/dt=

(108/β)exp(1-20 040.9/T)·{3/2(1+α)2/3[(1+α)1/3-1]-1}

(7)

2.4 比热容的计算

物质的比热容反映了物质在没有相变的情况下物质吸热或放热的能力。在热分析技术中，差热法(DSC)能直接测定物质在程序控温下所发生的热量变化，而且定量性及重复性都很好，因此受到普遍重视和应用，已成为最有力的热分析手段。且用DSC技术测定物质的比热容很直观。

图3为由DSC所测数据得到碳酸镁的比热容与温度的关系。由图3可知，碳酸镁的比热容随温度变化为光滑曲线，说明碳酸镁在室温下结构很稳定，可以长期保存。由最小二乘法拟合碳酸镁比热容随温度变化的多项式为：

Cp=-2.984 24×10-4+3.960 62×10-5T-5.438 5×10-7T2+3.664 62×10-9T3-1.283 95×10-11T4+2.273 66×10-14T5-1.593 4×10-17T6

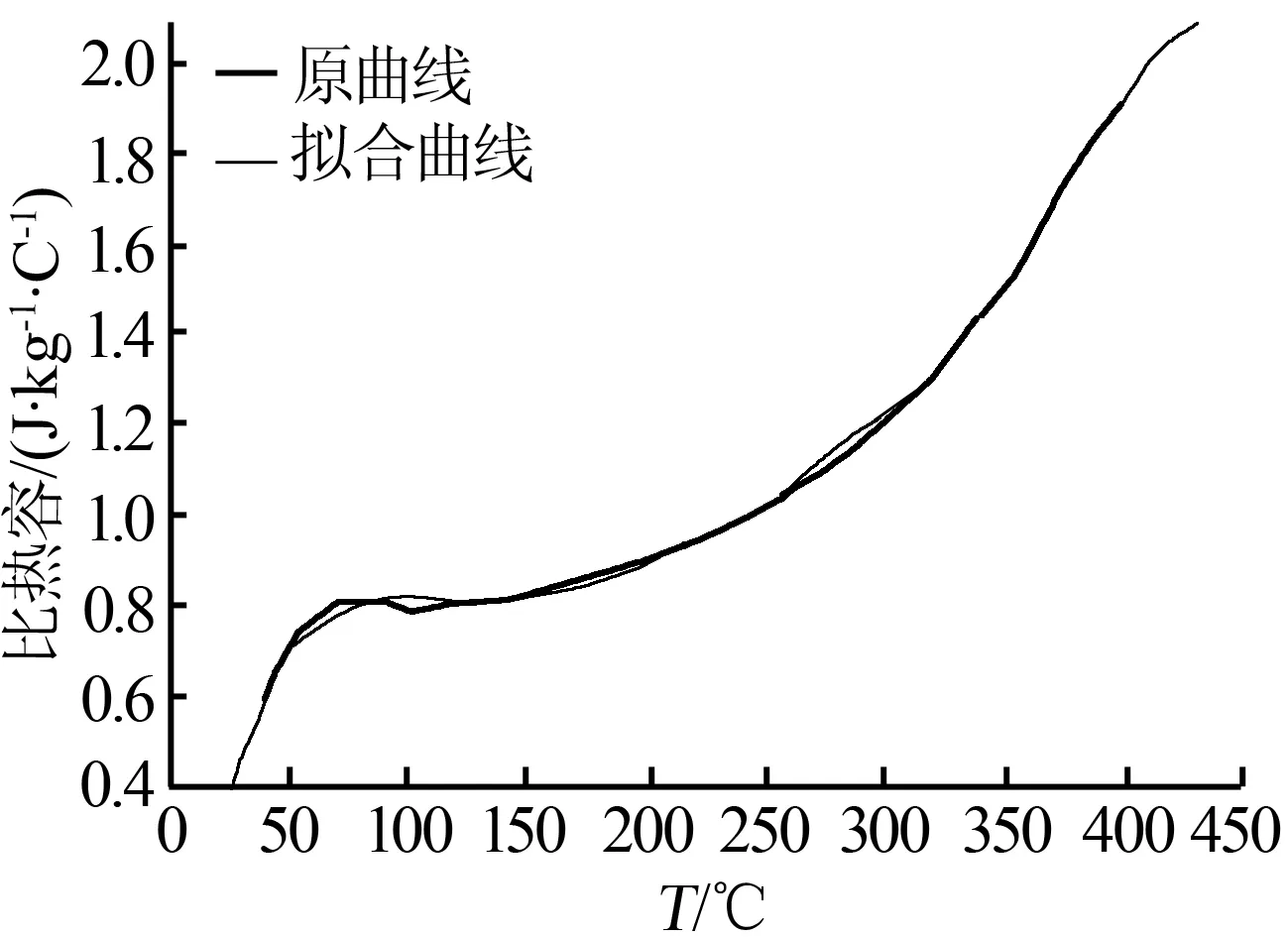
图3 MgCO3的比热与温度关系

3 结论

1)采用TG-DSC热分析技术对菱镁矿热分解过程进行了研究，得到菱镁矿的热分解为一步反应，分解反应的活化能和频率因子lgA分别为177.14 kJ/mol和7.39 s-1。

2)用Coats-Redfern方程和Malek法得出，菱镁矿热分解过程机理属于三维扩散控制步骤的D3机理，相应的动力学微分方程为dα/dt=(108/β)exp(1-20 040.9/T)·{3/2(1+α)2/3[(1+α)1/3-1]-1}。

3)根据DSC测试的数据，得到碳酸镁的比热容表达式为：Cp=-2.984 24×10-4+3.960 62×10-5T-5.438 5×10-7T2+3.664 62×10-9T3-1.283 95×10-11T4+2.273 66×10-14T5-1.593 4×10-17T6。

[1] Zhao Y N,Zhu G C.Thermal decomposition kinetics and mechanism of magnesium bicarbonate aqueous solution[J].Hydrometallurgy,2007,89(3):217-223.

[3] Fatih Demir,Bünyamin Dönmez.Optimization of the dissolution of magnesite in citric acid solutions[J].International Journal of Mineral Processing,2008,87(1):60-64.

[4] 王兆敏.中国菱镁矿现状与发展趋势[J].中国非金属矿工业导刊,2006,57(5):6-8.

[5] 沈玉芳,陈栋华,胡小安.热分析动力学处理方法现状及进展[J].中南民族大学学报：自然科学版,2002,21(3):11-15，29.

[6] 刘玉坤,朱玉,杨光,等.热重分析分级技术在配合物[Co(py)4Cl2](py=pydine)的热分解级动力学研究中的应用[J].云南大学学报：自然科学版,2005,27(5A):507-510.

[7] 刘镇海.热分析导论[M].北京:化学工业出版社,1991:249 -257.

[8] L′vov B V.Mechanism and kinetics of thermal decomposition of carbonates[J].Thermochimica Acta,2002(386):1-16.

[9] Niu S L,Han K H,Lu C M,et al.Thermogravimetric analysis of the relationship among calcium magnesium acetate, calcium acetate and magnesium acetate[J].Applied Energy,2010,87:2237-2242.

[10] Al-Othman Asma A,Al-Farhan Khalid A,Mahfouz Refaat M.Kinetics analysis of nonisothermal decomposition of (Mg5(CO3)4(OH)2·4H2O/5Cr2O3)crystalline mixture[J].Journal of King Saud University：Science,2009,21:133-143.

[11] Demir F,Donmez B,Okur H,et al.Calcination kinetic of magnesite from the thermogravimetric data[J].Institution of Chemical Engineers,2003,81:618-622.

[12] Lu C B,Song W L,Lin W G.Kinetics of biomass catalytic pyrolysis[J].Biotechnology Advances,2009,27:583-587.

[13] Samtain M,Dollimore D,Alexander K S.Comparison of dolomite decomposition kinetics with related carbonates and the effect of procedural variables on its kinetics parameters[J].Thermochimica Acta,2002,392-393:135-145.

[14] 郑瑛, 陈小华,周英彪,等.CaCO3分解机理和动力学参数的研究[J].华中科技大学学报:自然科学版,2002,30(12):86-88.

[15] 胡荣祖,史启枕.热分析动力学[M].2版.北京:科学出版社，2001.149-150.