基于ECC的存在特权集的门限群签名方案

董玉蓉

（贵州大学 计算机科学与信息学院，贵州 贵阳 520025）

基于ECC的存在特权集的门限群签名方案

董玉蓉

（贵州大学 计算机科学与信息学院，贵州 贵阳 520025）

通过对一种ElGamal类型存在特权集的门限群签名方案的分析研究,提出了一种基于ECC的存在特权集的门限群签名方案。该方案能有效防止KDC的欺诈,且只有在同时满足（t，n）和（t1，n1）门限签名时才能生成消息的有效签名，从而实现了门限特性，并具有门限群签名应有的性质。

特权集；秘密共享；门限群签名；ECC

群签名方案首次由Chanm和VanHeyst于1991年提出。在群签名方案中，允许每个成员都可以代表整个群体进行签名。在群签名方案中引入秘密共享，解决密钥安全与有效保管问题的同时也形成了一类新的群签名方案——门限群签名方案，即群体中的某些给定子集可以代表整个群体签名。在门限群签名方案中，门限群签名是由参加签名的各个成员所签署的部分数字签名按照某种方式结合后产生。2003年，BELLARE M等人提出了群签名的简化形式定义[1]。在这之后，不少学者提出的门限群签名方案均采用形式化的方法证明方案的安全性。参考文献[2]提出良好的门限群签名应该具备以下一些性质：群签名特性、门限特性、不可伪造性、验证简单性、匿名性、可追查性、强壮性。参考文献[3]中，Chen Feng等人基于Shamir秘密共享体制并结合 “存在特权集的门限群签名方案”的思想[4]，构造了一类基于离散对数问题的ElGamal类型的存在特权集的门限群签名方案。

本文利用椭圆曲线密码体制的特点对Chen Feng的方案进行改进。新的方案与原方案的共同点在于都使用双重秘密共享技术和单签名构造群签名的技术[3]，不同之处在于新方案实现了群成员的加入和撤销，提高了方案的通用性。同时，为了防止密钥分配中心的欺诈[5]，各用户对自己私钥的有效性进行了验证，并且利用椭圆曲线密码体制的特点优化本方案，进而提高了方案的效率和安全性。

1 一种ElGamal类型的存在特权集的门限群签名方案

Chen Feng依据离散对数问题提出了一种存在特权集的ElGamal类型门限群签名方案。

其基本设计流程如下：

（1）初始化：由可信的密钥认证中心KAC选取2个安全参数p、q，在有限域Fq上随机选取两个多项式 f（x）、g（x）,次数分别为（t-1）、（t1-1），并取有限域 Fq的本原元α。

（2）群密钥及秘密碎片的产生：群密钥d及群公钥z由KAC随机选取的两个多项式构成。利用“双重”SSS秘密共享方案为各签名者建立公私钥碎片。

（3）签名：群签名由参与签名的成员和签名服务机构SC共同生成：每个成员先生成自己的单签名，然后发送给SC验证该单签名是否为合法签名，再由SC决定是否接受；如果接受的单签名满足门限要求，则计算组合出群对消息的签名。

Chen Feng方案可简单描述为：在计算机网络开放式环境下，一个能够被完全信任的中心是不存在的。该方案的群密钥和群成员的秘密份额都由可信的密钥认证中心决定，不能保证密钥认证中心分发给各用户的密钥碎片有效，存在密钥分配中心欺诈的问题。此外方案没有考虑到群成员的安全有效的加入和撤销，因此不满足群签名的特性。

2 本文方案

本文提出的基于ECC的存在特权集的门限群签名方案共分为六个阶段：系统初始化、群密钥产生、群成员的加入和撤销、密钥分发、单个签名生成与验证、群签名生成。

2.1 系统初始化阶段

该方案的系统参数意义如下：

KDC：密钥分配中心；

Clerk：签名服务者，负责颁布签名；

G：由n个签名方组成的群体,至少有其中t方参与才可产生合法签名；

G1：G 的子集，有 n1（n1＜n）个成员。 至少有其中 t1（t1＜t）方参与才可产生合法签名，称为特权子集；

G2：G的子集，其中的签名方为普通用户；

ui：群成员 pi的公开身份；

IDi：群成员 pi的真实身份。

该方案的安全参数描述为：

（1）密钥分配中心KDC给定任一有限域Fp（p为大素数），并定义 Fp上的一条安全椭圆曲线 E（Fp），保证该椭圆曲线的离散对数问题是难解的。在E（Fp）上选一基点P，其阶数为 q（q为一个大于 160 bit的大素数）。另外，KDC还选择一个单向安全的Hash函数H（）。

（2）KDC构造 2个秘密多项式 f（x）∈RFq[x]，g（x）∈RFq[x]，次数分别为（t-1）和（t1-1）。

其 中 ，a0=f（0），b0=g（0），ai，bj∈Zq*（i=1，2，… ，t-1；j=1，2，…，t1-1）。

2.2 群密钥的产生

群密钥：由 KDC产生，即 d=[f（0）+g（0）]=a0+b0。

群公钥：Y=（a0+b0）·P。

Clerk随机地为用户pi选择群内公开身份ui∈Zq*。

2.3 群成员的加入

（1）群成员 pi随机选取 ki∈Zq*，并计算 Ri=ki·P=（xi，yi），并将（ki，Ki）在群内公开。

（2）签名服务者 Clerk通过验证 Ri≠Rj（i≠j）是否成立，来检验群成员pi、pj是否选择了同样的随机数。若Ri=Rj，说明这两个群成员选择了相同的随机数，则Clerk通知他们重新选取并进行计算。若Ri≠Rj，则进行下一步。

（4）Clerk验证 σi=H（ui||IDi）是否成立：

若 σi≠H（ui||IDi），则说明群成员 pi伪造了一个群内公开身份，Clerk拒绝pi加入签名生成过程，并通知KDC拒绝为其分发秘密钥碎片。

若 σi=H（ui||IDi），则接受 pi加入，通知 KDC为其分发秘密钥碎片。

（5）群成员的撤销。设该系统现有k（k≥t）个群成员，撤销群成员pj的过程如下：Clerk将pj在群内的公开身份uj置为1。在验证用户身份合法性时，若检测到σj=H（1），则拒绝 pj加入签名群，同时通知 KDC拒绝 pj为分发秘密钥碎片。

2.4 密钥分配及验证

（1）密钥分配

秘密钥碎片分 发采用 “双重”SSS[3]，分 别是（t，n）和（t1，n1）门限。将密钥d分割成多种组合，d的每种组合都与包含t个不同用户的子集相对应。

如果群成员pi是普通用户，则得到相对应的秘密碎片 di=f（xi），并由 KDC在群内广播其公钥 Yi=di·P=f（xi）·P；如果群成员pi是特权集用户，则得到的秘密碎片为di=[f（xi）+g（yij）]，由 KDC公开其公钥为 Yi=di·P=[f（xi）+g（yij）]·P。以上的过程利用“双重”SSS秘密共享方案为各群成员建立了公、私钥碎片。

最后，KDC 公开参数为：E（Fp），P，p，q，H（）。

（2）群成员对各自密钥的验证

根据 Pedersen VSS验证方法[5]，群成员 pi可通过式（1）和式（2）验证KDC为其分配的密钥di的有效性：若群成员pi为特权集用户，则验证：

若等式成立，证明KDC分配给群成员pi的密钥di是正确、有效的。否则就说明KDC欺诈。

2.5 单个签名生成与验证

假设现有t个群成员参与群签名的生成，设被签署的消息为m。则签名步骤如下：

项式得出。签名者pi发送（m，si）给 Clerk。

（3）Clerk验证单签名：Clerk接收到各个签名消息si后，利用签名者pi的公钥验证其单个签名的有效性，验证等式为:

若等式成立，则接受该单签名，否则拒绝接受单签名。

2.6 群签名的生成

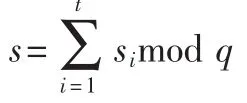
3 方案分析

3.1 正确性分析

（1）单签名的验证

假设至少有 t个人参与签名，且恰为 1，2，…，t，其中至少有t1个人属于特权用户集，并且签名者没有欺诈行为。不论是普通用户还是特权用户,都可以通过式（3）验证单签名的正确性。

上述过程验证了单签名的正确性。

（2）群签名的验证

假设签名组成员都严格按照签名的步骤对消息进行签名，就有

所以有：

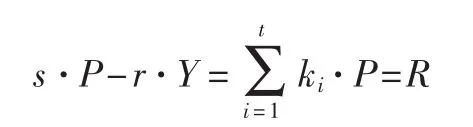
上述过程通过式（3）对群签名的正确性进行了验证。

3.2 安全性分析

根据门限群签名的特性对该方案进行安全性分析。

（1）匿名性

由于签名者使用的是公开身份，公开身份和真实身份的对应关系只有Clerk和签名者本身知道。其他用户只知道通过广播信道传播出的Ri的值，并不能依据Ri来确定用户的真实身份，也就无法根据群签名（在未经特许的情况下）追踪各签名方的真实身份。因此该方案具有匿名性。

（2）不可伪造性

参与签名的群成员只有获得合法身份，才能获得秘密钥碎片进而生成有效的部分签名，非法用户无法伪造有效部分签名。Clerk通过验证σi=H（ui||IDi）来确定群成员的身份是否合法。

（3）可追查性

如果事后签名出现矛盾，在得到许可的情况下，需要调查哪些成员参与签名，Clerk很容易确定签名方的真实身份。

（4）抗合谋攻击

在秘密钥碎片的分发上采用“双重”SSS。当进行合谋攻击时，如果不符合特权条件的要求，即使有t个或t个以上签名者参与，g（0）的恢复也是不可能的，进而无法得到群密钥；如果有不足t个人参与签名，即使符合特权条件的要求（g（0）可以恢复）也不可能恢复 f（0），从而无法得到群密钥。可见，该方案能抵抗合谋攻击。

（5）可撤销性

签名者pi被撤销后，在开始新的签名过程时，KDC公布了新的Y′，pj就不能继续参与群签名的生成，因为此时群公钥由原来的Y变成了Y′。

若签名者pj继续使用原来的私钥dj参与新的群签名的生成，Clerk在收到 pj的单签名 sj后，要根据 pj的公钥Yj验证式（3）是否成立。然而Clerk在信道内无法获得与 pj相对应的 Yj，也就无法验证式（3），因此 Clerk拒绝接受该单签名。所以，被撤销后的签名者pj并不能继续参与群签名的生成。

（6）门限特性

由于方案是基于双重Shamir秘密共享建立的，因此在签名阶段具有门限方案的安全性：任意少于t个群的成员无法得到有效签名，且任意少于t1个特权集成员也无法得到有效签名。

3.3 效率分析

本方案的建立基于椭圆曲线密码体制，与ElGamal类型的基于离散对数问题的原方案相比密钥长度和签名长度都大大降低。

ECC算法只需采用较短的密钥就可达到与离散对数算法相同的加密强度。ECC算法具有每比特最高的安全强度。由于智能卡在CPU处理能力和RAM大小上受限，采用一种运算量小但同时能提供高加密强度的公钥密码机制对于实现数字签名的应用非常关键。ECC在这方面具有明显的优势，160 bit ECC算法的安全性与1 024 bit采用基于离散对数问题的算法安全性相同。因此，采用椭圆曲线密码体制设计的门限群签名方案的计算量和通信量都要小于基于离散对数问题的ElGamal密码体制的门限群签名方案。

本文基于椭圆曲线密码体制和双重Shamir秘密共享体制，结合Chen Feng的特权集思想，设计了一个同时具有门限群签名功能和门限共享验证功能的存在特权集的门限群签名方案，该方案不但克服了目前一些方案的缺陷和弱点，而且具有更高的实现效率。方案除了具有门限群签名的性质外，还可以利用公开验证功能防止KDC欺诈。相对于原方案，本方案是基于椭圆曲线密码体制建立的，在安全性和效率方面考虑得更全面。但是，如何将该方案推广到实际应用中，仍有待于进一步研究。

[1]BELLARE M，MICCIANCIO D，WARINSCHI B.Foundation of group signatures:formal definitions,simplified requirements,and a construction based on generalassumptions[C].Proc of EUROCRPT 2003，LNCS2656.Berlin:Springer-Verlag，2003：614-629.

[2]王贵林，卿斯汉.几个门限群签名方案的弱点[J].软件学报，2000，11（10）：1326-1332.

[3]陈伟东，冯登国.一类存在特权集的门限群签名方案[J].软件学报，2005，16（7）：1289-1295.

[4]石怡，冯登国.一类新型（tj，t，n）-门限群签名方案的设计与分析[M].北京：科学出版社，2000.

[5]彭长根，李祥，罗文俊.一种面向群组通信的通用门限签密方案[J].电子学报，2007，35（1）：64-67.

Threshold group signature scheme with privilege subsets based on ECC

Dong Yurong

（Computer Science and Information College,Guizhou University,Guiyang 520025，China）

Through the analysis and study of a threshold group signature scheme which is based on ElGamal type,in order to solve the deficiency of the scheme,a new threshold group signature scheme with privileged subsets based on ECC is proposed.The proposed scheme can prevent the fraud of KDC efficiently.Only when the scheme satisfiesand（t，n）and（t1，n1）threshold signature,the valid signature can be generated,thus the scheme reached the property of threshold.The program also has the properties of threshold group signature.

privileged subjects；secret sharing；threshold group signature；ECC

TP309

A

1674-7720（2011）02-0089-04

2010-07-31）

董玉蓉，女，1985年生，硕士研究生，主要研究方向：密码学与信息安全。