沉底水雷爆炸威力的数值计算*

姚熊亮，杨文山，陈 娟，张阿漫，初文华

（哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001）

沉底水雷爆炸威力的数值计算*

姚熊亮，杨文山，陈 娟，张阿漫，初文华

（哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001）

采用冲击波物理中的阻抗匹配镜像线方法处理物质交界面，利用无网格光滑粒子流体动力学法（smoothed particle hydrodynamics，SPH）方法模拟沉底装药的水下爆炸过程，得到了不同方向不同爆距处的峰值压力反射系数，分析了爆炸流场参量分布和变化规律，研究了不同水底砂层厚度和不同装药量对爆炸冲击波传播和流场中压力的影响。结果表明：海底反射系数随测点与水平线夹角的变化而变化，当测点与水平线夹角为约55°时反射系数最大，其最大值可达1.5。本文的研究可为沉底水雷爆炸载荷的确定提供参考。

爆炸力学；反射系数；SPH方法；沉底水雷；水下爆炸；阻抗匹配

炸药沉底爆炸是一个涉及边界效应的复杂爆炸动力学问题，爆炸冲击波由海水介质入射到海底界面，在界面以下底质中的冲击阻抗与海水中冲击阻抗不同，从而产生反射和透射冲击波或稀疏波，即在水底附近形成复杂的相互作用波系，目前这方面的理论研究还很不成熟［1］。对于沉底水雷等装药沉底爆炸，B.V.Zamyshlyayev［2］认为水底附近反射波与入射波相互作用非常复杂，不能用水底反射理论进行分析，一般把它简化为无限场来处理，等效为1.70倍药量在无限场爆炸，这样处理对不靠近水底的测点在压力峰值上有一定精度，但对水底附近的测点精度很低。金辉等［3］利用Autodyn软件对装药沉底爆炸进行了模拟研究，得到了水底反射对药包上方范围起到增强作用，而对水底附近起削弱作用的相关结论，但并未对不同区域处的水底反射系数做进一步的分析。顾文彬等［4－6］利用有限元ALE算法模拟了沉底装药爆炸问题。已有的对沉底装药爆炸问题的研究均是采用基于网格的数值算法，在涉及高密度比的间断面求解时，需要进行特殊处理，界面计算过程较复杂。无网格方法可以弥补基于网格的数值方法的一些缺陷，不受网格划分的限制，可以解决在基于网格的数值方法中由于高压、高能、大变形等导致网格畸变而计算崩溃的问题。为此，本文中采用阻抗匹配镜像线方法来处理水－砂界面，研究冲击波与海底的相互作用机理，利用SPH方法模拟沉底装药的水下爆炸过程，以期对认识沉底爆炸流场参量分布和变化规律有一定的帮助。

1 SPH计算方法

水中炸药的起爆速度和冲击波的传播速度很快，可以假设爆炸气体和水都是无粘性的且绝热的。将药包放置在海底砂层附近的沉底接触爆炸过程中，砂层直接承受强烈的冲击波作用，此时可认为砂层几乎丧失传递剪切力的能力，呈现出流体的性质，因此可近似地将海底砂质土壤处理成流体。本文中使用Euler方程和状态方程来模拟整个沉底水下爆炸过程

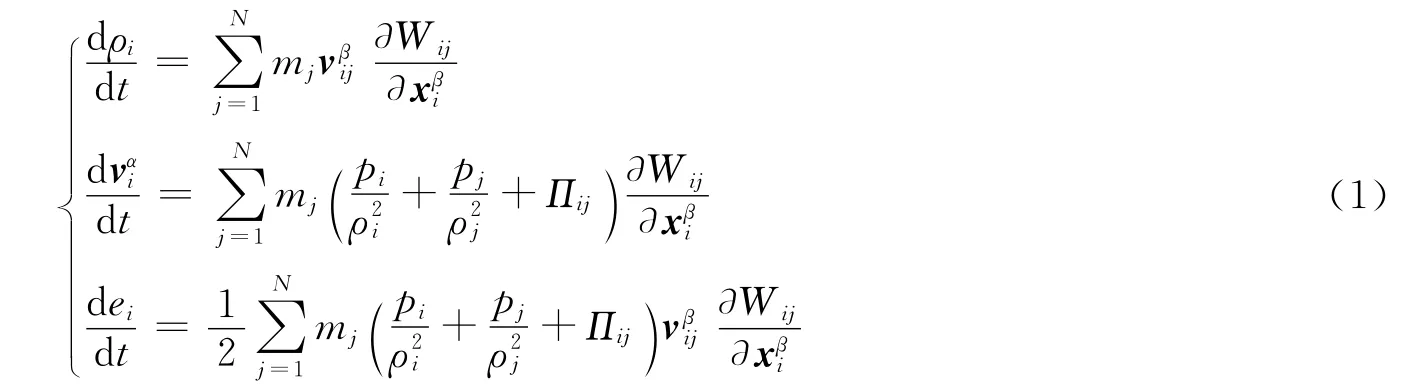
式中：m、ρ、v、p、e分别为粒子的质量、密度、速度、压力和内能；i、j代表相互作用的2粒子；α、β表示坐标方向；Πij为Monaghan型［7］人工粘性，可防止求解结果的非物理振荡和粒子间的非物理穿透；Wij为光滑函数，本文中采用分段五次样条光滑核函数近似水下爆炸控制方程。

本文中，对爆炸气体采用JWL状态方程［8］；对水采用 Mie-Grüneisen状态方程［9］；对水底砂层采用多项式状态方程［10］，它是流体物态方程的经验形式，在压缩和膨胀状态下的压力分别为

式中：a1、a2、a3、b0、b1、b2为物态方程经验系数；μ 为压缩比，e为内能。

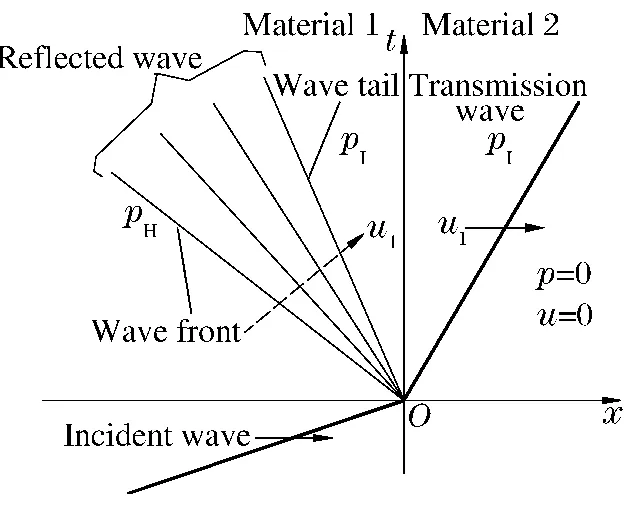
图1 冲击波的透射与反射Fig.1Transmission and reflection of shock wave

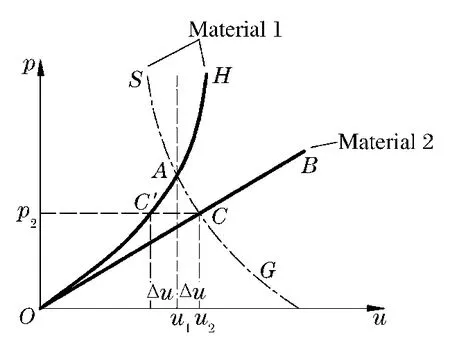
图2 镜像线近似原理Fig.2 Approximation principle of mirror image

2 阻抗匹配镜像线方法

水下爆炸过程中，当冲击波通过2种物质的界面时，会因为2种物质的冲击阻抗不同而发生反射和透射，从而产生反射冲击波和反射稀疏波。在SPH方法中，物质交界面处理非常重要，也是一个难点。SPH方法具有拉格朗日性质和粒子性质，在整个演变过程中，来自不同介质的相互接触的粒子可能会随着运动而分离，甚至可能不再成为相邻粒子。目前，大多数利用SPH方法处理水下爆炸的气－水界面时都采用粒子对粒子的界面算法［9］，能达到很好的效果，也能有效地防止粒子间的非物理穿透。然而将此方法运用到水砂界面的处理时却遇到了困难，不能简单地将气、水粒子间的惩罚力直接施加在水砂粒子上，而关于惩罚力的形式和其中参数的取值目前还未见报道。由于水下爆炸流场压力都处于20GPa以下，假设整个水下爆炸过程是等熵绝热过程，所以本文中采用冲击波物理中的阻抗匹配镜像线方法［11］来处理水－砂界面，根据界面两侧材料的力学平衡原理和界面连续性条件，由水的冲击绝热线计算砂土的冲击绝热线。

在阻抗匹配镜像线法中，利用介质1的冲击绝热线的镜像对称线来近似地作为等熵卸载线，进而来获得介质2的阻抗匹配解，如图1～2所示。

假设ρ01c01＞ρ02c02，界面处产生反射稀疏波。对于C′点，其粒子速度为u1－Δu，由于C点的压力与C′点的压力相等，即pC＝pC′，其中pC′＝ρ01［c01＋λ1（u1－Δu）］（u1－Δu），pC＝p2＝ρ02D2（u1＋Δu），则有

式中：ρ01和ρ02分别为介质1和2的初始密度，c01、λ1、c02、λ2为介质1和2的冲击绝热系数，D2为介质2中的冲击波速度。整理式（3）得到关于Δu的二次方程

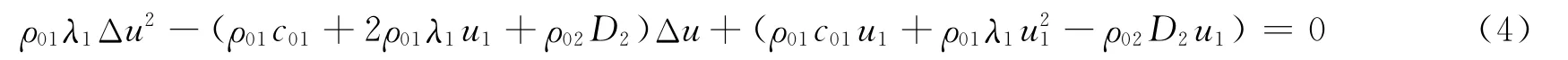
解此方程得

式中：a＝ρ01λ1，b＝－（ρ01c01＋2ρ01λ1u1＋ρ02D2），c＝ρ01c01u1＋ρ01λ1u21－ρ02D2u1。则介质2在C状态下的粒子速度和压力分别为

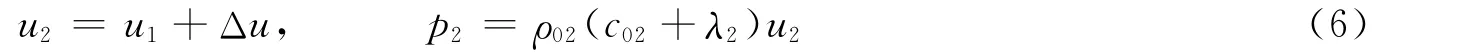
同理，当ρ01c01＜ρ02c02时，可得到与式（6）相同的阻抗匹配解。

以一维问题为例，说明阻抗匹配镜像线法在SPH粒子系统中的实施过程，如图3所示。入射波传播过程中，当界面处的粒子1满足

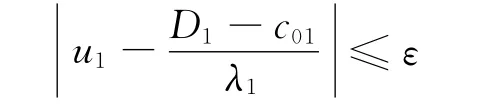
时，就认为入射波到达界面处，式中ε为控制系数，D1为物质1中的冲击波速度。通过以上阻抗匹配解计算公式，可得到入射波通过界面时粒子2的运动速度u2和压力p2，此时粒子2的状态量变为ρ02、u2、p2。然后冲击波以ρ02、u2、p2为初始条件继续在介质2的粒子中传播。这样，入射冲击波便完成了界面处的反射和透射。

图3 2种物质间的运动界面Fig.3 Moving interface between two materials

3 数值计算结果分析

3.1 计算模型

为使问题简化，假设：（1）水介质为海水；（2）海底砂层均匀平整，由各组分通过理想混合法则组成；（3）砂层下的基岩为固壁。海水计算尺寸为5m×2.5m；TNT方形装药质量为36kg，炸药尺寸为0.15m×0.15m，中心坐标为（0m，0m）；海底砂层计算尺寸为5m×0.5m。整个计算区域离散成24 000个粒子。几何构形如图4所示，其中r为等效药包半径，R为测点距药包中心的距离。

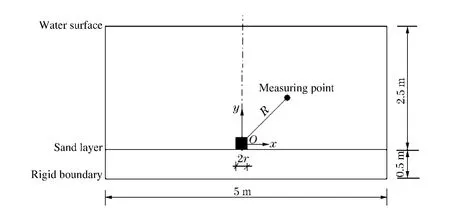
图4 计算模型的几何构形Fig.4 Geometrical model of example

3.2 水中冲击波的传播

图5为炸药沉底爆炸的压力分布云图。从图中可清晰地观察到，炸药起爆后冲击波同时向水中和砂层中传播，由于砂土粒子的冲击阻抗大于水粒子的冲击阻抗，所以砂层区域的压力高于水中的压力，如图5（a）所示。随着冲击波的不断向前传播，在约0.4ms时冲击波已到达砂层以下的固壁，并向砂层中反射冲击波，使砂层中的压力又逐渐增高，如图5（b）所示。由固壁反射回的反射波传入水中，所以此后水域流场的压力变化是一系列爆炸冲击波和反射冲击波共同作用的结果。

图5 不同时刻的压力分布Fig.5 Pressure distribution at different times

水底砂层土壤和砂底固壁反射的冲击波和爆炸冲击波的相互作用使水中冲击波的峰值压力和衰减规律与无限水域中有较大的差别，尤其是水底附近区域，如图6所示。图中所示为36kg的TNT炸药沉底爆炸水域中爆距分别为0.45、0.60、0.75、0.90m，与水平线夹角分别为0°、45°、90°的点的压力时历曲线。在0°方向上的压力曲线出现了2个峰值，分别是入射的爆炸冲击波作用和从砂底固壁反射的冲击波所致，随着冲击波的传播，在0.75和0.90m处反射冲击波的峰值压力甚至超过了直达波；在45°和90°方向上受到反射冲击波作用微弱得多。

图6 不同爆距不同方向上的压力曲线Fig.6 Pressure curves in different directions at different distances from the explosion center

3.3 爆炸流场压力分布和变化规律

为了研究炸药沉底爆炸时水底对流场压力分布的影响和变化规律，提取了在不同爆距处与水平方向每隔10°的考察点的峰值压力，即与水平方向成θ处的第1次压力峰值，即pθ，并与自由场中经验公式的计算峰值pCole进行比较，如图7所示。由图中可以看出在沉底爆炸时存在明显的水底反射现象，且θ在0°～20°范围内压力削弱，30°～90°范围内压力增强，当θ＞50°时冲击波压力峰值增加到一个相对稳定的值，这一结论与文献［3］一致。

图7 不同方向不同爆距处的峰值压力比较Fig.7 Comparisons of peak pressures in different directions at different distances from the explosion center

为了进一步研究砂质水底的压力反射系数，定义峰值压力反射系数

由于θ＝0°～10°的流场区域内受砂底固壁影响较严重，双峰现象较明显，在数值计算的时间范围内，只考虑水底砂层反射波的作用，即pθ为第1次压力峰值。图8给出了不同方向不同爆距处的压力峰值反射系数γθ的分布情况。由图中可知，在水底0°附近区域内各测点的压力峰值比自由场中爆炸的压力峰值小。这是由于砂质土壤在高压爆炸产物的作用下，迅速变形成坑，消耗了一部分爆炸能量，引起水底附近冲击波压力的削弱。随着冲击波在砂层中的传播，砂层不断被压实，会在水－砂界面处反射压缩波；当到达砂底的固壁时也会反射回冲击波作用于水域流场中，所以水底附近区域水介质受到不同性质的波系的影响，相互作用也较复杂。随着θ的不断增大，γθ也不断增大，且呈现出一定的规律。在50°～60°附近，γθ达到最大，并随θ的继续增大，水底砂层和砂底固壁的反射作用逐渐减弱，所以γθ也随之减小。此外，在一定角度θ上，γθ也随着爆距的增大呈现增大的趋势，在R／r＝26时，即爆炸的中远场处，各个角度θ上的γθ值基本处于1.4～1.6之间，与目前工程计算中所取的压力峰值反射系数基本一致。

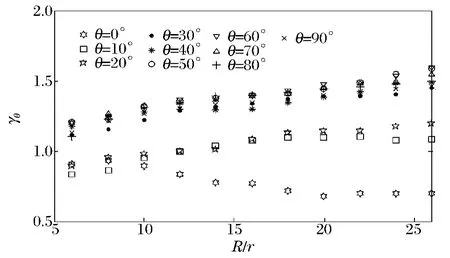
图8 不同方向不同爆距处的反射系数Fig.8 Reflection coefficient in different directions at different distances from the explosion center

3.4 不同砂层厚度对计算结果的影响

为了研究沉底装药爆炸时砂层厚度对水域流场压力的影响，选取了36kg炸药在不同厚度的砂层上爆炸的计算模型，得到0.45m处0°、45°、90°方向上的压力曲线（见图9），其中δ为砂层厚度。从图中可以看出，砂层厚度对水域介质压力的变化的影响较大，尤其是砂层较薄（δ＝0.1，0.2m）时砂层吸收爆炸能量较少，反射冲击波的能力也较弱，此时砂底固壁的反射作用是压力曲线出现双峰的主要原因，并对第2个压力峰值作主要贡献。随着δ增加到1.0m后，在1.2ms内，再增加砂层厚度对此处的压力变化几乎没有影响，压力曲线几乎完全重合。

图9 不同砂层厚度不同方向在0.45m处的压力曲线Fig.9 Pressure curves at at 0.45min the case of different sand thickness and directions

3.5 不同装药质量对计算结果的影响

本文中还研究了不同装药质量对沉底爆炸冲击波压力变化规律的影响。表1中给出了冲击因子C2＝／R 时0°、45°、90°方向上的峰值压力。由表1能明显地看出各个方向上压力峰值相差较大，且随着药量的增加而增大，此时自由场中药量和爆距之间的相似定律在沉底爆炸时已不再成立，必须探索新的相似规律。

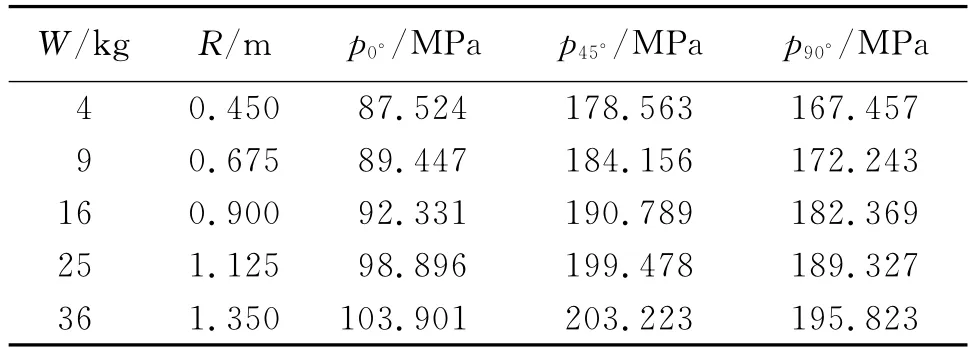
表1 不同装药量的峰值压力比较Table 1 Comparisons of peak pressures for different TNT mass

4 结 论

利用无网格SPH算法对存在砂质土壤的海底沉底爆炸问题进行了数值模拟，水下爆炸时冲击波与不同物质界面的相互作用而产生的反射和透射现象在计算中基本得到了正确的再现。得到了沉底爆炸时不同方向的峰值压力反射系数γθ及其变化规律，在0°～5°范围附近γθ＜1.0；在50°～60°附近γθ达到最大，并随着θ的增大，γθ随之减小；在中远场处，各个角度θ上的γθ基本处于1.4～1.6之间。此外不同砂层厚度和装药量对计算结果的影响也较大，尤其是不同装药量时需要进一步探索新的相似规律。

［1］蒋国岩，金辉，李兵，等.水下爆炸研究现状及发展方向展望［J］.科技导报，2009，27（9）：87-91.

JIANG Guo-yan，JIN Hui，LI Bing，et al.Review of studies on underwater explosion［J］.Science ＆ Technology Review，2009，27（9）：87-91.

［2］Zamyshlyayev B V.Dynamic loading in underwater explosion［R］.AD-757183，1973.

［3］金辉，张庆明，高春生，等.装药水下沉底爆炸压力场特性研究［J］.科技导报，2009，27（14）：32-37.

JIN Hui，ZHANG Qing-ming，GAO Chun-sheng，et al.Characteristics of pressure field in ground explosion［J］.Science ＆ Technology Review，2009，27（14）：32-37.

［4］顾文彬，马海洋，唐勇，等.水底对浅水中装药爆炸效果的影响［J］.爆破，2003，20（4）：88-92.

GU Wen-bin，MA Hai-yang，TANG Yong，et al.Influence of water bottom on the explosion effect of shallow-layer water charging［J］.Blasting，2003，20（4）：88-92.

［5］顾文彬，叶序双，张朋祥，等.浅层水中爆炸水底影响的试验研究［J］.解放军理工大学学报，2001，2（2）：55-58.

GU Wen-bin，YE Xu-shuang，ZHANG Peng-xiang，et al.Experimental studies of bottom influence in shallow-layer water explosion［J］.Journal of PLA University of Science and Technology，2001，2（2）：55-58.

［6］顾文彬，阳天海，叶序双，等.单个装药浅层水中沉底爆炸的数值模拟［J］.解放军理工大学学报，2000，1（3）：41-45.

GU Wen-bin，YANG Tian-hai，YE Xu-shuang，et al.Numerical simulation of single charge explosion on seabed in shallow water［J］.Journal of PLA University of Science and Technology，2000，1（3）：41-45.

［7］Monaghan J J，Lattanzio J C.A refined particle method for astrophysical problems［J］.Astronomy and Astrophysics，1985，149（1）：135-143.

［8］Liu M B，Liu G R，Zong Z，et al.Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology［J］.Computers and Fluids，2003，32（3）：305-322

［9］Liu M B，Liu G R，Lam K Y.Investigations into water mitigations using a meshless particle method［J］.Shock Waves，2002，12（3）：181-195

［10］王继海.多项式形式物态方程及其等熵线［J］.爆炸与冲击，1992，12（1）：1-10

WANG Ji-hai.Polynomial form of Mie-Grüneisen equation of state and its isentropic［J］.Explosion and Shock Waves，1992，12（1）：1-10.

［11］谭华.实验冲击波物理导引［M］.北京：国防工业出版社，2005：1-121

Numerical calculation of explosion power of mines lying on seabed＊

YAO Xiong-liang，YANG Wen-shan，CHEN Juan，ZHANG A-man，CHU Wen-hua
（College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，Heilongjiang，China）

The underwater explosion process of mines lying on seabed was simulated by using the meshfree SPH method.And the substance interfaces were treated by adopting the impedance matching method.The reflection coefficients of the peak pressures in different directions at different distances from the explosion center were obtained.The distribution and change of the explosion field parameters were analyzed.And the effects of different sand thickness and different charge mass on shock wave propagation and pressure were discussed.Simulation results show that the seabed reflection coefficient varies with the angle between measuring points and horizontal line and it arrives at the maximum value of 1.5when the angle is about 55degree.It is helpful for determining the explosion load of mines lying on seabed.

mechanics of explosion；reflection coefficient；SPH method；mines lying on seabed；underwater explosion；impedance matching

21August 2009；Revised 4October 2010

YANG Wen-shan，wenshanyang85＠gmail.com

（责任编辑 张凌云）

O382.4；U661 国标学科代码：130·3520

A

1001-1455（2011）02-0173-06＊

2009-08-21；

2010-10-04

国家自然科学基金项目（50939002，10976008，50809018）

姚熊亮（1963— ），男，教授，博士生导师。

Supported by the National Natural Science Foundation of China（50939002，10976008，50809018）