含坑点腐蚀的深海耐压球壳有限元分析

徐 强，万正权

（中国船舶科学研究中心，江苏 无锡 214082）

含坑点腐蚀的深海耐压球壳有限元分析

徐 强，万正权

（中国船舶科学研究中心，江苏 无锡 214082）

对于含坑点腐蚀等局部缺陷的球壳结构，由于结构的不连续性以及缺陷部位应力状态的三维特性，因此很难用传统的连续介质理论及板壳理论进行求解。为了对含坑点腐蚀的球壳的强度、稳定性进行精确分析，文中分别采用坑点腐蚀壳体单元（Pitting Corrosive Shell Element,PCSE）、基于多点约束（Multipoint Constraint,MPC）的壳体单元—实体单元集成以及实体单元三种方法进行对比计算，对比结果表明，采用PCSE方法的计算效率最高，且计算结果的精度满足工程应用要求。最后，基于PCSE方法并通过方差分析，讨论了坑点腐蚀对球壳强度及稳定性的影响。

坑点腐蚀；强度；稳定性；多点约束；方差分析

1 引 言

球壳作为一种理想的耐压结构形式在海洋结构物中得到大量应用，由于海水的腐蚀作用，导致老龄球壳结构通常存在严重的腐蚀问题，坑点腐蚀是常见且危害极大的一种，坑点腐蚀属于非均匀腐蚀，是由于金属表面物理和化学的不均匀性所引起的。严重的坑点腐蚀可能使金属壳板穿透，引起严重的安全事故，因此，开展本文的研究工作是极其必要的。

对于船舶及海洋结构物的坑点腐蚀问题，国内外学者及相关机构已做了大量的研究，TSCF[1]、Daidora[2]等开展了坑点腐蚀钢板的等效厚度及剩余厚度研究，Flaks[3]、Paik[4-6]开展了坑点腐蚀对板构件及老龄船舶的极限强度的影响研究，Dunbar[7]、Nakai[8-9]等开展了坑点腐蚀对船舶典型构件的局部强度的影响研究，王燕舞[10-11]等开展了船舶结构钢海洋环境最大坑点腐蚀深度及蚀坑形态与径深比的时变模型研究，徐强、万正权[12-13]开展了坑点腐蚀板的等效材料常数研究及含坑点腐蚀的壳体有限元方法研究。

对于含坑点腐蚀等局部缺陷的球壳结构，由于结构的不连续性以及缺陷部位应力状态的三维特性，因此很难用传统的连续介质理论及板壳理论进行求解。本文分别采用坑点腐蚀壳体单元PCSE[13]方法、基于多点约束MPC的shell-solid集成方法以及实体单元方法对含坑点腐蚀的耐压球壳的强度和稳定性进行计算分析，并对比了三种有限元方法的计算效率和计算结果的精度，最后基于PCSE方法并通过方差分析，讨论了坑点腐蚀对球壳强度及稳定性的影响。

2 计算方法

本节主要对三种计算方法所采用的单元以及在计算中进行的一些处理进行简要介绍。

坑点腐蚀壳体单元PCSE[13]（Pitting Corrosive Shell Element）采用分层力学模型，并基于超参数壳体单元推导PCSE的单元刚度矩阵和单元节点载荷向量。PCSE的分层模型如图1所示，单元分为腐蚀层和完好层，腐蚀层的材料常数取等效的弹性模量和等效的泊松比[12]。单元的刚度矩阵通过沿壳体厚度方向的分段积分求得，在推导单元节点载荷向量时考虑了由腐蚀引起的偏心载荷，在求解单元应力时考虑了坑点腐蚀应力集中的影响，并对单元应力进行了修正。

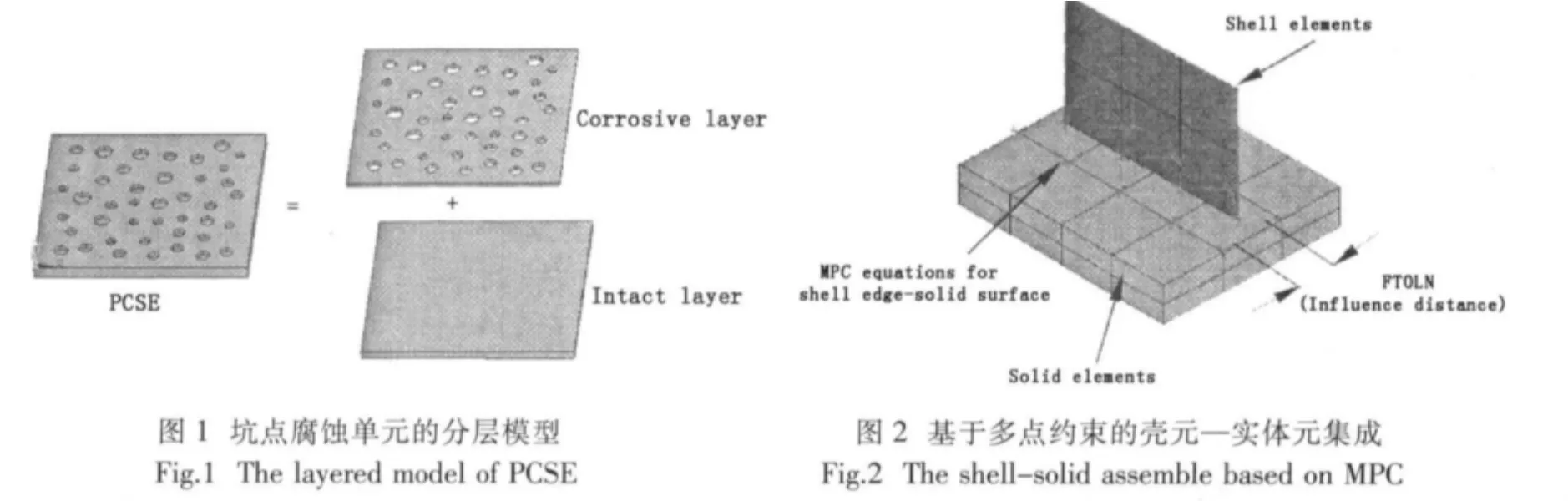
PCSE的腐蚀参数包括腐蚀强度DOP（Degree of pitting corrosion intensity）、蚀坑半径和蚀坑深度，其中腐蚀强度DOP等于腐蚀面积与单元面积的比值，即

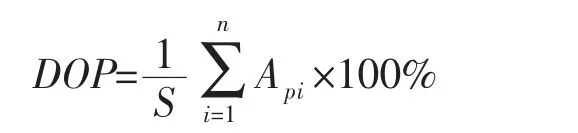
式中，Api是第i个蚀坑的面积，n为蚀坑个数，S为单元面积。

基于多点约束的壳元—实体元集成方法主要用于解决工程实际中遇到的三维连续实体结构和薄壁板壳结构的连接问题。由于壳体单元与实体单元节点形式与自由度不一致，为了保证交界面上的位移协调，根据板壳理论的基本假定：壳体中面的法线变形后仍保持为直线，因此要求变形后壳体单元与实体单元交界面上各点位移沿垂直于该面方向的分量相同，即两类单元在该交界面上仍保持贴合。基于上述讨论，建立起交界面上各节点自由度之间的约束方程，即为多点约束方程。图2为基于多点约束的壳元—实体元集成的示意图。

实体单元主要用于三维连续实体结构的建模，实体单元包括8节点六面体单元、高阶的20节点六面体单元以及退化的四面体单元，每个单元节点有三个自由度：x、y、z方向的平动自由度。六面体单元相比四面体单元具有更高的计算精度。

3 计算模型

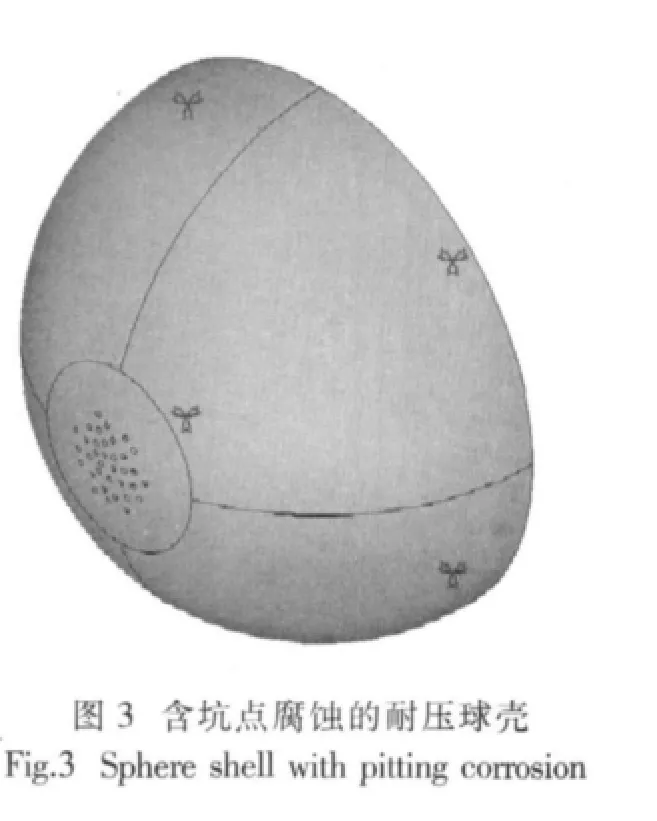
含坑点腐蚀的耐压球壳几何模型如图3所示，模型为半球，坑点腐蚀分布在球冠顶部，蚀坑呈圆柱形。模型几何参数如下：球壳外径Ro=500mm，球壳内径Ri=480mm，腐蚀强度DOP=12%，蚀坑深度h=15mm，蚀坑半径r=5mm。

有限元模型分别如图4～6所示，图4采用PCSE划分网格，单元总数为5 223，节点总数为5 286；图5的坑点腐蚀部位采用8节点六面体单元划分网格，其它部位采用4节点壳元划分网格，在壳元与实体元的交界面上进行多点约束，单元总数为34 678，节点总数为42 162；图6采用8节点六面体单元划分网格，单元总数为63 244，节点总数为64 686。模型采用固支边界，如图3所示。

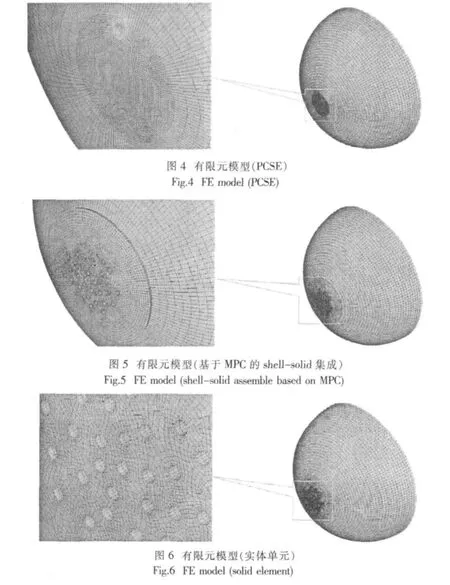
4 计算结果及分析

4.1 强度计算

在进行强度计算时，计算压力取25MPa，压力被施加在球壳外表面，材料弹性模量取1.96E5MPa，泊松比取0.3，材料屈服强度为785MPa。经过有限元数值计算，模型的合成位移云图及von Mises等效应力云图如图7～12所示，由图可知，模型的最大合成位移和最大von Mises等效应力均出现在坑点腐蚀部位。

4.2 稳定性计算

经过线弹性屈曲计算，模型的屈曲变形如图13～18所示。

4.3 对比分析

表1为三种计算方法关于CPU计算时间、强度计算结果以及稳定性计算结果的对比情况。

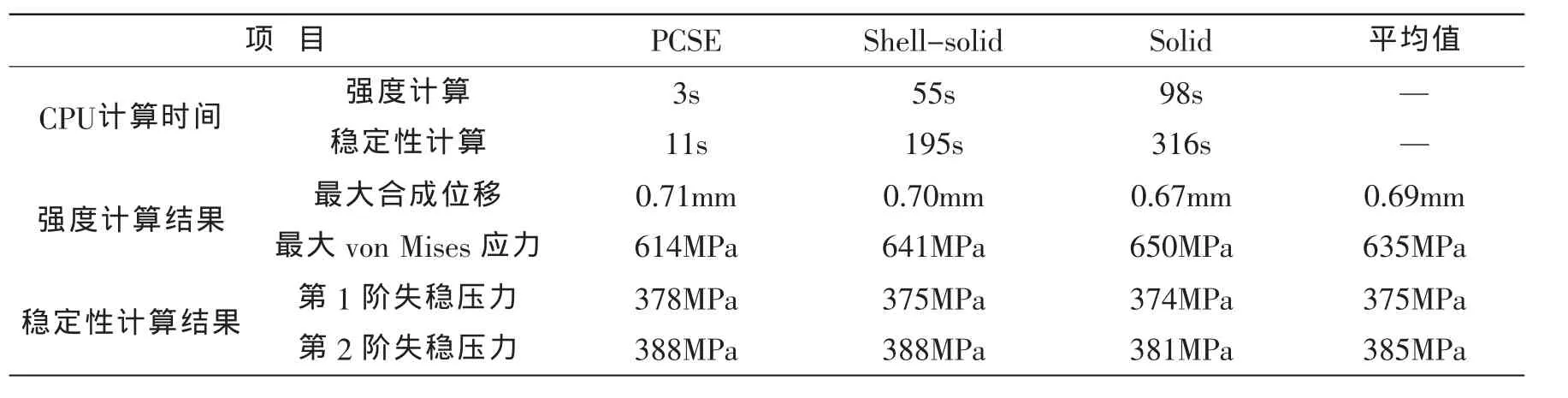
表1 计算效率及计算结果对比Tab.1 The comparison of computation efficiency and results

对比CPU计算时间发现，采用PCSE方法的计算时间最短，即计算效率最高，在进行强度计算时计算效率分别是基于MPC的shell-solid方法和solid方法的18.3倍和32.7倍；在进行稳定性计算时计算效率分别是基于MPC的shell-solid方法和solid方法的17.7倍和28.7倍。

对比强度计算结果发现，PCSE、基于MPC的shell-solid集成及solid方法的最大合成位移相对平均值的误差分别为2.8%、1.4%和-2.8%，最大von Mises应力相对平均值的误差分别为-3.3%、0.9%和2.3%，这表明三种方法的强度计算结果的精度满足工程应用要求。

对比稳定性计算结果发现，PCSE、基于MPC的shell-solid集成及solid方法的一阶失稳压力相对平均值的误差分别为0.8%、0.1%和-0.2%，二阶失稳压力相对平均值的误差分别为0.8%、0.8%和-1.0%，这表明三种方法的稳定性计算结果的精度满足工程应用要求。

5 坑点腐蚀对球壳强度及稳定性的影响分析

根据第四节的分析可知，在对含坑点腐蚀的球壳进行强度和稳定性分析时PCSE方法是高效且可靠的，本节将采用PCSE方法定量探讨坑点腐蚀对球壳强度及稳定性的影响。

首先确定三个无量纲腐蚀参数：DOP、h/t、r/h，其中DOP是腐蚀强度，h/t是坑点腐蚀深度与球壳厚度的比值，r/h是坑点腐蚀的半径与深度的比值。然后采用方差分析讨论腐蚀参数DOP、h/t、r/h对球壳强度和稳定性的显著性影响程度，方差分析首先假设腐蚀参数不影响球壳的强度和稳定性，然后构造小概率事件并进行计算，若计算结果表明小概率事件发生了，则拒绝该假设并认为该参数有显著影响；反之，则接受假设并认为该参数没有显著影响。

本文采用基于L9（34）的正交表方案进行计算，球壳的半径、厚度同第三节，每个腐蚀参数取三种水平，DOP：5%、10%、15%，h/t：1/4、2/4、3/4，r/h：1/1、1/2、1/3。 经过一系列计算，计算结果如表 2 所示。

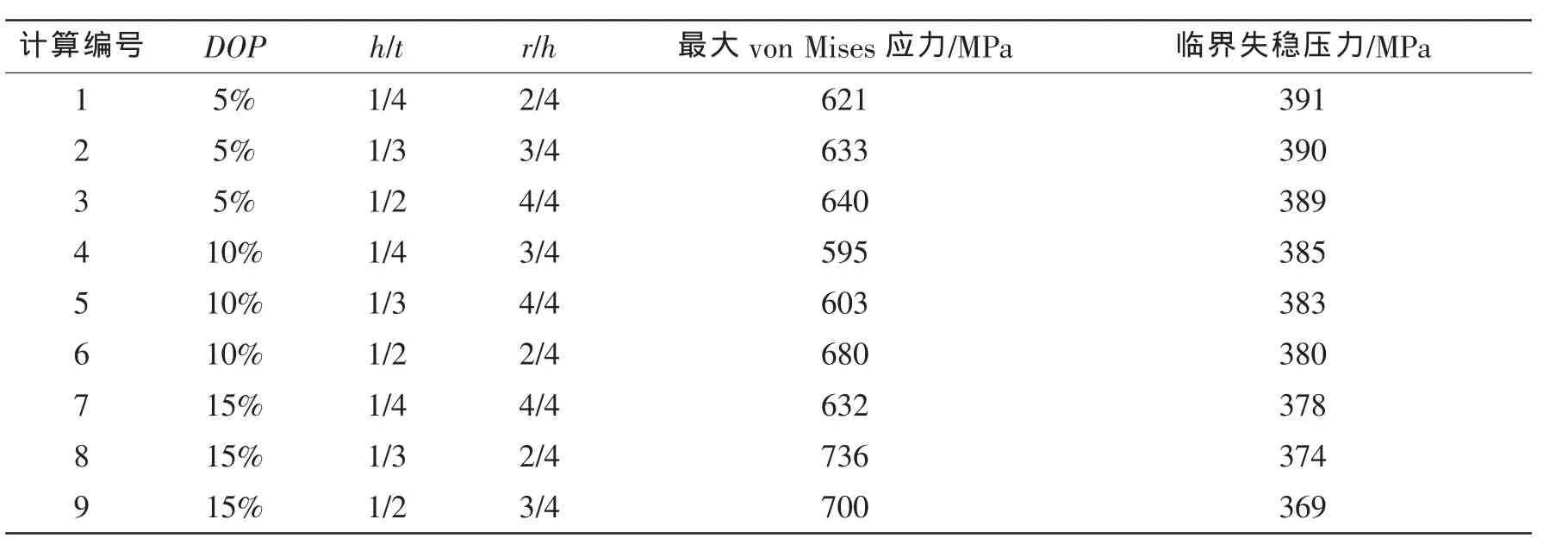
表2 含坑点腐蚀的球壳强度及稳定性计算结果Tab.2 The strength and buckling results of sphere shell with pitting corrosion

为了便于表达，用A、B、C分别表示DOP、h/t、r/h，用Ⅰ、Ⅱ、Ⅲ分别对应每个参数的三种水平。首先讨论腐蚀参数对最大von Mises等效应力σeq的显著性影响，记

QA，QB，QC分别为参数 A、B、C 引起的离差平方和，QE为误差。

根据数理统计理论，FA=QA/QE，FB=QB/QE，FC=QC/QE，分别服从自由度为（2，2）的 F 分布，给定显著性水平 α=5%，查数学用表可得Fα（2,2）=19。

根据表1可得FA=20.03，FB=14.21，FC=12.31，显然FA＞F0.05（2,2 ），拒绝假设，表明DOP对 σeq有显著影响；FB＜F0.05（2,2），FC＜F0.05（2,2 ），接受假设，表明h/t、r/h对 σeq没有显著影响。

同理，腐蚀参数对临界失稳压力Pcr的显著性影响分析结果如下：根据表1可得FA=72.28，FB=7.72，FC=1.24，显然FA＞F0.05（2,2），拒绝假设，表明DOP对Pcr有显著影响；FB＜F0.05（2,2），FC＜F0.05（2,2 ），接受假设，表明h/t、r/h对Pcr没有显著影响。

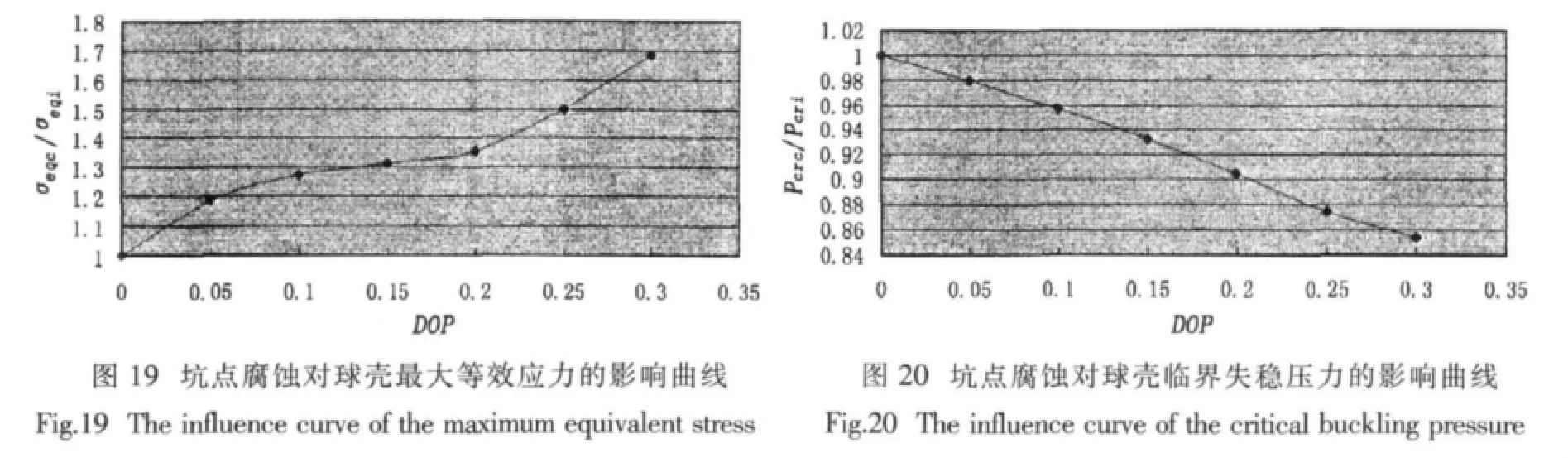
方差分析结果表明，腐蚀强度DOP对耐压球壳的强度和稳定性有显著影响，针对不同的DOP进行系列计算，其中0≤DOP≤0.3[14]，得到坑点腐蚀对耐压球壳的最大von Mises等效应力和临界失稳压力的影响曲线，如图19、20所示，图中σeqc、Pcrc分别表示含坑点腐蚀球壳的最大等效应力和临界失稳压力，σeqi、Pcri分别表示完好球壳的最大等效应力和临界失稳压力。由曲线可知σeqc/σeqi＞1，且随着腐蚀强度DOP的增加而单调递增，Pcrc/Pcri＜1，且随着腐蚀强度DOP的增加而单调递减，表明坑点腐蚀降低了耐压球壳的强度及稳定性，并随着腐蚀强度的增加其对球壳强度及稳定性的影响越大。

5 结 语

本文分别采用PCSE、基于MPC的shell-solid集成以及solid三种有限元方法对含坑点腐蚀的深海耐压球壳的强度和稳定性进行了对比计算，对比结果表明，采用PCSE方法的计算效率最高，计算效率分别是后两者的20倍至30倍，且计算结果相对平均值的误差小于5%，满足工程应用的要求。然后基于PCSE方法并通过方差分析，讨论了坑点腐蚀因素对球壳强度及稳定性的影响，方差分析结果表明，坑点腐蚀降低了球壳的强度及稳定性，且随着腐蚀强度DOP的增加其对球壳强度及稳定性的影响越大。

[1]TSCF.Experimental and theoretical investigation of the strength of corroded hull elements[R].Project 300,Report No.84-3438,Tanker Structure Co-operative Forum,1984.

[2]Daidora J C,Parente J,Orisamolu I R,Ma K T.Residual strength assessment of pitted plate panels[R].SSC-394,Ship Structure Committee,1997.

[3]Flaks V Y.Correlation of pitting corrosion of aluminum plates and reduction of load-beating capacity under tension[J].Fiziko-Khimicheskaya Mekhanika Materialov,1987,14(1):89-93.

[4]Paik J K.Ultimate strength of ships time-variant risk assessment of aging ship staking account to general/pit corrosion,fatigue cracking and local dent damage[R].Technical Report RD 2002-11,American Bureau of Shipping,2002.

[5]Paik J K,Wang G,Thayamballi A K,Lee J M.Time-dependent risk assessment of aging ships accounting for general/pit corrosion,fatigue cracking and local denting[C].SNAME Trans,2003,111.

[6]Paik J K,Lee J M,Ko M J.Ultimate shear strength of plate elements with pit corrosion wastage[J].Thin-Walled Structures,2004,42:1161-1176.

[7]Dunbar T E,Pegg N,Taheri F,Jiang L.A computational investigation of the effects of localized corrosion on plates and stiffened panels[J].Marine Structures,2004,17:385-402.

[8]Nakai T,Matsushita H,Yamamoto N,Arai H.Effect of pitting corrosion on local strength of hold frames of bulk carriers(1st report)[J].Marine Structure,2004,17:403-432.

[9]Nakai T,Matsushita H,Yamamoto N,Arai H.Effect of pitting corrosion on local strength of hold frames of bulk carriers(2nd report)-lateral distortional buckling and local face buckling[J].Marine Structure,2004,17:612-641.

[10]王燕舞,黄小平,崔维成.船舶结构钢海洋环境点蚀模型研究之一:最大点蚀深度时变模型[J].船舶力学,2007,11(4):577-586.

[11]王燕舞,吴晓源,张雨华,黄小平,崔维成.船舶结构钢海洋环境点蚀模型研究之二:实船蚀坑形态与径深比时变模型[J].船舶力学,2007,11(5):735-743.

[12]徐 强,万正权.坑点腐蚀板的等效材料常数研究[J].钢结构论文集,2008,23(115):15-20.

[13]徐 强,万正权.含坑点腐蚀的壳体有限元方法[J].船舶力学,2010,14(1-2):84-93.

[14]徐 强.考虑坑点腐蚀影响的耐压船体结构计算方法研究[D].无锡:中国船舶科学研究中心,2008.

[15]王勖成.有限单元法[M].北京:清华大学出版社,2003:406-413.

FE analysis of deep-sea sphere shell with Pitting corrosion under pressure

XU Qiang,WAN Zheng-quan
(China Ship Scientific Research Center,Wuxi 214082,China)

It is hard to analyse sphere shell with pitting corrosion by traditional continuous medium theory and shell mechanics theory because of structure discontinuous and 3D stress status.The strength and buckling analysis of sphere shell with pitting corrosion were carried out by Pitting Corrosive Shell Element,shell-solid assemble based on Multipoint Constraint and solid element respectively,and the computation efficiency and precision were also compared among the three FE analysis methods.The results show that PCSE is the most efficient and the results precision can meet the needs of engineering application.Finally,the influences of pitting corrosion on the strength and buckling of sphere shell was discussed via PCSE and variance analysis.

pitting corrosion;strength;buckling;multipoint constraint;variance analysis

U661.4

A

1007-7294（2011）05-0498-08

2010-12-14

徐 强（1981-），男，硕士，中国船舶科学研究中心工程师；

万正权（1962-），男，中国船舶科学研究中心研究员，博士生导师。