应用教学与思维训练相结合的高职高专高等数学教学模式初探

黄 吉 聪

(厦门华天涉外职业技术学院，福建 厦门 361102)

高等数学是高职高专各专业必修的一门重要基础课和工具课，其核心内容是微积分(本文将以微积分作为研究讨论的内容)。笔者及多位同仁在多年的高职高专的高等数学教学实践中发现，传统“重理论、轻应用”的高数教学模式几乎要把本课程教学逼近死胡同，因此，倡导并设计一种以应用为导向、与各专业知识相结合的有用、易理解的高等数学教学模式显得尤为重要。

1 问题提出

1.1 传统“重理论、轻应用”的高等数学教学模式的弊端

传统“重理论、轻应用”的高等数学教学模式侧重于讲授相关的数学概念、性质、方法及运算，其对发挥本课程的“思维体操”作用，训练学生的抽象理解、逻辑推理、数学运算等思维能力有着不可替代的作用。但不可否认的是，思维的训练是一个循序渐进、潜移默化的过程，是一个一下子看不出有无效果的学习活动；而且思维能力提高了多少，也是很难去评价衡量，很难看得到摸得着的。

1.2 传统“重理论、轻应用”的高等数学教学模式的后果

通过高等数学相关概念、性质、方法及运算的学习来达成思维训练的目的，由于思维有无提高、提高了多少不好评价衡量，其结果就是在十年多一点的高职高专高等数学的教学实践中，高等数学的作用一年比一年受到质疑，地位一年不如一年：几乎各专业的高等数学课时不断受到压缩，近两三年来，有些经济管理专业比如会计、会审、国商、电商等直接砍掉不开设了；即使有开设本课程的专业在人才培养方案制订时，也一直犹豫质疑——高等数学对人才培养、对专业教学有无作用？有无开设的必要？需要开设多少呢？

2 问题分析

教育部印发的教高〔2000〕2号文件——《教育部关于加强高职高专教育人才培养工作的意见》中指出：“课程和教学内容体系改革是高职高专教学改革的重点和难点。要按照突出应用性、实践性的原则重组课程结构，更新教学内容。要注重人文社会科学与技术教育相结合，教学内容改革与教学方法、手段改革相结合。教学内容要突出基础理论知识的应用和实践能力培养，基础理论教学要以应用为目的，以必需、够用为度；专业课教学要加强针对性和实用性。”

高职高专高等数学目前的教学困境，主要是由于课程本身的抽象性和教学实践抽象化、理论化所致。高等数学的教学在高职高专各专业教学中还是有着很广泛的用途的：在经济管理专业中主要涉及经济函数、利率极限、边际分析、弹性分析、最值分析等；在物流管理专业中主要涉及最值分析、库存模型等；电子相关专业中主要涉及拉氏变换与逆变换等；机械机电模具数控等专业中主要涉及质点运动分析、电子电容电路分析等。

高职高专高等数学的教学必须要贯彻“以应用为目的”基础课程教学要求，做到与各相关专业课程教学相结合，从而在对学生思维训练的同时，让学生学有实得、学有实用，让学生明白为什么而学本课程。因此，倡导并构建“以应用型案例教学为导向，应用教学与思维训练相结合”的高职高专高等数学教学模式就具有非常现实的意义。

3 模式构建

3.1 传统“重理论、轻应用”的教学模式

教材模式直接决定教学模式。笔者参阅了大量国内近十年出版的高职高专高等数学教材，并且听了多所高职高专院校高等数学老师的上课实践，发现所有的教学模式几乎都是“重理论”型的：整节课、整门课从头到尾都是在教授数学概念、性质、方法及运算，较少或几乎没有涉及相关数学内容的应用。其教学内容和教学模式如下：

(1) 整门课的教学内容及逻辑顺序。

(2)各节课的教学内容及教学模式。

①集合：集合定义→集合类型→集合性质→集合关系→集合运算→练习；

②函数：函数定义→函数要素→函数特性→函数类型(初等函数)→练习；

③极限：极限定义→极限运算→练习；

④导数：2个引例→导数定义→导数公式求导→导数运算(定义法、求导法则)→练习；

⑤不定积分：不定积分的定义→不定积分运算(换元法、分部积分法)→练习；

……

由上不难看出，所有教学内容和教学模式都侧重于数学概念、性质、方法及运算的教与学，看不出一点实际和专业方面的应用，这样的教学内容和教学模式最终都不可避免地引起大多数学生的排斥。

3.2 以应用型案例教学为导向，应用教学与思维训练相结合”的高职高专高等数学教学模式

此教学模式的逻辑顺序为：以应用型案例为先导(让学生有直观感知、理解)→引出相关数学内容→相关数学内容教学(结合大量应用型案例)→练习(纯数学练习与应用型案例练习相结合)。

下面我们以极限的教学讲授为例：

首先，我们先以两个日常生活中的例子来引出和介绍极限，以让学生有直观的认识。

引例1：【熟练工的工时数】生产同一产品，熟练工所需的工时数比新手要少。因为当你不断重复地做同一种工作时，你的操作方法会不断得到改善，操作时间慢慢地减少并逐渐接近于一个确定的时间。

分析：第一步，让学生直接感知；

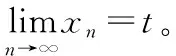
引例2：【日取锤半问题】一尺之锤，日取其半，万世不竭，所余趋零。这个问题说的是，有一把一尺长的锤子，一天取一半，永远取不完，但所余却不断减少，逐渐趋于零。

分析：第一步，让学生直接感知：

第二步，引入数学符号、数学概念：

总结：根据上面的两个引例，我们直观感知了极限的含义及思想方法，进而我们就可引入数列极限的概念。

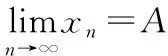
在明确了数列的极限的含义之后，我们就可继续引入一些更专业更实用的例子。

例3：设有一人有本金100元存入银行，年利率是12%，若以复利计息，则一年后本息共多少钱？

分析：这是一个简单的银行计算本息的指数运算，本息A1=100×(1+12%)=112元。

例4：同上例问，

分析：从上面两个例子不难看出，随着一年中计息次数不断增加，本息的总和也在不断增加；那么我们不禁要问，如果一年中计息次数不断增加，本息总和也会无限增加吗？

例5：设有一笔本金A0存入银行，年利率为r。若以复利计息，一年计息n次，则1年后本息An共多少钱？

讲完了上面3个有关极限的思想和方法的例子之后，我们就可让学生独自用极限的思想和方法来完成一个实用例子的求解。练习如下：

练习1：我们大家都知道半径为r的圆的面积s=πr2，可这个圆的面积公式是如何得来的呢？

我国晋代数学家刘徽曾用他创造的“割圆术”计算圆的面积，他采用圆内接正多边形的面积作为圆面积的近似值。在现在，按照极限的观点，当圆内接正多边形的边数无限增多时，正多边形的面积就无限接近于圆的面积。请根据“割圆术”的这一思想，推导圆的面积公式的由来。

总结：做完这一练习后，学生们就会对极限的思想、方法及其应用有了一个比较深入的理解；然后，我们就可适时地引入极限相关的性质及运算了。

例6：求下列数列的极限

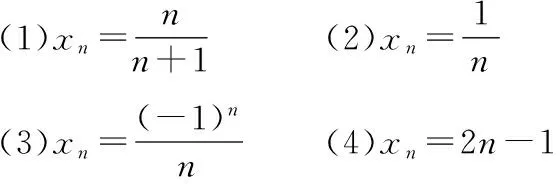
(5)xn=(-1)n+1(6)xn=1

以此类推，在教学讲授函数极限、导数、微分、不定积分、定积分、多元微积分时，一定要坚持以应用型案例教学为导向，坚持应用教学与思维训练并重，用应用案例引入把握相关数学概念、方法，用相关数学概念、方法、运算加强专业应用案例的分析与解决。

4 结论

“以应用型案例教学为导向，应用教学与思维训练相结合”的高职高专高等数学教学模式的倡导、构建与实践有着非常现实的意义，它让学生在进行思维训练的同时，也明白了高等数学这门基础理论课程对高职高专各相关专业教学的重要作用。但在这种模式的切实教学实践中发现，由于任课教师专业知识的缺乏，致使高等数学与各相关专业的结合远远不够，相关数学知识的应用型案例的数量、质量都远远不能满足教与学的需要，今后任课教师一定得加强和各专业教师的合作，并对各专业不断深入学习研究，借此，不断发掘、提炼、充实高等数学应用型教学案例。相信经过一定阶段的积累，有了充足的、高质量的应用型教学案例的支持后，我们所倡导和构建的应用型教学模式就会日益显现出其巨大的作用与价值。

[1]戴维R.安德森，丹尼斯J.斯威尼，基普·马丁.数据、模型与决策[M].北京：机械工业出版社，2009.

[2]侯风波，潘晓伟.高等数学[M].上海：上海大学出版社，2009.

[3]张国勇.高等数学[M].北京：高等教育出版社，2007.

[4]潘凯.高等数学[M].北京：中国科学技术大学出版社，2004.

[5]冯超玲，卢勇威.高等数学简明教程(工程技术类)[M].北京：北京理工大学出版社，2010.

[6]庄兴无，黄建华.高等数学(商务经济类)[M].北京：北京理工大学出版社，2009.

[7]毛骏健，顾牡.大学物理学[M].北京：高等教育出版社，2006.

[8]顾永杰.电工电子技术基础[M].北京：高等教育出版社，2005.

[9]姜启源.数学模型[M].北京：高等教育出版社，1993.

[10]郭培俊.高职数学建模[M].杭州：浙江大学出版社，2010.

[11]郑荣奕.对高职院校高等数学教学模式的探讨[J].邢台职业技术学院学报，2006,23(3).

[12]吴建祥，王瑜.浅谈高职院校高等数学教学模式改革的探索[J].中国科教创新导刊，2011，(14).

[13]曹勃.应用数学[M].成都：西南交通大学出版社，2010.