非线性单纯形蚁群算法在垃圾运输问题中的应用
2011-01-18向长城
李 舟,向长城
(湖北民族学院 理学院,湖北 恩施 445000)
随着我国城镇化和工业化的不断推进,越来越多的人涌入城市,由此而产生的各种垃圾对生态环境及人类生存带来极大的威胁,成为重要的社会问题.城市垃圾自其产生到最终被送到处置场处理,需要环卫部门对其进行收集与运输.而如何合理的进行垃圾运输,成为城市管理者的问题.收运过程为:某城市有多个行政区,每个区内均有一个车库,假设某一车库拥有最大装载量为w的垃圾收集车k辆,并且该区的垃圾收集点(待收集垃圾的点)有n个,该城市共有垃圾中转站p座.每天k辆垃圾车从车库出发,经过收集点收集垃圾,当垃圾负载达到最大装载量时,垃圾车运往中转站,在中转站卸下所有收运的垃圾,然后再出站收集垃圾,如此反复,直到所有收集点的垃圾都被收集完,垃圾车返回车库.如何安排垃圾收运车的收运路线,使在垃圾收运车的行车里程尽可能的少,是一个NP难题.
20世纪90年代初,由意大利学者Dorigo、Maniezzo根据真实蚂蚁的觅食行为首先提出来了蚁群算法[1-2],是一种应用于优化问题的启发式随机搜索算法.众多的研究结果表明,蚁群算法具有较强的发现较好解的能力[3],但是对于大规模计算问题,该算法需要花费很长的时间,并且容易陷入早熟熟练.而城市垃圾运输优化问题,为了减少计算时间和增加蚂蚁的多样性,利用非线性单纯形算法和蚁群算法混合,改进算法性能[4-6].单纯形法的优点在于它是一种直接的搜索方法,计算效率很高,并且单纯形法容易得到局部最优,不能保证全局最优.但是蚁群算法擅长全局最优,陷入局部最优的可能性很小,算法代价相对较高[7-8].将两种算法的优缺点结合,设计新的算法用于解决圾场的运输问题.
1 数学模型的建立
一个城市有m个垃圾站,有k辆载重为Q的垃圾运输车,在遍历收集点且不重复的前提下使其路径最短.其优化模型如下:
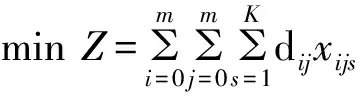
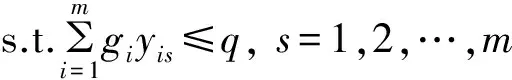
其中:gi表示第i点的垃圾量(i=2,3,4…,276);(xi,yi)表示序号为i的收集点的坐标;dij表示从垃圾收集点i到垃圾收集点j的距离;Q表示每辆车的载重量;k表示运输车数目;m表示收集点数目.
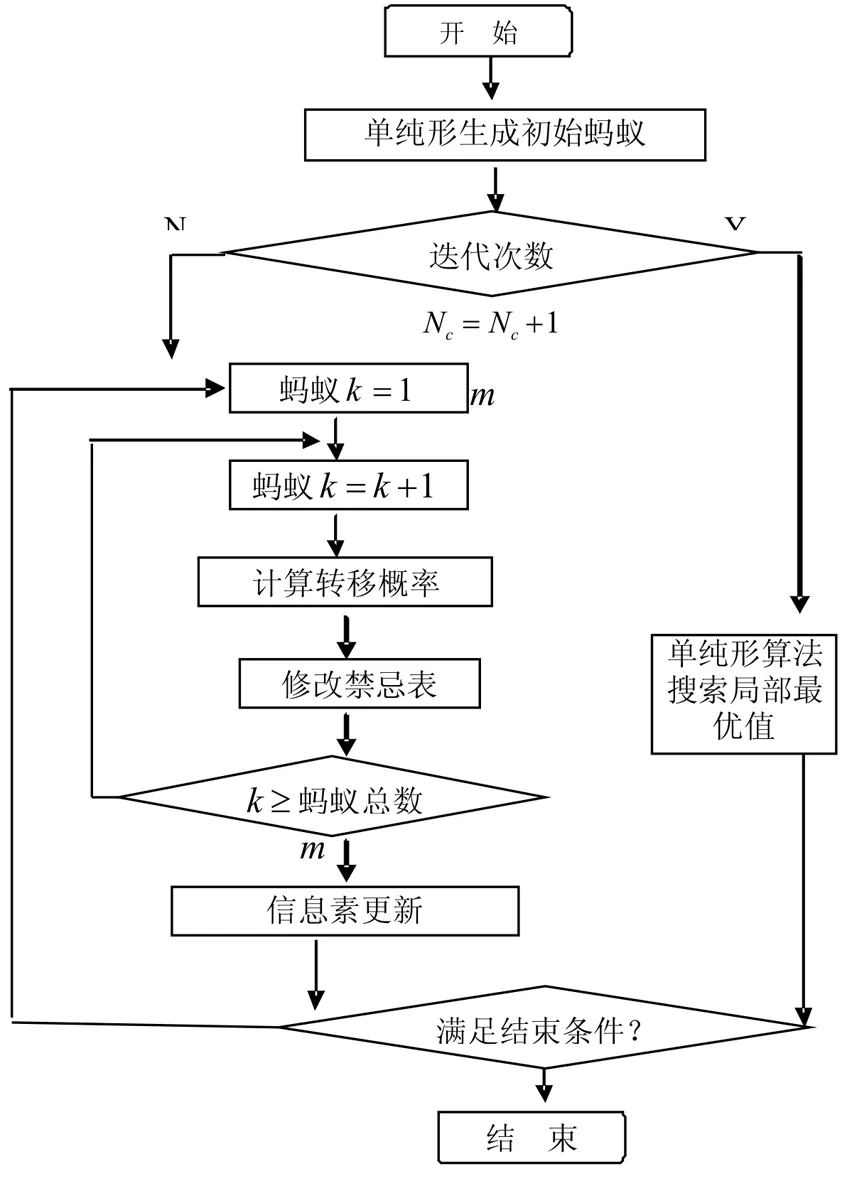
图1 算法流程图 Fig.1 Algorithm flow chart
2 非线性单纯形蚁群算法
垃圾运输问题相当于将k只蚂蚁随机放到n个全连通的城市上,当所有蚂蚁都遍历完n个城市以后,计算出此次遍历的最短路径.由于蚂蚁算法的局限性,把单纯形算法结合起来,设计新的算法用于解决该类问题.
对于N维问题,需要N+1个单纯形的顶点产生一个N维空间的单纯形.单纯形的算法的基本流程为:
step1: 求出目标函数值最小顶点、次小顶点和最大顶点;
step2: 计算出最小顶点的之外的N个顶点的形心点;
step3: 计算出最大顶点关于形心点的反射点;
step4: 计算反射点的目标函数值,若大于次小顶点,则在该方向上执行一次收缩;若小于最大顶点值,则执行一次扩张;
step5: 单纯形整体接近最低点,执行下一次迭代.
为了充分利用单纯形算法的局部搜索能力和蚁群算法的全局搜索能力,在蚂蚁初始生成的时候采用单纯形算法进行初始生成,避免了过去均匀生成初始蚂蚁的缺点.
在进入迭代搜索的时候,首先利用蚁群算法进行目标函数优化.对迭代次数进行设置,当蚁群算法搜索到后期的时候,每隔10代进行一次单纯形搜索,可以避免搜索时间过长,然后继续进行蚁群搜索,图1为该算法的流程图.
为了验证算法,选用f=1+x*sin(4πx)-y*sin(4πy+π),x,y∈[-1,1]进行测试,改函数为变峰、多变量多极值点的函数,图2为该算法的相关性能比较,其中(a)函数初始分布蚂蚁图,(b)为蚂蚁算法搜索的最终蚂蚁分布图,(c)为单纯形蚂蚁算法的最终分布,(d)为算法收敛曲线.


(a)蚂蚁初始位置分布,(b)蚂蚁算法最终位置分布,(c)单纯形蚂蚁算法最终位置分布,(d)单纯形蚂蚁算法收敛曲线图2 测试函数性能比较图Fig.2 Performancecomparison test function
3 数值试验及仿真
垃圾车的最大装载量:200.0(yards)每辆垃圾车每天的负载总量:2200.0(yards).每辆垃圾车每天最多经过的垃圾收集点个数:500,Stop_ID:收集点编号,X,Y分别为该点的坐标,单位:feet;Load:该点的垃圾量,单位:yard;Stop_Type:收集点类型(0:车库,1:垃圾收集点,2:中转站).见参考文献[9].其中图3为用单纯性蚂蚁算法对垃圾运输分类问题进行仿真计算,该算法很好的完成最短路径搜索,并且在50代左右就达到了最优路径,减少了计算量.12(5):4-8.
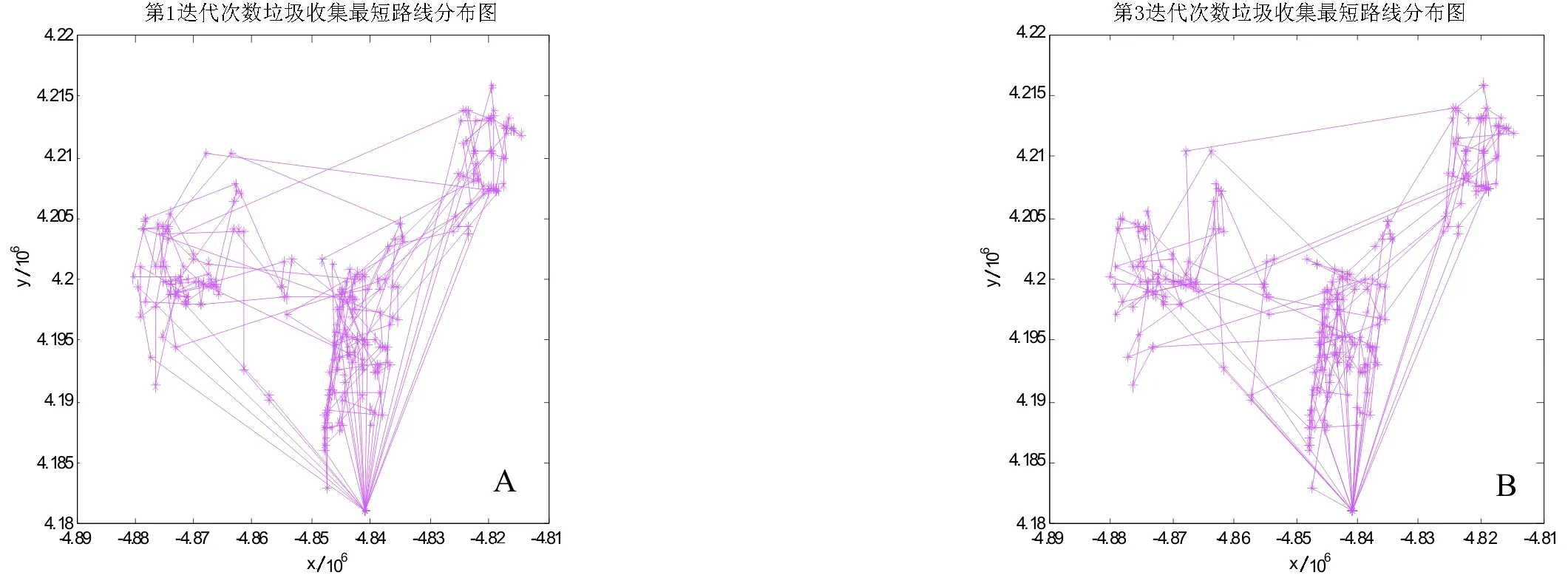
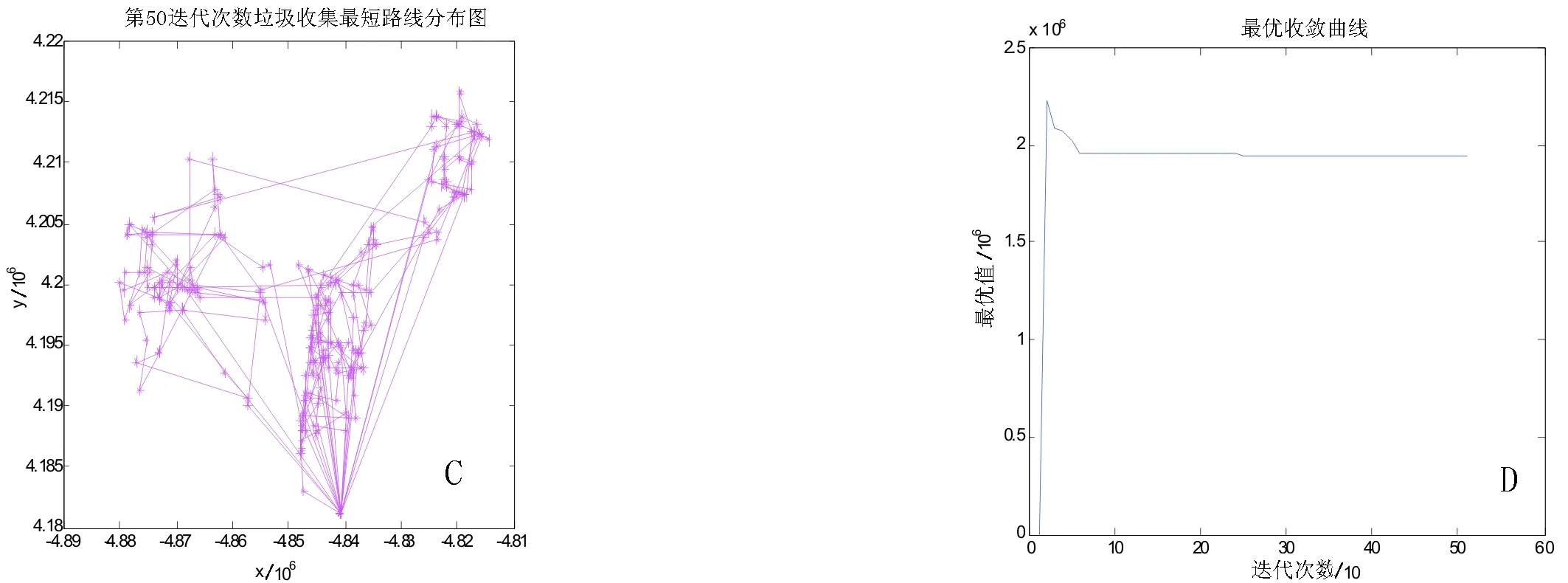
图3 垃圾运输最终线路Fig.3 Final transport routes of garbage
[2] 王家葵,王一涛.续断的本草考证[J].中药材,1991,14(5):44-47.
[3] 陈翠,杨丽云,赵菊,等.续断高产栽培技术[J].现在农业科技,2007(23):150-152.
[4] 丁莉,武芸.五鹤续断部分生物学特性及栽培管理研究[J].湖北民族学院学报:自然科学版,2005,23(2):144-146.
[5] 武芸,丁莉,周吉源.五鹤续断的研究概况与开发前景[J].湖北民族学院学报:医学版,2004,21(4):31-33.
[6] 中国医学科学院药物研究所.中药志(第2册)[M].北京:人民卫生出版社,1982:536.
[7] 钟美英,申玉华.续断的研究现状[J].中医药导报,2008,14(6):137-138.
[8] 丁莉,李慧,武芸,等.药用川续断的研究进展[J].湖北民族学院学报:自然科学版,2010,28(3):320-324.
[9] 唐丽,刘友全,钟秋平.南天竹超氧化物歧化酶同工酶的研究[J].中南林业科技大学学报,2008,28(3):55-59.
[10] 陈彦云.不同地区罗布红麻和罗布白麻的过氧化物同工酶分析[J].安徽农业科学,2010,38(12):6092-6094.
[11] 李学强,李秀珍,王祥.5种樱桃属植物的POD、CAT和SOD同工酶分析[J].生物学通报,2010,45(2):46-48.
[12] 周正贵,王燕萍,吴丽莉,等.白三叶幼苗抗氧化酶类的电泳研究[J].贵州农业科学,2008,36(1):43-45.
