地面沉降变形非线性完全耦合数学模型
2011-01-16李培超
李培超
(上海工程技术大学机械工程学院,上海 201620)
地面沉降变形非线性完全耦合数学模型
李培超
(上海工程技术大学机械工程学院,上海 201620)
基于多孔介质有效应力原理的渗流-变形耦合,考虑孔隙度、渗透率非线性变化,建立三维地面沉降变形完全耦合数学模型,并给出了模型的有限差分解法.该模型可以刻画地下水开采、建筑物荷载、基坑降水等作用下的三维地下水渗流场和地层变形位移场,分析地面沉降的三维变化与非线性特征,为地面沉降研究与防治提供技术手段.
地面沉降;有效应力原理;流固耦合;三维位移场;非线性变化模型;有限差分法
因地下流体(如地下水、石油天然气、地热等)过量开采而导致的地面沉降,已成为目前全球面临的比较严峻的环境地质灾害问题[1].长江三角洲是我国地面沉降最严重的地区之一.因开采地下水,上海于1921年就已发现地面沉降现象,截至2005年地面沉降已达2.6m[2].地面沉降作为缓变型地质灾害,不仅会造成巨大的危害和经济损失,而且还会对未来工程建设构成潜在的隐患和威胁,影响人们的生产和生活.
数学模型法作为地面沉降预测评价最重要的手段之一,一直是国内外学术界密切关注的研究领域.本文尝试建立基于多孔介质有效应力原理的非线性地面沉降变形完全耦合数学模型,并给出其有限差分解法.
1 地面沉降完全耦合数学模型研究概述
1.1 完全耦合模型研究现状及分析
按照地下水渗流模型和土体变形模型结合形式,地面沉降数学模型可分为三大类:两步走模型、部分耦合模型和完全耦合模型[3].
完全耦合模型的理论基础是Biot三维固结理论[4],其假设孔隙水与土体颗粒不可压缩以及水流符合达西定律,根据有效应力原理、土的连续性方程和应力平衡方程并结合地下水流方程,推导建立了三维固结理论,奠定了多孔介质流固耦合渗流理论的基础.
在求解地面沉降方面,Lewis等[5]以此为基础提出完全耦合模型,并运用于威尼斯的地面沉降计算中,结果表明水头下降和地面沉降比两步计算较快地趋于稳定.Tarn等[6]分析了各向异性多孔介质因点汇导致的地面沉降.His等[7-8]用完全耦合模型分析了在有潜水的含水地层中抽取地下水引起的地面沉降问题.近年来国内也开展了地面沉降完全耦合模型的研究,陈杰等[9]运用Biot二维固结有限元程序计算了某长江公路大桥桥位区因长期过量开采地下水而引起的地面沉降.骆祖江等[10]以Biot三维固结理论为基础,引用孔隙度、渗透率非线性动态变化模型[11-12],利用有限元方法,模拟了上海市第四纪松散沉积层某深基坑降水引起的地面沉降问题.
以上完全耦合模型,虽然一般都以Biot三维固结理论为基础,但实际上关注和计算的还是垂向沉降,而对水平位移基本上没有分析和讨论.而实际上地面变形是三维的,其水平位移通常是存在的,而且也相当重要.许多现场量测结果表明,地下水抽取引起地面沉降的同时,也会引起地层的水平位移,有些地方还伴有地裂缝的出现.地面建筑物出现倾斜倒塌以及地裂缝的形成,除与地面沉降不均匀性有关外,还可能与水平位移及水平应力密切相关[13].
油气开采同样会诱发地面沉降和变形[14-15],严重时会导致套管损坏,甚至油井报废[16].油田统计资料证实大部分套管发生错断剪切破坏,这可能是因岩体发生水平错动而致.田杰等[17]基于流固耦合渗流理论,分析了采油过程岩体的变形,指出采油过程中孔隙压力消散,有效应力增加,水平位移不断加大,采油层受压剪作用易发生套损.
除地下水开采外,近年来大规模的工程建设已成为地面沉降新的影响因素.以上海为例,因工程建设量大,而浅层又是软黏土层,所以地面沉降原因已由单纯的开采地下水转向开采地下水和城市建设活动双重因素[18],而且在当前微量沉降阶段,工程建设及运行所引起的地面沉降占总沉降的权重显然会越来越大.通常一维固结模型假设荷载是常数,因此它无法描述工程建设对地面沉降的影响.龚士良[19]分析了软黏土的微观结构性质对于浅层沉降的影响,而唐益群等[20]则从模型试验角度研究了高层建筑群对地面沉降的影响效应.
1.2 完全耦合模型的发展方向
如上文所述,地面沉降变形通常具有三维特征,而并非只体现为垂向沉降,水平位移同样占有重要的地位.此外,当前工程建设对于地面沉降的影响权重越来越大,因此只有采用三维土体变形理论才能更好地描述地面变形的三维特征和复杂荷载的影响.
因地下流体开采(包括基坑降水)或地面建筑物荷载作用所诱发的地面沉降,其机理是类似的,即随着孔隙水压力消散,有效应力增大,土体产生压缩变形,进而表现为土层表面的位移;土体的变形同时又会导致孔隙度和压缩系数、渗透系数等发生变化,从而影响地下水的渗流特征.可见地面沉降是一个水-土相互作用的过程,属于典型的多孔介质流固耦合问题,因此从理论上说,应采用多孔介质流固耦合渗流模型描述和分析地面沉降,换言之,只有使用完全耦合模型才能更好地刻画地面沉降过程的流固耦合物理实质.
将以上二者结合建立地面沉降变形的三维完全耦合模型,并进行三维变形和渗流耦合分析是非常必要的,也是当前地面沉降模型应深入研究和发展的方向[3].
2 基于多孔介质有效应力原理的完全耦合数学模型
2.1 基于多孔介质有效应力原理的流固耦合渗流模型
文献[21]从渗流力学角度出发,解析导出了基于多孔介质的有效应力原理,其形式[21-22]为

在流固耦合渗流研究领域,笔者引进该有效应力原理,以代替经典Terzaghi有效应力原理,建立了完备的多孔介质流固耦合渗流数学模型[12,23],并进一步对该模型开展了工程应用研究[24-26].结果表明经典Terzaghi一维固结理论及Biot三维固结理论是该模型的简化和近似[12,25].该模型不仅采用了基于多孔介质的有效应力原理,而且考虑了孔隙流体和固体颗粒的压缩性,并且包含了多孔介质孔隙度和渗透率的非线性动态变化模型,而Biot固结模型推导过程中忽略了孔隙水和土体颗粒的压缩性,采用了定水力参数.而如前文所述,地面沉降过程正因为是典型的流固耦合过程,所以土层参数和水文地质参数实际上呈现随土体变形而变化的非线性特征,而非保持常数.
2.2 地面沉降完全耦合数学模型
下面以饱和多孔介质流固耦合渗流数学模型[12]为基础,建立饱和土体地面沉降完全耦合数学模型.
2.2.1 控制方程组
2.2.1.1 应力场平衡方程
应力场平衡方程为

式中Fi为作用在土体上的体积力.
联立式(1)和式(2),得到以土体有效应力和孔隙水压力表示的应力场方程:

土体骨架本构关系:

式中:Dijkl——劲度矩阵,可以为弹性矩阵,也可是弹塑性矩阵等,由土体本构关系决定;εkl——应变张量.目前较常用的土体本构方程有修正剑桥模型和邓肯-张模型等.为描述简单起见,假定土体骨架为各向同性线弹性体,则有

其中λ,εV和G分别为土体的Lame系数、骨架体积应变和剪切模量,且满足

式中:E——土体杨氏模量;ν——泊松比;Wx,Wy,Wz——土体骨架x,y,z方向的位移.几何方程(假定土体符合小变形假设):

将式(5)代入式(3)并结合式(7),得到位移场方程组:

如只考虑土体自重,则式(8)可简化为

其中 γ=[(1- φ)ρs+ φ ρw]g,ρs和 ρw分别为土体颗粒密度和孔隙水密度.
2.2.1.2 渗流场方程
考虑孔隙水和土体颗粒的压缩性,假设二者体积弹性压缩模量分别为Kf,Ks,设土体渗透率张量为K,三向主渗透率依次为kx,ky,kz,参考文献[12]的推导方法,可给出压力场方程:

假设土体渗透率各向同性,式(10)简化为

式中:k——各向同性渗透率;h——高度.如忽略重力影响,有
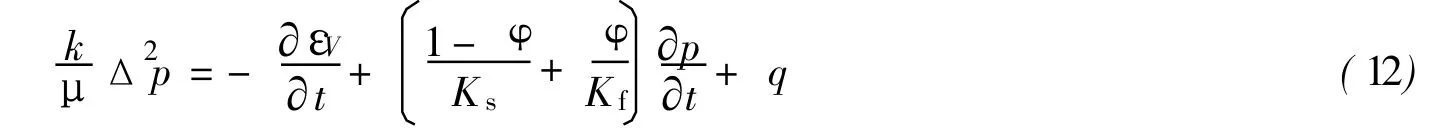
式中q代表源汇项.
2.2.1.3 孔隙度渗透率非线性变化模型
地面沉降属典型的水-土耦合渗流过程.孔隙水压力的变化,会引起土体骨架有效应力的变化,进而导致孔隙度、渗透率等的变化,同时这些变化又反过来影响孔隙水的流动和压力的分布.根据固结系数的定义,它与渗透率、压缩系数直接相关,而贮水系数则与孔隙度、压缩系数等有直接的换算关系[27],因此在地面固结沉降过程中,土层参数和水文地质参数都是动态变化的,这已经被人们所认识和接受[10-12,25,27-29].
文献[12]充分考虑流固耦合作用,建立了物性参数动态变化模型,其中孔隙度非线性模型如下:
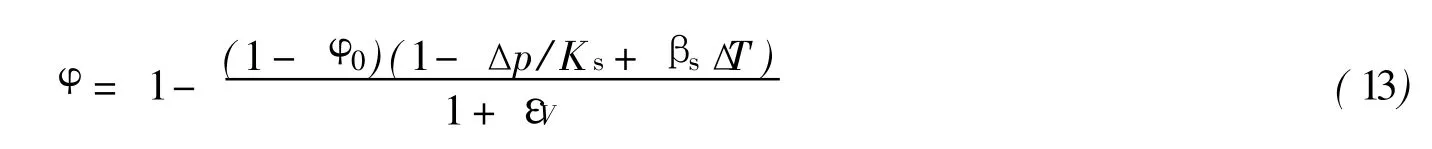
式中:φ0——土层初始孔隙度;βs——土体热膨胀系数.如果忽略温度场效应,则式(13)简化为

根据渗流力学Kozeny方程,可导出渗透率_的变化模型为

式中k0为初始渗透率.
式(9)、式(12)和式(14)构成地面沉降控制方程组,该方程组共有5个方程,而求解变量为Wx,Wy,Wz,φ,p,总计5个,可见方程组是封闭的.
2.2.2 定解条件
对于上述控制方程组,应补充适当的边界条件和初始条件,才能构成定解问题.
2.2.2.1 初始条件
通常指初始时刻土层孔隙水压力和位移场的原始分布.渗流场、位移场和孔隙度初始条件分别为

式中:p0——原始地层孔隙水压力分布;W0——土体初始位移,可取为0.
2.2.2.2 边界条件
通常较常用的渗流场边界条件有第一类和第二类边界条件,即孔隙水压力满足定压或定流量边界条件.定压边界条件和定流量边界条件(忽略重力效应)分别为

式中:pb——边界 Γ上的孔隙水压力;n——边界 Γ的法向量;q——边界 Γ已知流量.
同理,位移场边界条件也可给出如下(以第一类边界条件为例):

式中Wb为边界 Γ上的已知位移矢量.
然而对于地面沉降问题,所涉及土层区域内位移场边界条件可能难以直接给出.为此,可采用“扩展法”[15],将研究区域取得足够大,如拓展至自然边界(固壁边界),即可给出位移场边界条件[26]:

式中 Γ1为扩展后的“计算区域”所对应的边界.
至此,控制方程组(式(9)、式(12)和式(14))以及定解条件(式(16)~(20)和式(22))即构成地面沉降变形非线性完全耦合数学模型,对于此数学模型,可采用有限差分、有限元等数值方法求解.
3 模型数值解法
此处给出模型的有限差分解法.
a.给定初始时刻的孔隙度、渗透率和孔隙水压力等.
b.结合给定的压力场和位移场边界条件及上述时刻的孔隙度、渗透率等,先采用全隐式有限差分法将方程(9)和(12)离散为相应的代数方程组,然后再利用强隐式(SIP)联立迭代法对上述方程组求解,从而计算出第1个时间步的三向位移和孔隙水压力.
c.将第1个时间步的三向位移和孔隙水压力代入方程(14),得出第1个时间步的孔隙度分布;再代入方程(15),得到与孔隙度对应的渗透率分布.
d.利用第1个时间步的孔隙度和渗透率以及位移场和压力场,返回b,重复上述过程,便可得到第2、第3……即不同时间步的结果,直到计算结束.
4 结 语
本文建立了地面沉降变形的非线性三维完全耦合数学模型,它充分考虑了地面沉降过程的流固耦合物理实质,是对Biot固结理论的合理改进和完善.它可以计算地下水开采或建筑物荷载作用下的三维位移场和渗流场,并分析地面沉降、水平位移及压力场之间的相互影响和作用.在数值方法方面,采用全隐式有限差分法离散控制方程,该方法简单易懂;并采用强隐式联立迭代法求解离散后的方程组,该迭代方法效率较高,适合于三维问题大型稀疏方程组的求解.
下一步可针对区域性地面沉降或具体工程地面沉降,首先对上述三维模型进行验证和标定,反演求得更为准确的土层参数和水文地质参数,再进一步用于地面沉降的预测和模拟,从而更加全面和深入地认识地面沉降变形的三维变化与非线性特征.
[1]GAMBOLATI G,TEATINI P,FERRONATO M.Anthropogenic land subsidence[J].Earth Science Frontiers,2006,13(1):160-178.
[2]XUE Yu-qun,Z HANG Yun,YE Shu-jun,et al.Land subsidence in China[J].Environmental Geology,2005,48:713-720.
[3]张云,薛禹群.抽水地面沉降数学模型的研究现状与展望[J].中国地质灾害与防治学报,2002,13(2):1-6.(ZHANG Yun,XUE Yu-qun.Present situation and prospect on the mathematical model of land subsidence due to pumping[J].The Chinese Journal of Geological Hazard and Control,2002,13(2):1-6.(in Chinese))
[4]BIOT M A.General theory of three-dimensional consolidation[J].Journal of Applied Physics,1941,12:155-164.
[5]LEWIS R W,SCHREFLER B.A fully coupled consolidation model of the subsidence of Venice[J].Water Resource Research,1978,14(2):223-230.
[6]TARN J Q,LU C C.Analysis of subsidence due to a point sink in an anisotropic porous elastic half space[J].International Journal for Numerical andAnalytical Methods in Geomechanics,1991,15(4):573-592.
[7]HIS JP,CARTER J P,SMALL J C.Surface subsidence and drawdown ofthe water table due to pumping[J].Geotechnique,1994,44(3):381-396.
[8]SU M B,SU C L,CHANG C J,et al.A numerical model of ground deformation induced by single well pumping[J].Computer and Geotechnics,1998,22(2):39-60.
[9]陈杰,朱国荣,顾阿明,等.Biot固结理论在地面沉降计算中的应用[J].水文地质工程地质,2003,30(2):28-31.(CHEN Jie,ZHU Guo-rong,GU A-ming,et al.Application of Biot onsolidation theory to calculation of land subsidence[J].Hydrogeology and Engineering Geology,2003,30(2):28-31.(in Chinese))
[10]骆祖江,刘金宝,李朗.第四纪松散沉积层地下水疏降与地面沉降三维全耦合数值模拟[J].岩土工程学报,2008,30(2):193-198.(LUO Zu-jiang,LIU Jin-bao,LI Lang.Three-dimensionalfull coupling numerical simulation of groundwater dewatering andlandsubsidence in quaternary loose sediments[J].Chinese Journal of Geotechnical Engineering,2008,30(2):193-198.(in Chinese))
[11]冉启全,李士伦.流固耦合油藏数值模拟中物性参数动态模型研究[J].石油勘探与开发,1997,24(3):61-65.(RAN Q-i quan,LI Sh-i lun.Study on dynamic models of reservoir parameters in the coupled simulation of multiphase flow and reservoir deformation[J].Petroleum Exploration and Development,1997,24(3):61-65.(in Chinese))
[12]李培超,孔祥言,卢德唐.饱和多孔介质流固耦合渗流数学模型[J].水动力学研究与进展:A辑,2003,18(4):419-426.(LI Pe-i chao,KONG Xiang-yan,LU De-tang.Mathematical modeling of flow in saturated porous media on account of fluid-structure coupling effect[J].Chinese Journal of Hydrodynamics,2003,18(4):419-426.(in Chinese))
[13]王庆良,刘玉海,陈志新,等.抽水引起的含水层水平应变-地裂缝活动新机理[J].工程地质学报,2002,10(1):46-50.(WANG Qing-liang,LIU Yu-hai,CHEN Zh-i xin,et al.Horizontal strainof aquifer inducedby groundwater pumping:a new mechanism for ground fissure movement[J].Journal of Engineering Geology,2002,10(1):46-50.(in Chinese))
[14]SETTARI A,WALTERS D A.Advances in coupled geomechanical and reservoir modeling with applications to reservoir compaction[J].SPE Journal,2001,6(3):334-342.
[15]GUTIERREZ M S,LEWIS R W.Coupling of fluid flow and deformation in underground formations[J].ASCE Journal of Engineering Mechanics,2002,128(7):779-787.
[16]FREDRICH J T,ARGUELLO J G,DEITRICK G L,et al Geomechanical modeling of reservoir compaction,surface subsidence,and casing damage at the Belridge Diatomite Field[J].SPE Reservoir Evaluation&Engineering,2000,3(4):348-359.
[17]田杰,刘先贵,尚根华.基于流固耦合理论的套损力学机理分析[J].水动力学研究与进展:A辑,2005,20(2):221-225.(TIAN Jie,LIU Xian-gui,SHANG Gen-hua.Casing damage mechanism based on theory of fluid-solid coupling flow through underground rock[J].Chinese Journal of Hydrodynamics,2005,20(2):221-225.(in Chinese))
[18]龚士良.上海城市建设对地面沉降的影响[J].中国地质灾害与防治学报,1998,9(2):108-111.(GONG Sh-i liang.Effects of urban construction on the land subsidence in Shanghai[J].The Chinese Journal of GeologicalHazard and Control,1998,9(2):108-111.(in Chinese))
[19]GONG Sh-i liang.The microscopic characteristics of Shanghai soft clay and its effect on soil body deformation and land subsidence[J].Environmental Geology,2009,56(6):1051-1056.
[20]TANG Y-i qun,CUI Z D,WANG J X,et al.Model test study of land subsidence caused by high-rise building group in Shanghai[J].Bulletin of Engineering,Geology and the Environment,2008,67:173-179.
[21]徐献芝,李培超,李传亮.多孔介质有效应力原理研究[J].力学与实践,2001,23(4):42-45.(XU Xian-zhi,LI Pe-i chao,LI Chuan-liang.Principle of effective stress based on porous medium[J].Mechanics and Engineering,2001,23(4):42-45.(in Chinese))
[22]李培超,孔祥言,李传亮,等.地下各种压力之间关系式的修正[J].岩石力学与工程学报,2002,21(10):1551-1553.(LI Pe-i chao,KONG Xiang-yan,LI Chuan-liang,et al.Correction of relationship among various underground pressures[J].Chinese Journal of RockMechanics and Engineering,2002,21(10):1551-1553.(in Chinese))
[23]李培超.多孔介质流固耦合渗流数学模型研究[J].岩石力学与工程学报,2004,23(16):2842.(LI Pe-i chao.Mathematical models of flow-deformation coupling for porous media[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(16):2842.(in Chinese))
[24]李培超,李贤桂,龚士良.承压含水层地下水开采流固耦合渗流数学模型[J].辽宁工程技术大学学报:自然科学版,2009,28(增刊 1):249-252.(LI Pe-i chao,LI Xian-gui,GONG Sh-i liang.Mathematical modeling of flow and land subsidence coupling for groundwater pumping in confined aquifer[J].Journal of Liaoning Technical University:Natural Science,2009,28(Sup1):249-252.(in Chinese))
[25]李培超,李贤桂,卢德唐.饱和土体一维固结理论的修正-饱和多孔介质流固耦合渗流模型之应用[J].中国科学技术大学学报,2010,40(12):1273-1278.(LI Pe-i chao,LI Xian-gui,LU De-tang.A modified form for the uniaxial consolidation theory in saturated soils:an application of mathematical models for flow-deformation coupling in saturated porousmedia[J].Journal of University of Science and Technology of China,2010,40(12):1273-1278.(in Chinese))
[26]李培超,李贤桂.二维有限饱和多孔介质流动变形耦合数值模拟[J].上海大学学报:自然科学版,2010,16(6):655-660.(LI Pe-i chao,LI Xian-gui.Numerical simulation of two-dimensional deformation and flow due to loading within a saturated finite poroelastic media[J].Journal of Shanghai University:Natural Science Edition,2010,16(6):655-660.(in Chinese))
[27]陈崇希,裴顺平.地下水开采-地面沉降模型研究[J].水文地质工程地质,2001,28(2):5-8.(CHEN Chong-xi,PEI Shun-ping.Research on groundwater exploitation-land subsidence model[J].Hydrogeology and Engineering Geology,2001,28(2):5-8.(in Chinese))
[28]庄迎春,刘世明,谢康和.萧山软粘土一维固结系数非线性研究[J].岩石力学与工程学报,2005,24(12):4565-4569.(ZHUANG Ying-chun,LIU Sh-i ming,XIE Kang-he.Study on nonlinearity of one-dimensional consolidation coefficient of Xiaoshan clay[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(12):4565-4569.(in Chinese))
[29]于军,吴吉春,叶淑君,等.苏锡常地区非线性地面沉降耦合模型研究[J].水文地质工程地质,2007,34(5):11-16.(YU Jun,WU J-i chun,YE Shu-jun,et al.Research onnonlinear coupled modeling of land subsidence in Suzhou,Wuxi and Changzhou areas,China[J].Hydrogeology and Engineering Geology,2007,34(5):11-16.(in Chinese))
A nonlinear fully coupled mathematical model for land subsidence
LI Pe-i chao
(College o f Mechanical Engineering,Shanghai University o f Engineering Science,Shanghai201620,China)
For seepage-deformation coupling in porous media based on the effective stress principle,a fully coupled 3D mathematical model for land subsidence was established with consideration of the nonlinear changes of soil porosity and permeability,and the finite differencemethodwas used to solve the model.The model can be usedto characterize the 3D groundwater seepage field and the stratum deformation displacement field with the effects of groundwater exploitation,construction loads,and dewatering of foundation pits,and to analyze the 3D changes and nonlinear characteristics of land subsidence.The model also provides technical approaches for research of land subsidence and its prevention and treatment.
land subsidence;effective stress principle;fluid-solid coupling;3D displacement field;nonlinear change model;finite difference method
P642.26;O357.3
A
1000-1980(2011)06-0665-06
10.3876/j.issn.1000-1980.2011.06.014
2010-12-03
上海高校选拔培养优秀青年教师科研专项基金(GJD09029);上海工程技术大学科技发展基金(校启09-27)
李培超(1976—),男,山东寿光人,副教授,博士,主要从事渗流力学研究.E-mail:wiselee18@163.com
