大跨度悬索桥的车桥耦合振动分析
2011-01-16逄焕平王建国
逄焕平, 王建国, 钱 锋
(1.合肥工业大学 交通运输工程学院,安徽 合肥 230009;2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
大跨度悬索桥的车桥耦合振动分析
逄焕平1, 王建国2, 钱 锋2
(1.合肥工业大学 交通运输工程学院,安徽 合肥 230009;2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
车桥耦合相互作用问题采用有限元法分析时是一个时变的线性动力系统。文章将时变的线性动力系统分解成时变的线性动力系统和时不变的线性动力系统的叠加,利用状态空间理论建立了车桥耦合振动有限元法分析的状态空间法,并对悬索桥在移动车辆作用下的车桥耦合振动问题进行了研究。
车桥耦合相互作用;时变线性动力系统;悬索桥
0 引 言
悬索桥的静动力计算问题是近年来研究的热点[1],很多学者都对桥梁在移动列车车辆荷载作用下的车桥耦合振动问题进行了研究。文献[2]对车桥系统空间振动进行了研究,在分析时分别对车辆和桥梁结构建立运动方程,两者之间通过轮对的接触力联系在一起,这种方法后来为各国研究人员采用。
文献[3]采用7个自由度的卡车模型对斜拉桥在移动车辆作用下的车桥耦合振动问题作了研究;文献[4]对斜拉桥在风和列车同时作用下的空间振动问题进行了分析;文献[5]提出了一种新的车桥耦合计算模型——车-轨-桥单元,为以后的研究提供了一种新的思路;文献[6]对建有输水管道的悬索桥在列车作用下的响应进行了研究;文献[7]对大跨度斜拉桥在移动荷载作用下的动力特性进行了研究;文献[8]对移动列车作用下,轨道不平顺对其动力特性的影响进行了研究;文献[9]对不同路面状况下桥梁的车桥耦合振动特性进行了研究。
本文推导了车桥耦合单元的影响矩阵,建立了有限元分析的状态空间法,给出了双轴移动车辆的车桥相互作用矩阵,详细讨论了车桥耦合运动方程的求解过程,对悬索桥在移动车辆作用下的动力响应问题进行了计算分析。
1 车桥耦合单元的推导
车桥耦合单元的模型如图1所示。

图1 车桥耦合单元
图1中车辆模型作用在第s个梁单元上,车辆移动速度为v。假定作用于车辆上的外荷载为F v,车辆模型的节点位移向量为 y,并且有:F v=F e+F c,其中,F e为作用在车辆模型上的外荷载;Fc为车桥之间的相互作用力。由图1可知,所有车辆模型的节点可分为2部分,车体部分对应的自由度用y u表示,车轮部分对应的自由度用 y w表示。假定作用在车轮和车体上的外荷载分别用F ew和F eu表示,车轮与梁单元之间的接触力用 f c表示,则对车辆按照车轮节点和车体节点进行分离,可以得到车辆的运动方程为:




(9)式即为车辆模型车桥耦合的运动方程。
2 移动双轴车辆作用下的车桥耦合单元
移动双轴车辆模型作用下的车桥耦合单元,如图2所示。
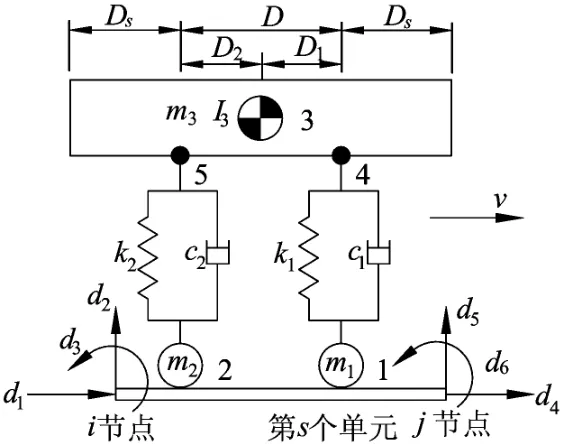
图2 移动双轴车辆作用下的车桥耦合单元


3 车桥耦合方程的求解
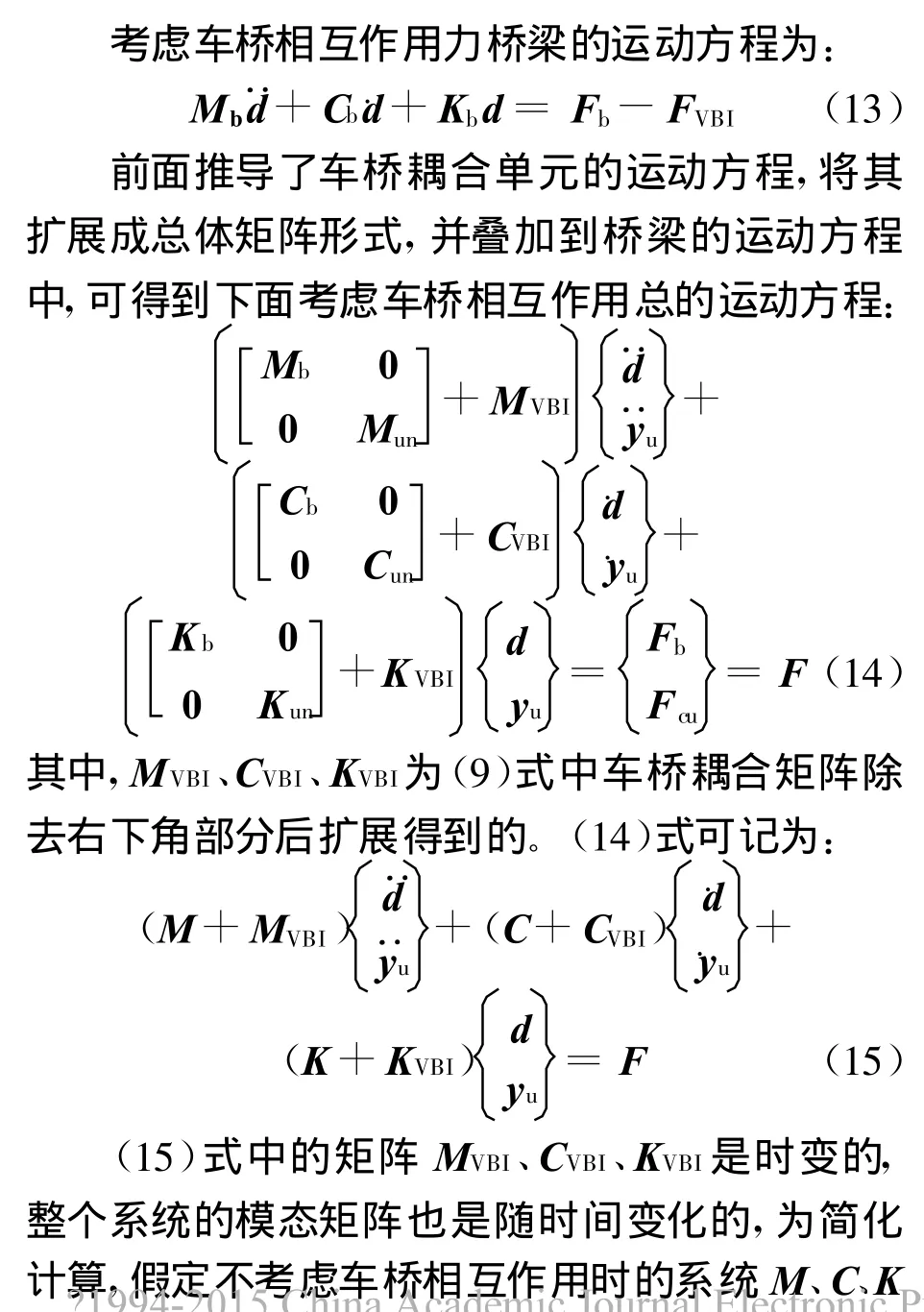

由(13)式可知,系统矩阵M、C、K包含2部分,分别是桥梁的系统和车辆的车体部分,因此模态矩阵Φ也分为桥梁的模态矩阵和车辆车体部分的矩阵。对于复杂模型,桥梁部分的模态矩阵可以通过大型通用软件Ansys计算得到,车体部分模型比较简单,其模态矩阵可以直接求得。通过Ansys导出的桥梁模态矩阵及计算得到的车体部分模态矩阵具有如下特征:ΦTMΦ是单位阵;ΦTKΦ是对角元素为ω2的对角矩阵;若采用阻尼比为ζ的比例阻尼,则 ΦTCΦ是2ζω的对角矩阵。
注意到上面的方程实际上是变质量、变刚度、变阻尼的系统,为方便求解,可将其转换为状态空间形式的方程,即
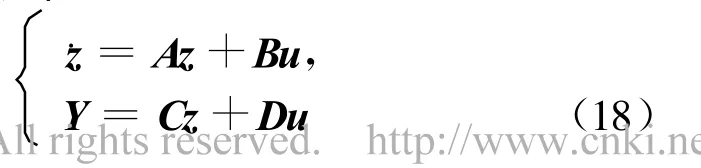
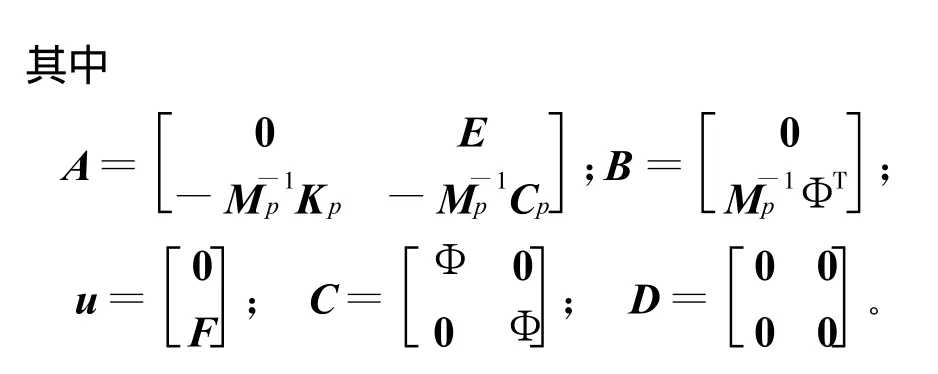
上述变质量、变刚度、变阻尼系统可以通过Matlab的系统仿真模块进行求解,可直接得到物理坐标系下各个点的位移响应。
4 算 例
本算例对某 360 m+1 080 m+1 080 m+360 m双主跨悬索桥在列车分别以速度100、200、300 km/h行驶时的车桥耦合问题进行了研究,其有限元网格划分如图3所示。
悬索桥参数见表1所列。
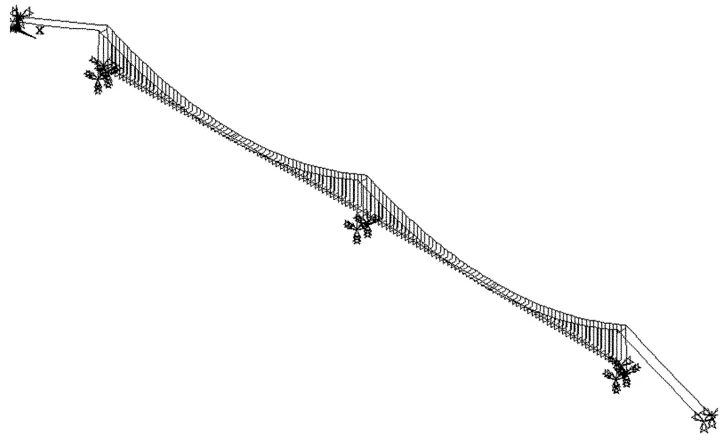
图3 某跨长江双主跨三塔悬索桥有限元网格划分图
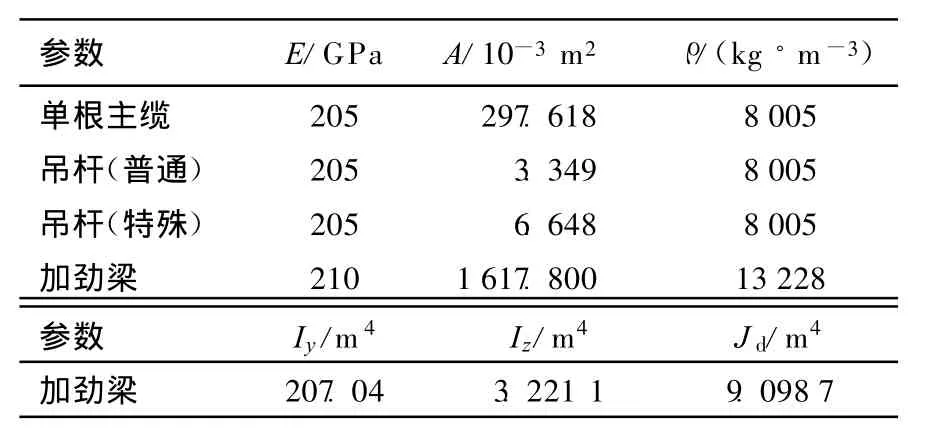
表1 主缆、吊杆和加劲梁的参数
列车由10节车厢组成,长度为250 m。每节车厢采用如图2所示的车辆模型。单节车厢的车体质量m3为32 000 kg,车体的转动惯量I3为197×104kg·m2,弹簧的刚度 k1、k2为 43×104N/m,阻尼 c1、c2为2×104N/m,车轮的集中质量m1、m2为 6 241 kg,车厢两车轮之间的距离D=2D1=2D2=19 m,车轮距车厢边缘的距离3m,一节车辆的长度为19+2×3=25 m。悬索桥的其它参数可参照文献[10]。
列车以3种速度行驶时,悬索桥左跨跨中的竖向位移、速度和加速度,如图4所示。
车头车厢车体的竖向位移、速度和加速度,如图5所示。
图4、图5中横坐标表示列车第1节车厢外缘在桥上的位置,即第1节车厢外缘距左塔的距离。
当列车以速度100 km/h行驶时,悬索桥左跨跨中的最大竖向位移发生在列车位置的左边跨时,随着速度的增大,峰值发生位置逐渐后移,并且左跨跨中的竖向位移振荡明显增强,尤其是列车以速度300 km/h行驶时,振荡非常明显。
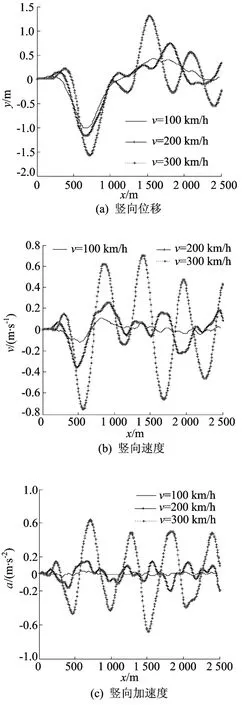
图4 悬索桥左边跨跨中的竖向位移、速度与加速度
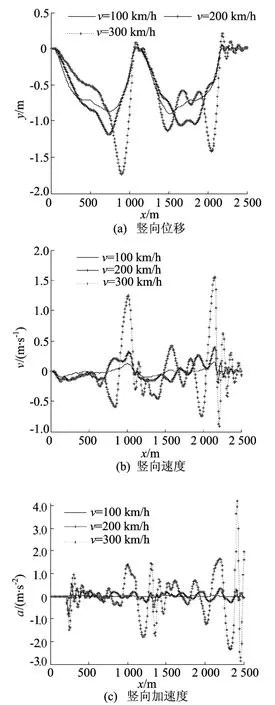
图5 列车车头车体的竖向位移、速度与加速度
5 结束语
本文推导了车桥耦合单元,建立了车桥耦合振动有限元法分析的状态空间法。对大跨度悬索桥在移动列车作用下的车桥耦合振动动力特性进行了研究。数值仿真结果表明本文方法具有很高的精度和计算效率。本文给出的方法计算程序简单,利用Ansys和M atlab软件可以分析复杂桥梁结构的车桥耦合振动问题。
[1] 逄焕平,王建国,李雪峰.基于挠度理论的悬索桥静力分析[J].合肥工业大学学报:自然科学版,2010,33(2):261-265.
[2] Chu K H,Garg V K.Railway-bridge impact:simplified train and b ridge model[J].Structural Engineering,1979,105(9):1823-1844.
[3] W ang T L,H uang D Z.Cable-stayed bridge vib ration due to road su rface roughness[J].Journal of Structu ral Engineering,1992,118(5):1354-1373.
[4] Guo X R,Zhen Q Y.Space vib ration analysis of the timedependent system of long span railw ay bridgesand train underw ind load[C]//Proceedings of W orkshop on Research and M onito ring of Long Span Bridges,Hong Kong,2000:40-45.
[5] Cheng Y S,Au F T K,Cheung Y K.V ib ration of railw ay b ridges under a moving train by using bridge-track-vehicle elemen t[J].Engineering Structu res,2001,23:1597-1606.[6] Yau JD,Yang Y B.Vib ration of a suspension b ridge installed w ith a w ater pipeline and subjected tomoving trains[J].Engineering Structu res,2008,30:632-642.
[7] Bruno D,Greco F,Lonetti P.Dynam ic impact analysis of long span cable-stayed bridgesundermoving loads[J].Engineering Structures,2008,30:1160-1177.
[8] Majka M,H artnett M.Dynam ic response of bridges to m oving trains:a study on effectsof random track irregu larities and b ridge skew ness[J].Compu ters and Structures,2009,87:1233-1252.
[9] Ding Lina,Hao H ong,Zhu Xinqun.Evaluation of dynamic vehic le axle loads on bridges with differen t su rface conditions[J].Jou rnal of Sound and V ib ration,2009,323:826-848.
[10] 逄焕平,大跨度悬索桥成桥状态的确定及其车桥耦合振动分析[D].合肥:合肥工业大学土木与水利工程学院,2010.
Analysis of vehicle-bridge interaction of long span suspension bridges
PANG Huan-ping1, WANG Jian-guo2, QIAN Feng2
(1.School of T ransportation Engineering,H efei University of Technology,H efei 230009,China;2.School of Civiland Hyd raulic Engineering,Hefei University of Technology,Hefei 230009,China)
Based on finite element method,the vehicle-bridge interaction(VBI)(the coup ling interaction between the vehicles and bridges)can be transformed to a linear time-variant system.The system is decomposed of a linear time-variantsystem and a linear time-invariant system.Using themodalmatrix of linear time-invariant system and state spacemethod,the state space equation of the vehicle-bridge coupling system is obtained.The VBIproblem ofasuspension bridge subjected to amoving vehicle isanalyzed by using the presented method.
vehicle-bridge interaction(VBI);linear time-variant system;suspension bridge
U441.3
A
1003-5060(2011)01-0114-05
10.3969/j.issn.1003-5060.2011.01.027
2010-01-20;
2010-05-20
土木工程防灾减灾安徽省工程技术研究中心资助项目(2007368);中央高校基本科研业务费专项资助项目(2010HGZY0010)
逄焕平(1981-),山东胶南人,博士,合肥工业大学讲师;
王建国(1954-),安徽怀宁人,博士,合肥工业大学教授,博士生导师.
(责任编辑 张淑艳)
