海表热通量反馈及海温变率

余斌,George J.BOER,Francis W.ZW IERS

(1.加拿大环境部气候研究所气候数据与分析研究室,加拿大多伦多;2.加拿大环境部气候研究所加拿大气候模拟与分析中心,加拿大维多利亚;3.维多利亚大学太平洋气候影响研究部,加拿大维多利亚)

0 引言

海气界面的能量交换与海洋平流一起控制海面温度(sea surface temperature,SST)异常的形成、维持和衰减。一般来说,海洋热输送支配赤道太平洋东部SST异常(Philander,1990),而月平均海表热通量(surface heat flux,SHF)异常与SST倾向在海洋的中高纬度地区显著相关(Cayan,1992)。热通量和SST之间的关系反映了SHF在大尺度SST异常的动力学过程中所扮演的复杂角色;热通量既有助于SST异常的产生,也作用于SST的演变及衰亡。在适当的假定下,SHF可以进一步分解为大气强迫项和热通量反馈项之和(Frankignoul,1985)。SST异常和SHF异常之间的关系通常与所用模式有关,有时还与SST异常的地理位置以及SST异常正负号有关(Kushnir and Lau,1992;Frankignoul et al.,1998)。

基于海表面能量收支平衡,我们将SST变率的大尺度特征与海表热通量以及海洋热输送变率联系起来(Yu and Boer,2003,2006)。此外,我们分析了NCEP/NCAR(美国国家环境预测中心/美国大气研究中心)再分析资料、ECMWF(欧洲中期天气预报中心)再分析资料以及CM IP3(第3阶段的全球耦合模式比较计划)多模式气候模拟存档资料中的SHF和SST之间的协方差特征(Yu et al.,2009)。分析SHF-SST同时协方差有助于我们认识SST异常的发展和抑制,而它们之间的滞后交叉协方差分析有助于认识SHF的反馈作用。因此,分析SHF-SST间的协方差关系可以帮助我们理解与SST变率相关的物理过程。

1 海表热通量反馈

1.1 SHF反馈

海洋上层能量收支异常可以写为

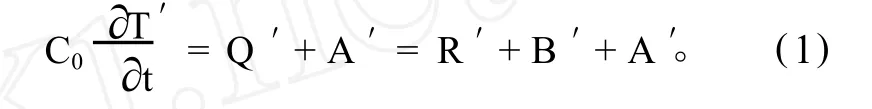
其中:C0表示海洋混合层上层热容量,近似为常数;T是SST;Q=R+B是净表面热通量,它包括辐射(R,太阳短波辐射和净红外辐射)和湍流(B,潜热和感热)表面能量交换;A是海洋热输送的散度。我们定义所有热通量向下为正,即热通量利于SST增强为正。上标撇号表示与气候平均值的偏差。

热通量异常Q′近似为一个大气强迫项(q′)以及一个与SST成正比的反馈项(-λQT′)之和,即

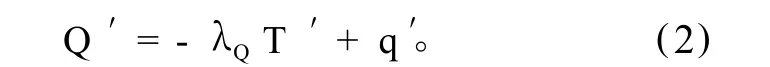
其中λQ是热通量反馈参数。参照Frankignoul et al.(1998)、Frankignoul and Kestenare(2002)的工作,热通量反馈参数由SST-SHF间的滞后交叉协方差)以及SST自协方差()决定。在热带外区域,q′代表了较小时间尺度的随机过程。假定大气强迫作用影响SST,但SST不直接反作用于强迫项,则其滞后协方差(τ)=0(τ＜0,T′超前q′)。这样,SHF的反馈参数可由以下方程估算

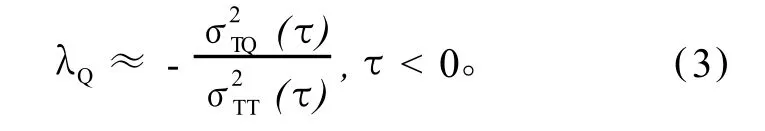
类似此前的研究(Frankignoul and Kestenare,2002;Yu and Boer,2006),SHF反馈参数通过滞后1～3个月的平均λQ结果而得。注意反馈参数的正值表示负反馈的强度,反之亦然。

由于大气的持续性影响不能直接从热通量中分离出来,所以在SHF反馈参数估算方程(3)中假设大气谱为低频白噪音。这种假定在热带外区域成立,除了需要在大气强迫项中扣除ENSO变化(最重要的一种年际变率)可能带来的低频分量。我们通过线性回归分析法消除了ENSO在SST和SHF中的影响。这里,ENSO引起的SST变化定义为12.5°S与12.5°N之间热带太平洋SST异常的前两个主分量之和。

1.2 再分析资料与耦合气候模拟中的SHF反馈

图1为利用两个再分析资料以及CM IP3多模式集合平均求得的净通量及其辐射和湍流分量的SHF反馈参数的地理分布(Yu et al.,2009)。分析结果基于NCEP/NCAR2再分析资料(NCEP2;Kanam itsu et al.,2002)、ERA-40再分析资料(Uppala et al.,2005)以及CM IP3中20C3M的气候模拟结果(M eehl et al.,2007)。为了方便分析,资料的时段均统一为1980年1月—1999年12月。由于存在强的海气相互作用,SHF反馈无法在热带太平洋地区得到可靠估算,故不在图中示出。强的净热通量负反馈(-λQT′),即正λQ值,出现在两半球中纬度地区,数值超出24W·m-2·K-1,最大值出现在大洋的中西部并向高纬度地区延伸(图1a、d、g)。在北大西洋副极地环流部分地区也有强的反馈。两个再分析结果有很好的对应关系,仅仅在数量上有微小差别,两者空间分布的相关系数为0.95。多模式集合平均SHF反馈参数比再分析结果偏弱,这也许与大气环流模式及再分析同化系统间不同的海气耦合过程对海表热通量阻尼效应有关(Barsugli and Battisti,1998;Saravanan,1998;W u et al.,2006)。然而,反馈参数空间分布与再分析资料匹配很好,模式结果与两种再分析结果之间相关为0.95。湍流热通量反馈(λB,图1c、f、i)决定净通量反馈。辐射反馈(λR,图1b、e、h)基本为弱的负值,除了很少一些地区出现弱的正反馈。

图2为模式间SHF反馈参数的标准差;图3为比较反馈参数空间形态以及方差比的BL T统计图。它们用于评估CM IP3中20个气候模式与两种再分析结果间的相对相似程度。BLT图是一个改进的Taylor图(Boer and Lam bert,2001),它显示了与NCEP2及ERA-40平均值相比的各气候模式的空间形态相关性、相对均方差以及方差比率。

模式间的净SHF反馈参数的标准差与多模式集合平均相似,最大值主要出现在湾流区并向更高纬度地区延伸至副极地环流部分区域(图2a)。同时,模式间的标准差小于多模式集合平均,表明各模式具有整体一致性,但在SHF反馈高值区与海冰边缘区差异最明显。与之相反,海表面辐射反馈参数的模式间的标准差与多模式集合平均值相当,尤其是在热带大西洋和湾流地区,表明辐射通量反馈在各模式中差异很大,甚至会改变这些区域的平均辐射负反馈特性。

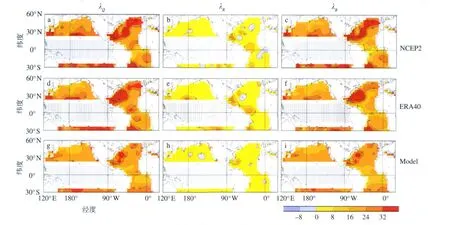
图1 NCEP2(a,b,c)、ERA-40(d,e,f)和多模式集合平均(g,h,i)的净(a,d,g)、辐射(b,e,h)和湍流(c,f,i)热通量反馈参数(等值线间隔为8W·m-2·K-1;竖线范围表示受ENSO影响而无法较好推算反馈参数区域;图引自Yu et al.(2009))Fig.1 (a,d,g)Net,(b,e,h)radiative and(c,f,i)turbulent surface heat flux feedback parameters for(a,b,c)NCEP2,(d,e,f)ERA-40,and(g,h,i)the multi-model mean(Contour interval is8W·m-2·K-1.The vertically hatched areas indicate that the feedback parameters are not estimated because of the effects of ENSO-related low frequency variability.Panels from Yu et al.(2009))

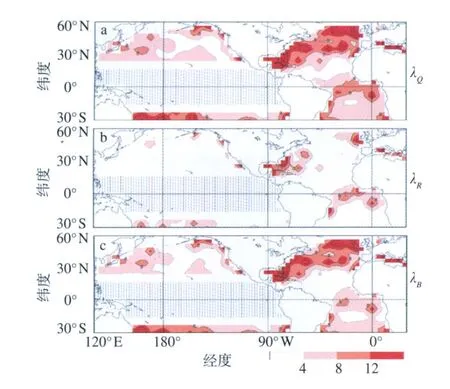
图2 净(a)、辐射(b)和湍流(c)热通量反馈参数(λQ,λR和λB)的模式间的标准差(等值线间隔为4 W·m-2·K-1;竖线范围表示受ENSO影响而无法较好推算反馈参数区域;图引自Yu et al.(2009))Fig.2 Inter-model standard deviations of(a)the net,(b)radiative and(c)turbulent heat flux feedback parameters(λQ,λR,andλB)(Contour interval is4 W·m-2·K-1.The vertically hatched areas indicate that the feedback parameters are not estimated because of the effects of ENSO-related low frequency variability.Panels from Yu et al.(2009))

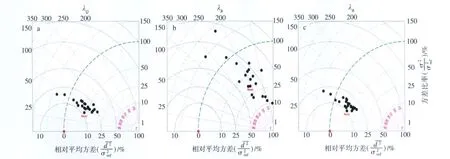
图3 BLT图表征模式及再分析结果的相对平均方差和方差比率,以及模式与再分析结果的空间形态相关性(再分析结果是NCEP2和ERA-40的平均;平均模式结果也在图中给出;图引自Yu et al.(2009)) a.λQ;b.λR;c.λBFig.3 BLT diagrams illustrating the relative mean square difference,the ratio of the modeled to reanalyzed variance,and the pattern correlation between model and reanalysis components(The reanalyzed components are the means of NCEP2 and ERA-40.The mean model result is also shown.Panels from Yu et al.(2009)) a.λQ;b.λR;c.λB

图3为净、辐射和湍流热通量的反馈参数BL T图。就空间形态而言,λQ在所有模式和再分析结果间的对应相关系数均很高(图3a)。多模式集合平均与再分析结果平均的相关系数为0.96,表明多模式集合平均与再分析结果平均享有约92%一致的空间方差。多模式平均和再分析平均λQ的相关比任何单一模式与再分析平均的相关(范围为0.89～0.95)都高。从这个角度来衡量,平均模式整体来说是最好的模式。然而,模式和再分析反馈参数的方差比率显示,多模式平均λQ(图1)的空间方差仍比再分析的估值低。湍流通量统计结果(图3c)类似于净通量统计结果。相比之下,模式λR统计值与再分析值吻合度不高(图3b),尽管这是一个较小的反馈参数。

1.3 反馈的季节性特征

SHF反馈的空间分布在4个标准季节的结果(图略,参阅Yu et al.,2009)与使用所有月份资料获取的结果(图1)相似。反馈参数在冬季(DJF)和秋季(SON)加强,表明在这两个季节里热通量对SST有较强的负作用;反馈参数在春季(MAM)和夏季(JJA)减弱。这种季节差异也许与冬季(DJF)和秋季(SON)相对较大的地面风速变化有关(例如:Frankignoul and Kestenare,2002)。反馈的季节变化特征在多模式集合平均以及单模式中均得到较好体现。然而,与再分析结果比,模式的反馈参数值总体上被低估了,尤其在北半球秋、冬季。

2 SST方差与热通量、热输送方差之间的关系

2.1 总体关系

基于海表能量收支方程(1),Yu and B oer(2006)将SST方差与海表热通量、海洋热输送方差之间的关系表述为

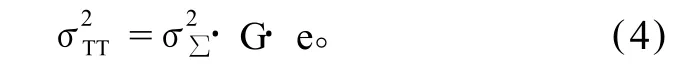
方程(4)中每一项都代表了能量收支的一个方面。与SST方差()相联系的有:与时间尺度有关的传输系数G;热通量、热输送方差;与协方差结构有关的因子e。衡量能量收支中热通量、热输送项的总体方差效应。若海表热通量及海洋热输送之间不存在关联,则热通量、热输送将维持SST方差变率。G取决于SST时间序列的自相关结构以及有效混合层的热容量。e表征各物理强迫机制之间相互抵消特性。注意e=1表示线性无关的过程(所有相关系数r=0)。相同的关系式适用于不同时间尺度,但传输系数G不相同。

2.2 波谱描述

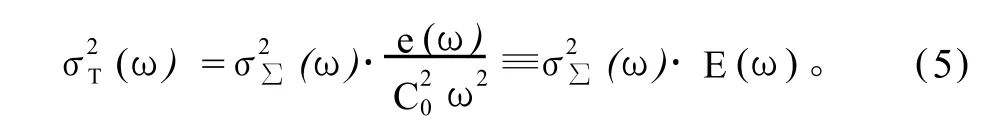
对方程(1)作傅立叶变换,SST方差与热通量、热输送方差之间的波谱关系可表述为其中:(ω)=(ω)+(ω)+(ω),表示如果热通量、热输送间不存在线性相关,则它将决定SST变率;e(ω)=1+2(σRσBCcoh-RBcosφRB+σRσACcoh-RAcosφRA+σBσACcoh-BAcosφBA)/(ω),取决于各强迫项之间在时间上的协变;ω是频率;Ccoh-xy是相关协谱;φxy是相位谱(例如:von Storch and Zw iers,1999);E(ω)(Yu and Boer,2003)。

图5显示了在太平洋(150°E～120°W)区域纬向平均统计方差结果。各格点上3次拟合趋势以及年循环在计算谱结果前都已从月度资料中扣除。结果基于1949年1月到1998年12月的50a NCEP1再分析数据(Kistler et al.,2001)。纬向平均SST方差主要反映了不同纬度上年际和年代际方差特征。在年际时间尺度上,沿赤道最大值集中于2～7a,与ENSO方差变化有关。在年代际时间尺度上,SST谱在热带和中纬度都存在大值。特征与SST方差特征相似,只是其热带中心在经向伸展更宽,强度在中纬度较弱。在热带,海洋热输送(ω)在年际时间上支配了(ω),而(ω)和(ω)对于年代际SST方差的贡献相当。在中纬度,A和B的方差贡献在两种时间尺度上均同等重要(图略)。海表辐射和湍流通量以及海洋热输送的方差之和被它们之间的协方差负贡献所抵消,SST方差为这两种相反作用所平衡。E(ω)直接联系着SST方差与热通量、热输送方差。

3 结论

SST与SHF之间的二阶统计量、方差和协方差描述了SST变率和SHF反馈的物理特性。本文回顾了SHF反馈以及SST方差与热通量、热输送方差之间的关系。

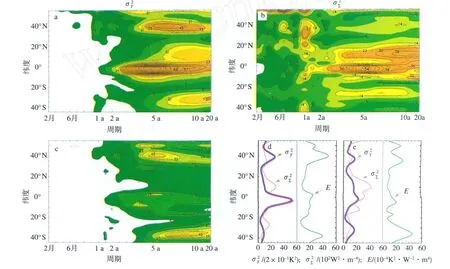
图5 基于1949年1月—1998年12月NCEP1再分析资料的纬向(150°E～120°W)平均SST谱值(a;单位:10-1K2)、热通量和热输送方差谱(b;单位:102W2·m-4)、因子E(c;单位:10-4K2/(W2·m-4))以及它们在5a(d)和15a(e)的结果(图5d-e中,SST谱密度的单位为2×10-1K2,通量谱密度的单位为102W2·m-4,因子E的单位为10-4K2/(W2·m-4))Fig.5 Zonally(150°E—120°W)averaged(a)temperature spectra(10-1K2),(b)the sum of heat flux/transport spectra(102W2·m-4),(c)the factor E(10-4K2/(W2·m-4)),and their values at(d)5-yr and(e)15-yr based on the NCEP1reanalysis from January1949to December1998(In Fig.5d-e,units of2×10-1K2for temperature power spectral density,102W2·m-4for flux power spectral density,and10-4K2/(W2·m-4)for E)

依据Frankignoul and Kestenare(2002)所提的方法,SHF反馈参数可由SST-SHF交叉协方差和SST自协方差估算。热通量反馈主要由与其湍流分量相关的负反馈所决定。强的负反馈位于南北两半球的中纬度地区,最大值出现在太平洋和大西洋的中西部海域,并伸展到高纬度地区。负的湍流和净热通量反馈在北半球秋、冬季较强,春、夏季较弱。年和季节反馈特征在CM IP3多模式集合平均以及各模式中均得到较好模拟。与再分析结果比,在所有模式中,平均模式拥有最好的空间形态相关性,并且均方差最小,尽管其量值仍比再分析结果偏低。

SST的方差可以表示为3个要素之积:1)海表辐射和湍流通量以及海洋热输送的方差之和;2)一个表征SST持续性的传输系数G;3)反映海表热通量及海洋热输送之间协方差结构的一个有效因子e。SST方差的地理分布与海表热通量及海洋热输送的方差之和相类似,但为G和e因子所修正。这种现象在季至年代际的时间尺度上均可见。

致谢:余斌为曾就读于南京气象学院,并能在朱乾根教授的指导下取得硕士学位感到荣幸。朱先生是将余斌引入研究生涯的最重要的导师之一。他的科学洞察力以及正直、热情和耐心使余斌深受鼓励。同时,余斌也感激朱先生与师母李教授在我学习期间给予的生活上的关心和学业上的指导。作者也感谢两位匿名审稿专家对该研究所提供的有益评论和建议。本文为纪念朱乾根教授而作。感谢智协飞教授对稿件的关心以及赵文焕、倪东鸿编审对译稿所付出的努力。

Barsugli J J,Battisti D S.1998.The basic effects of atmosphere-ocean thermal coupling on midlatitude variability[J].J A tmos Sci,55:477-493.

Boer G J,Lambert S.2001.Second-order space-time climate difference statistics[J].Clim Dyn,17:213-218.

Cayan D R.1992.Latent and sensible heat flux anomalies over the northern oceans:D riving the sea surface temperature[J].J Phys Oceanogr,22:859-881.

Frankignoul C.1985.Sea surface temperature anomalies,planetary waves and air-sea feedback in the middle latitudes[J].Rev Geophys,23:357-390.

Frankignoul C,Czaja A,HevederB.1998.A ir-sea feedback in the North Atlantic and surface boundary conditions for ocean models[J].J Climate,11:2310-2324.

Frankignoul C,Kestenare E.2002.The surface heat flux feedback.Part I:Estimates from observations in the Atlantic and the North Pacific[J].Clim Dyn,19:633-647.

Kanamitsu M,EbisuzakiW,W oollen J,et al.2002.NCEP-DOE AMIPII Reanalysis(R-2)[J].Bull Amer Meteor Soc,83:1631-1643.

Kistler R,Kalnay E,Collins W,et al.2001.The NCEP-NCAR50-year reanalysis:Monthly means CD-ROM and documentation[J].Bull Amer Meteor Soc,82(2):247-268.

Kushnir Y,Lau N C.1992.The general circulation model response to a North Pacific SST anomaly:Dependence on time scale and pattern polarity[J].J Climate,5:271-283.

Meehl G A,Covey C,Del worth T,et al.2007.The WCRP CMIP3 multi model dataset:A new era in climate change research[J].Bull A-mer Meteor Soc,88:1383-1394.

Philander S G H.1990.El N i~no,La N i~na and the Southern Oscillation[M].San Diego:Academic Press.

Saravanan R.1998.Atmospheric low-frequency variability and its relationship to midlatitude SST variability:Studies using the NCAR climate system model[J].J Climate,11:1386-1404.

Uppala S M,KÅllberg P W,Simmons A J,et al.2005.The ERA-40reanalysis[J].Quart J Roy Meteor Soc,131:2961-3012.

von Storch H,Zwiers F.1999.Statistical analysis in climate research[M].Cambridge:Cambridge University Press.

Wu R,Kirtman B P,Pegion K.2006.Local air-sea relationship in observations and model simulations[J].J Climate,19:4914-4932.

YuB,Boer G J.2003.Spectral relationships between surface temperature and heat fluxvariability[C]∥Procofthe18th Stanstead Seminar,Québec.

Yu B,Boer G J.2006.The variance of sea surface temperature and projected changes with global warming[J].Clim Dyn,26:801-821.

Yu B,Boer G J,Zw iers F,et al.2009.Covaria bility of SST and surface heat fluxes in reanalyses and CMIP3climate models[J].Clim Dyn,doi:10.1007/s00382-009-0669-6.