一类Z-tile成为a，1-框架集的充要条件

刘春苔

(武汉工业学院数学与计算机学院，湖北武汉，430023)

设H是一个可分Hilbert空间，{ fn}n∈Z是其上的一个可数集族.如果存在正常数A，B，使得对于任意f∈H，有

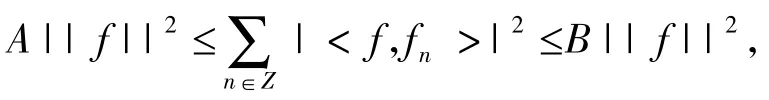
则称{fn}为H的一个框架，且称A为框架下界，B为框架上界.

在L2(R)上定义算子Ta，Eb为

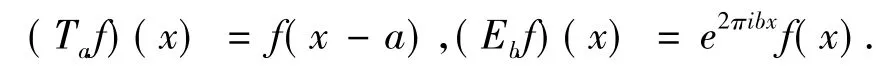
对于任意 g ∈ L2(R)，称{e2πimbxg(x-na)}m，n∈Z={EmbTnag}m，n∈Z：=(g，a，b) 为一个 Gabor系统，此时称g为一个窗口函数.如果(g，a，b)为一个框架，则称(g，a，b)为一个Gabor框架，也称为Weyl-Heisenberg框架(WH框架).

在应用中，平方可积空间中的WH框架往往为人们所关注［1-5］.很自然地有，

问题：在L2(R)中，Gabor系统(g，a，b)何时成为一个WH框架?

这个问题相当复杂，目前只解决了某些特殊情形(详见文献［1］).鉴于一般窗口函数，WH框架的存在性很难刻画，所以一个有效的处理方法是将窗口函数限制为一个简单函数甚至限制为可测集E的特征函数 χE(x)，若 Gabor系统(χE，a，b)为 WH框架，则称此可测集E为a，b框架集.有大量文献涉及到框架集的存在性，比如Gu和Han［6］系统的讨论了WH框架的a，b，c问题，方法是对实直线进行分类，然后计算框架的上、下界.Han和Wang［7］讨论了高维空间上的网tile成为WH框架集，此时平移调制参数被替换为满秩矩阵.Janssen［8］利用Zak变换将判别Gabor系统是否为WH框架转化为判别一个共轭对称阵是否为正定阵.值得指出的是，何［9］证明了若则(g，a，1)为WH框架的充分且必要的条件是 h在单位圆上没有根，此处序列{ an}满足这推广了Casazza和Kalton［4］的结果：将WH框架集的存在性转换为多项式的零点分布问题.

本文主要考虑两个区间并所构成的Z-tile可测集E成为a，1-框架集的条件，主要思想来源于文献［10］，得到如下定理，这里记号［x］表示不超过x的最大整数.

定理1设集E为两个区间的不交并，0＜a＜1.若E为Z-tile，则存在n∈Z，c∈R，0 ＜ r＜1使得 E= ［0，r)∪［n+r，n+1)+c.此时集 E 为a，1-框架集等价于下面两条之一成立：

(1)a ≤max{r，1-r};

(2)n-［n/a］a∈ {0}∪ {2a-1，a}.

1 若干记号和引理

首先给出若干记号，细节请参见文献［10］.设c＞0，R上可测集E具有有限正Lebesgue测度，即0＜μ(E)＜∞.定义R到N∪{∞}上的函数τc为

τc(x)=#{y∈E：存在某个整数 j使得y=x+cj}，这里#E表示集E的势.记E(c，k)={x∈E：

τc(x)=k}，k∈N∪{∞}.记号E+F表示E+F={e+f：e∈E，f∈F}.称集E为R的一个c覆盖，如果

进一步，如果上述并是不交的(在Lebesgue测度意义下，下同)，则称E是一个c-tile.当c=1时，称集E为一个Z-tile.

引理1［10］设正实数a，b满足ab≤1，集E满足0＜μ(E)＜∞.如果集E满足(1)E(1/b，1)是R的一个a-覆盖;(2)存在某个k使得对任意l≥k有E(1/b，l)=E(a，l)= Ø，则E为一个a，b-框架集.

引理2［10］设E⊂R，j∈Z，k1，k2∈N∪{∞}，且 k1≠ k2.则 E(c，k1) ∩ (E(c，k2+cj)= Ø.且

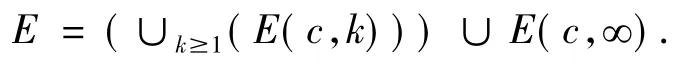
进一步，若μ(E) ＜+∞，则E(c，+∞)=Ø.

引理3设集E是两个区间的不交并.若E是一个Z-tile，则存在整数n和实数c，r，使得E具有如下形式 E= ［0，r］∪［n+r，n+1］+c，其中r满足0＜r＜1.

证明：设 E= ［a1，a2) ∪［a3，a4)：=E1∪E2+a1，其中 E1= ［0，a2-a1)，E2= ［a3-a1，a4-a1)，且a1＜a2＜a3＜a4.因为E是Z-tlie，所以

R= ∪n∈Z(E+n) =∪n∈Z(E1∪ E2+n) =(∪n∈Z(E1+n)) ∪ (∪m∈ZE2+m)

注意到上式右端并是不交的，从而a2-a1＜1，且存在整数m使得，［0，1］=E1∪(E2+m)，所以E2+m= ［a2-a1，1)，令r=a2-a1，n=-m，c=a1，则 E可表为

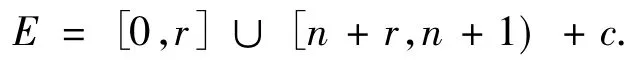
引理4设集E是两个区间的不交并且集E是一个Z-tile，则 (1)E(1，1)=E;(2)对于任意实数a＞0，存在正整数k=k(a)，使得E(a，l)=Ø，l≥ k.

证明：因为μ(E)＜+∞，故由引理3知，对于任意正数c，E(c，∞)=Ø.从而

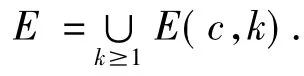
再由引理3 可知，E= ［0，r］∪［n+r，n+1］+c，其中0 ＜r＜1.

(1)注意到对任意x∈R，存在唯一的一对数(y，n)∈E ×Z使得x=y+n，所以τ1(x)=1，于是 τ1(E)={1}，从而 E=E(1，1).

(2) 取k=［(n+1)/a］+1，则ka＞n+1.所以E-c⊂［0，ka)，因此对任意实数x，有τa(x) ＜k，从而τa(E)⊂{1，2，3，…，k-1}，于是当l≥k时有 E(a，l)= Ø

推论：设 E= ［0，r)∪［n+r，n+1)+c，0＜r＜1，0＜a≤1.则存在正整数k，使得当l≥k时有 E(1，l)=E(a，l)= Ø.

2 定理1的证明

引理5设 E= ［0，r) ∪［n+r，n+1)，1/2≤r＜1.r＜a＜1.若n-［n/a］a≥2a-1或者n/a为整数，则E是R的一个a覆盖.

证明：注意到

其中整数m满足n≤ma≤n+r.

(1)当n/a∈Z时，有n/a=m.因为

［0，r) ∪［n+r-ma，n+1-ma)= ［0，1) ⊃［0，a)

所以集E是R的一个a覆盖.

(2)而当n/a∉Z时，设l=［n/a］，a1=nla.此时由m的定义知m=l+1.显然

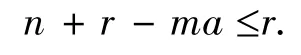
再由题设条件a1≥2a-1知

n+1-ma=la+a1+1-(l+1)a=a1+1-a≥ a.

因此由(1)式知集E是R的一个a覆盖.

定理1的证明：集E的表达式E=［0，r)∪［n+r，n+1)+c已由引理4得到，下面只需刻画集E成为a，1-框架集的充要条件.由推论6和引理2知集E是一个a，1-框架集当且仅当集E是R的一个a覆盖.由于对称性，不妨设1/2≤r＜1.

充分性.当a≤r时，集E显然是R的一个a覆盖.当r＜a＜1时.只需考虑c=0的情形，即E=［0，r)∪［n+r，n+1).而在这种情形下，引理7已证集E是R的一个a覆盖，故集E是一个a，1-框架集.

必要性.由充分性知，只需验证当a＞r且0＜a1＜2a-1时，集E不是R的一个a覆盖即可.令l= ［n/a］，则

n+r-(l+1)a＜a1-a+r＜r，n+1-(l+1)a=a1+1-a ＜ a，

所以(a1+1-a，a) ⊄∪k∈Z(E+ka)，即证集E不是a，1-框架集.

［1］ Casazza P G.The art of frame theory［J］.Taiwanese J Math，2000，5(2)：129-201.

［2］ Casazza P G.Modern tools for Weyl-Heisenberg(Gabor)frame theory［J］.Adv Imag Elect Phys，2001，115：1-127.

［3］ Casazza P G，Christensen O.Weyl-Heisenberg frames for subspaces of L2(R) ［J］.Proc Amer Math Soc，2001，129：145–154.

［4］ Casazza P G.Kalton N J.Roots of complex polynomials and Weyl-Heisenberg frame sets［J］.Proc Amer Math Soc，2002，130(8)：2313-2318.

［5］ Casazza P G，Christensen O.Gabor frames over irregular lattices［J］.Adv Comput Math，2003，18(2-4)：329-344.

［6］ Gu Q，Han D G.When a characteristic function generates a Gabor frame［J］.Appl Comput Harmon Anal，2008，24(3)：290-309.

［7］ Han D G，Wang Y.The existence of Gabor bases and frames［J］.Wavelets，frames and operator theory，2004，345：183-192.

［8］ Janssen A J E M.Zak transforms with few zeros and the tie［C］.Advances in Gabor analysis，31-70，Appl Numer Harmon Anal，Birkhauser Boston，Boston，MA，2003.

［9］ He X G，Lau K S.On the Weyl–Heisenberg frames generated by simplefunctions［J］.J Func Anal，2011，261：1010-1027.

［10］ Lian Q F，Li Y Z.Gabor frame sets for subspaces［J］.Adv Comput Math，2011，34：391-411.