基于平面参数法的道岔线型设计研究

2011-01-15曹洋王平赵卫华

铁道建筑 2011年2期

关键词：线型道岔侧向

曹洋，王平，赵卫华

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

基于平面参数法的道岔线型设计研究

曹洋，王平，赵卫华

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

随着高速铁路的发展，新建客运专线最高运行速度已达到350 km/h，道岔平面线型是影响列车过岔速度的关键因素之一。针对不同的过岔速度选择合适的道岔线型，计算后得到设计参数，对指导道岔选型和设计是十分必要的。利用平面参数法推导各种平面线型的计算公式，提出道岔线型设计流程，并通过实际算例比较了各种线型的应用范围及优劣性。研究表明，列车低速过岔时宜采用小号码单圆或复圆曲线道岔，高速情况下则宜采用含有缓和曲线的道岔线型;缓和曲线的加入，可以在减小圆曲线半径的基础上提高列车的侧向过岔速度，并满足平稳性要求。

平面参数法道岔线型设计流程应用范围缓和曲线

道岔是机车车辆从一股轨道转入或越过另一股轨道时必不可少的线路设备，是铁路轨道的一个重要组成部分。由于道岔具有数量多、构造复杂、使用寿命短、行车安全性低、养护维修投入大等特点，因此成为轨道结构的最薄弱环节，是限制列车行车速度的关键设备［1］。

随着高速铁路的发展，新建客运专线行车速度已超过200 km/h，最高速度可达350 km/h［2-3］，列车直向和侧向过岔尤其是通过高速大号码道岔时，其安全性、平稳性均要满足规定限值。道岔的平面线型是限制列车容许通过速度的重要因素，侧向高速道岔大多采用缓和曲线作导曲线［3-4］，因此高速大号码道岔的线型设计非常重要。本文利用平面参数法推导出各种线型道岔的计算公式，并通过平稳性分析提出不同侧向过岔速度下应选用的道岔号码及线型。

1 道岔线型设计

根据设计基本参数不同，道岔侧股曲线形式有单圆型、复圆型、圆缓型和缓圆缓型四种［5-7］。由于单圆型及复圆型道岔应用较为普遍，在此不再详述，而重点介绍带有缓和曲线的道岔平面线型的设计方法。

1.1 圆缓型道岔

圆缓型道岔单侧线型示意图如图1所示。

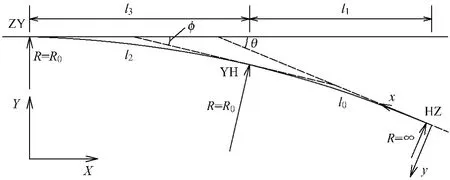
图1 圆缓型道岔单侧线型示意

其中θ为道岔辙叉角，即HZ点处切线与直股的夹角，φ为YH点处切线与直股夹角，R0为圆曲线半径，也即缓和曲线终点半径，整体坐标系下ZY点坐标为(Y0，0)，则YH点坐标为

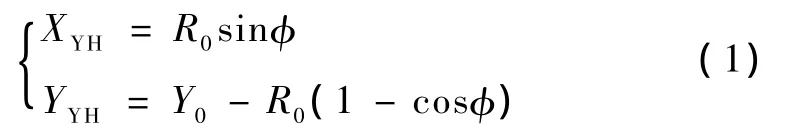
若缓和曲线长度为l0，在以HZ点为局部坐标系原点，切线方向为x轴，垂直x轴向下为y轴的局部坐标系中，对于YH点有

由式(1)、式(2)可得整体坐标系下HZ点坐标为

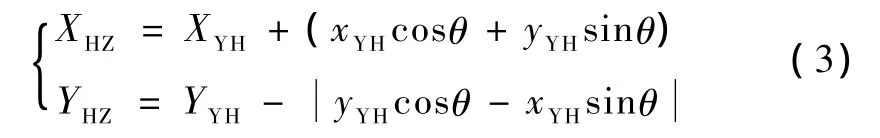
1.2 缓圆缓型道岔

缓圆缓型道岔单侧线型示意图如图2所示。

其中θ为道岔辙叉角，即HZ点处切线与直股的夹角，φ为YH点处切线与直股夹角，γ为HY点处切线与直股夹角，R0为圆曲线半径，也即两缓和曲线终点半径，R1为前缓和曲线起点半径。

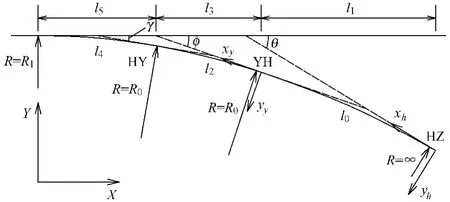
图2 缓圆缓型道岔单侧线型示意

若从前缓和曲线理论起点至实际起点长为lx，实际起点至HY点的长度为l4，则lx=l4R0/(R1－R0)，且两点间转角φ1=lx/(2R1)。以理论起点为局部坐标系原点，切线方向为x轴，垂直x轴向下为y轴，则局部坐标系下对于实际起点坐标(xQ，yQ)有

同样，对于HY点坐标有

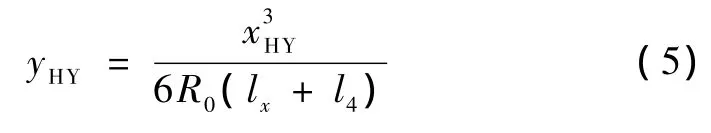
整体坐标系下前缓和曲线起点坐标为(Y0，0)，由式(4)、式(5)式得HY点坐标为

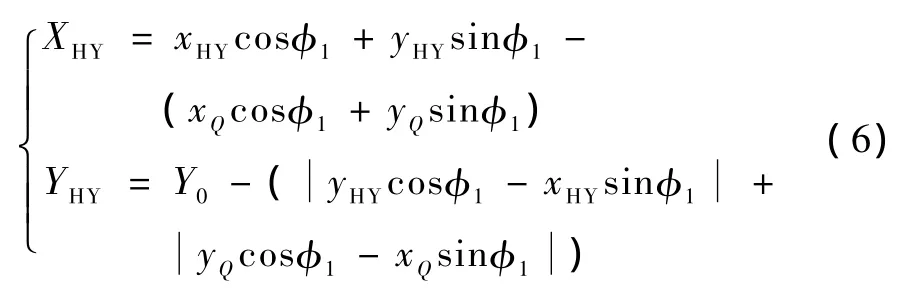
在以YH点为坐标原点，切线方向为x轴，垂直x轴向下为y轴的局部坐标系下，HY点坐标为

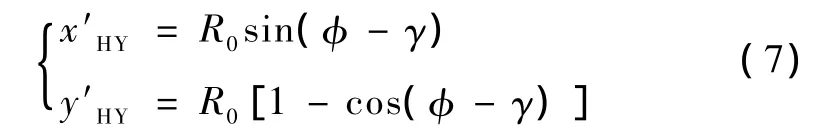
由式(6)、式(7)可得整体坐标系下YH点坐标为

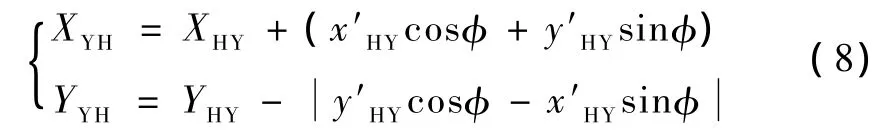
若后缓和曲线长度为l0，在以HZ点为局部坐标系原点，切线方向为x轴，垂直x轴向下为y轴的局部坐标系中，对于YH点坐标有

由式(8)、式(9)可得整体坐标系下HZ点坐标为

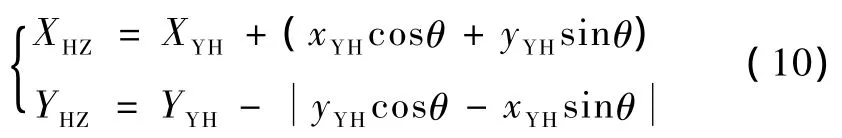
1.3 行车平稳性要求

为保证行车平稳性，曲线形式要满足未被平衡加速度及其时变率限值的要求，可根据列车位于道岔曲线不同部位分别计算［5-6］;同时要满足曲线长度大于列车振动周期内行进距离的要求，一般为列车开行0.8～1.0 s的距离;当两组道岔组成单渡线时，若为两圆曲线相接，为避免车辆通过曲线起终点产生的冲击振动与车辆的自振频率相吻合而发生振动迭加，需在两圆曲线间插入一定长度的夹直线［8］，其长度一般不小于车辆长度，且要大于(0.42～0.65)V(V为列车侧向过岔速度)。

2 线型设计流程

在道岔平面线型设计中，可根据道岔号码N是否已知进行具体研究。当N已知时，根据列车侧向过岔速度V，曲线半径R0等设计条件，在满足约束的情况下求出各曲线的特性值，从而绘制出平面线型图;若N未知，可通过假设曲线长度L，结合列车侧向过岔速度V，曲线半径R0等条件，得到道岔号码N，在选择合适的号码后，即可反推曲线长度，反复计算，直到满足设计要求为止。

3 算例分析

道岔平面线型设计主要影响列车侧向过岔的舒适性，以及由于曲尖轨的侧磨程度而影响其使用寿命的长短。列车侧向过岔速度分为三等，低速情况如80 km/h侧向进站，中速如160 km/h列车行驶于区间渡线道岔，侧向高速换线则为220 km/h。

当侧向过岔速度较低时，道岔线型一般采用单圆型曲线，有时为提高舒适性及减少尖轨侧磨，可采用道岔前端曲线半径较大的复圆型曲线。以24号道岔为例，不同工况下单圆型及复圆型道岔线型计算结果如表1所示。

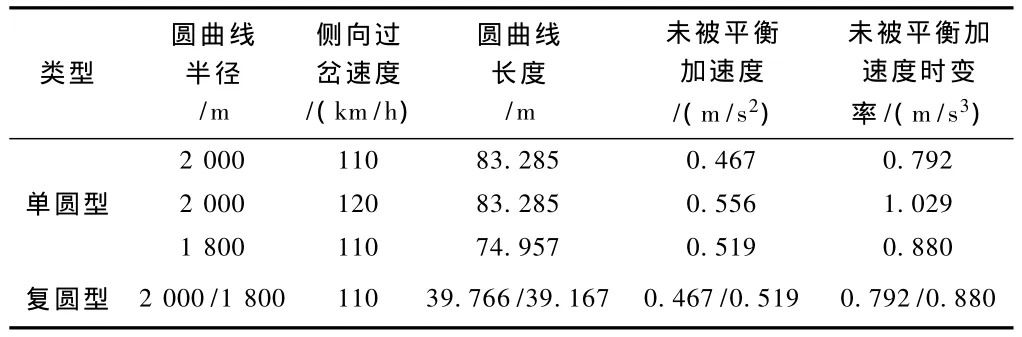
表1 圆曲线型道岔计算结果比较

由表1可知，列车以110 km/h侧向通过2 000 m半径的24号单圆型道岔时，车体未被平衡加速度及其时变率最大值分别为0.467 m/s2和0.792 m/s3，均小于客运专线道岔的设计限值0.5 m/s2和0.55～1.00 m/s3［9-10］;当侧向过岔速度为120 km/h时，车体未被平衡加速度及其时变率最大值分别为0.556 m/s2和1.029 m/s3，均超出设计限值;圆曲线半径减小为1 800 m时，虽然曲线长度有所减少，但车体未被平衡加速度达到0.519 m/s2，超出设计限值，此时若改为前端圆曲线半径为2 000 m的复圆型道岔，则尖轨处车体未被平衡加速度为0.467 m/s2，未超出限值，且曲线总长度比半径为2 000 m的单圆型曲线长度短。

当侧向过岔速度较高时，一般采用带有缓和曲线的道岔线型。以线间距4.6 m的38号道岔为例，缓圆缓线型的前缓和曲线起点半径取为10 000 m。不同工况下圆缓型及缓圆缓型道岔线型计算结果如表2所示。

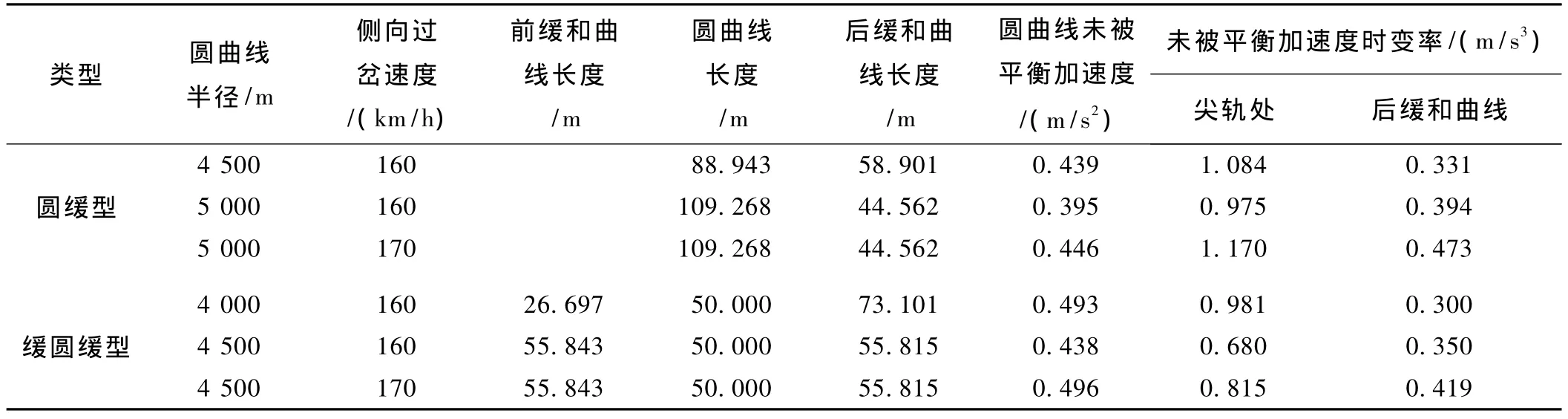
表2 缓和曲线型道岔计算结果比较

由表2可知，列车以160 km/h侧向通过38号圆缓型道岔，圆曲线半径取4 500 m时，尖轨处加速度时变率为1.084 m/s3，超出限值;当曲线半径为5 000 m时，圆曲线未被平衡加速度及尖轨处加速度时变率最大值分别为0.395 m/s2和0.975 m/s3，均未超限;若速度提高至170 km/h，则尖轨处加速度时变率为1.170 m/s3，超出限值，若速度继续提高，圆曲线未被平衡加速度也将超限，此时需加大圆曲线半径。

若采用缓圆缓型道岔，圆曲线半径为4 000 m，列车以160 km/h侧向通过时，圆曲线未被平衡加速度及尖轨处加速度时变率最大值分别为0.493 m/s2和0.981 m/s3，均未超限，但前缓和曲线长度较小，不易满足曲线最小长度的要求;增加圆曲线半径至4 500 m，当列车以170 km/h侧向通过时，圆曲线未被平衡加速度及尖轨处加速度时变率最大值分别为0.496 m/s2和0.815 m/s3，均未超限。