具Holling II功能反应的捕食系统的稳定性与最优收获策略问题

丁建华，雒志学，朱清泉

(兰州交通大学数理与软件工程学院，甘肃兰州 730070)

具Holling II功能反应的捕食系统的稳定性与最优收获策略问题

丁建华，雒志学，朱清泉

(兰州交通大学数理与软件工程学院，甘肃兰州 730070)

运用微分方程理论对具有Holling II功能反应的捕食系统进行研究.在适当的假设条件下，采用Routh-Hurwitz判别法证明了系统正平衡点是局部渐进稳定的，通过构造Liapunov函数证明了系统正平衡点是全局渐进稳定的，同时应用Pantryagin’s最大值原理给出了资源种群可持续生存的最优收获策略.

捕食系统；Holling II功能反应；正平衡点；稳定性；最优收获策略

早在1965年，Holling[1]在试验的基础上，对不同类型的物种，提出了3种不同的功能反应函数（Holling I、Holling II和Holling III）.此后，许多学者对具有Holling功能反应的捕食系统模型和多种群模型进行了广泛研究，得到许多深刻而系统的结论[2-8].2007年，Shiguan Ruan[9]等人构造了如下模型：

通过稳定性分析，得到了系统内部平衡点全局稳定的结论.本文对该模型进行了改进，对食饵种群x和捕食者种群z进行捕获，从而得到更加符合实际的模型.本文研究的数学模型如下：

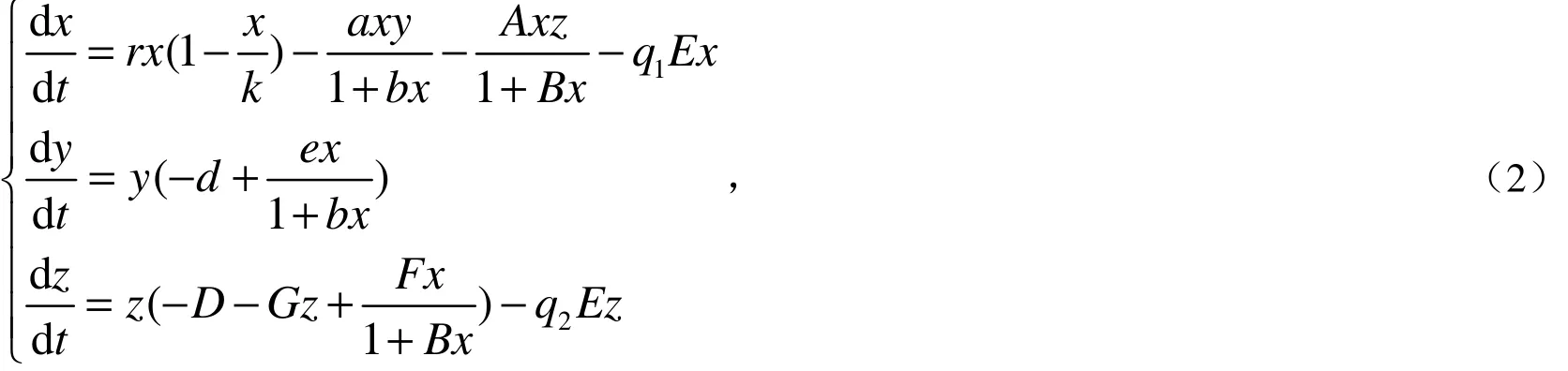
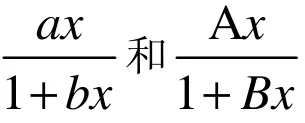
1 系统的有界性

定理1 系统（2）的所有解在R上是有界的.

2 正平衡点的存在性和稳定性

2.1 正平衡点的存在性

对于系统（2），经过计算可知，若满足条件

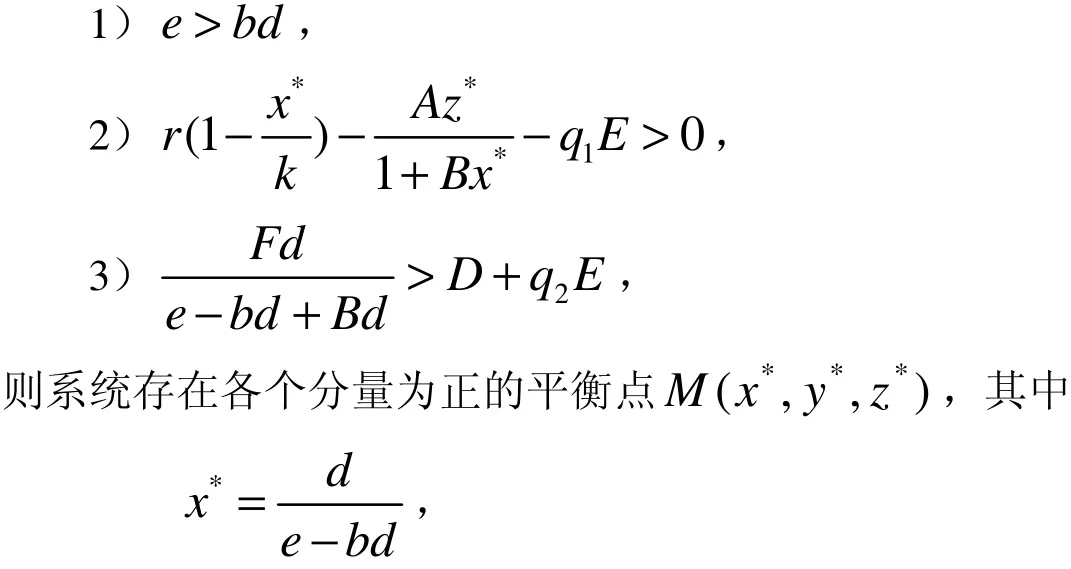
2.2 正平衡点的稳定性

定义函数

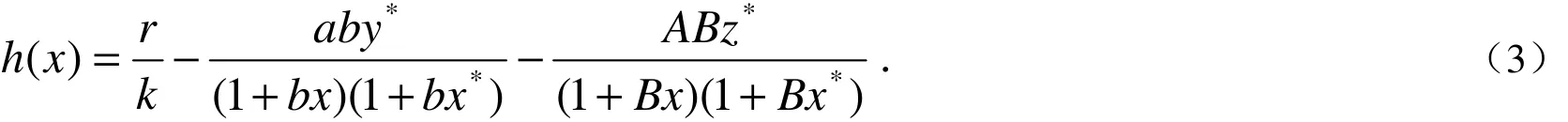
定理2 设正平衡点M存在.若x*h(x*) +Gz*> 0且h(x*)>h+*，其中

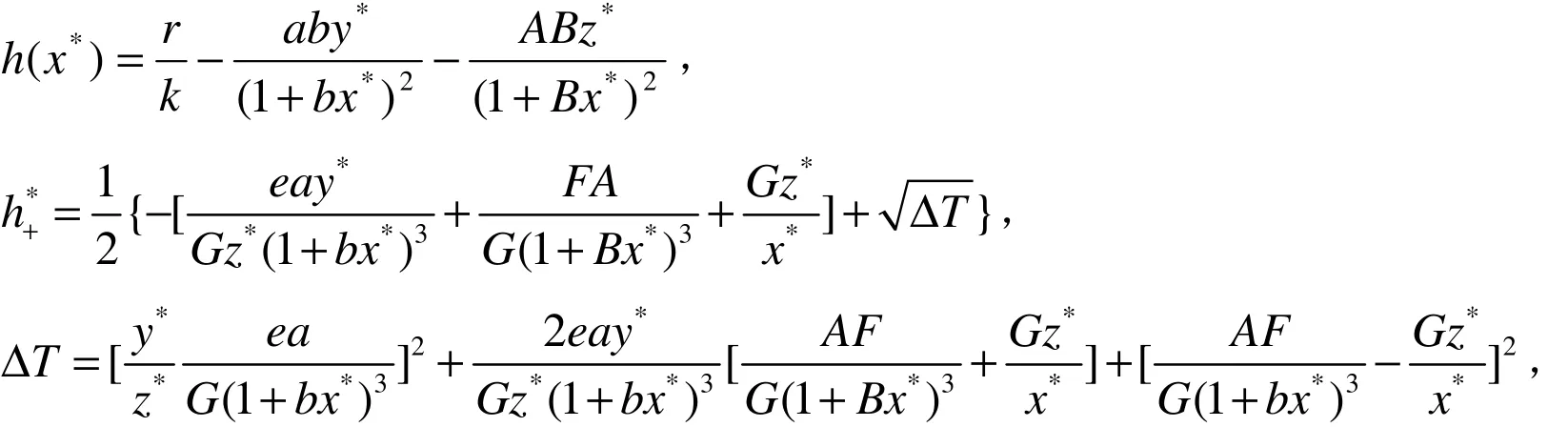
则它是局部渐进稳定的.

证明：系统（2）在正平衡点M(x*,y*,z*)处的雅可比矩阵为：

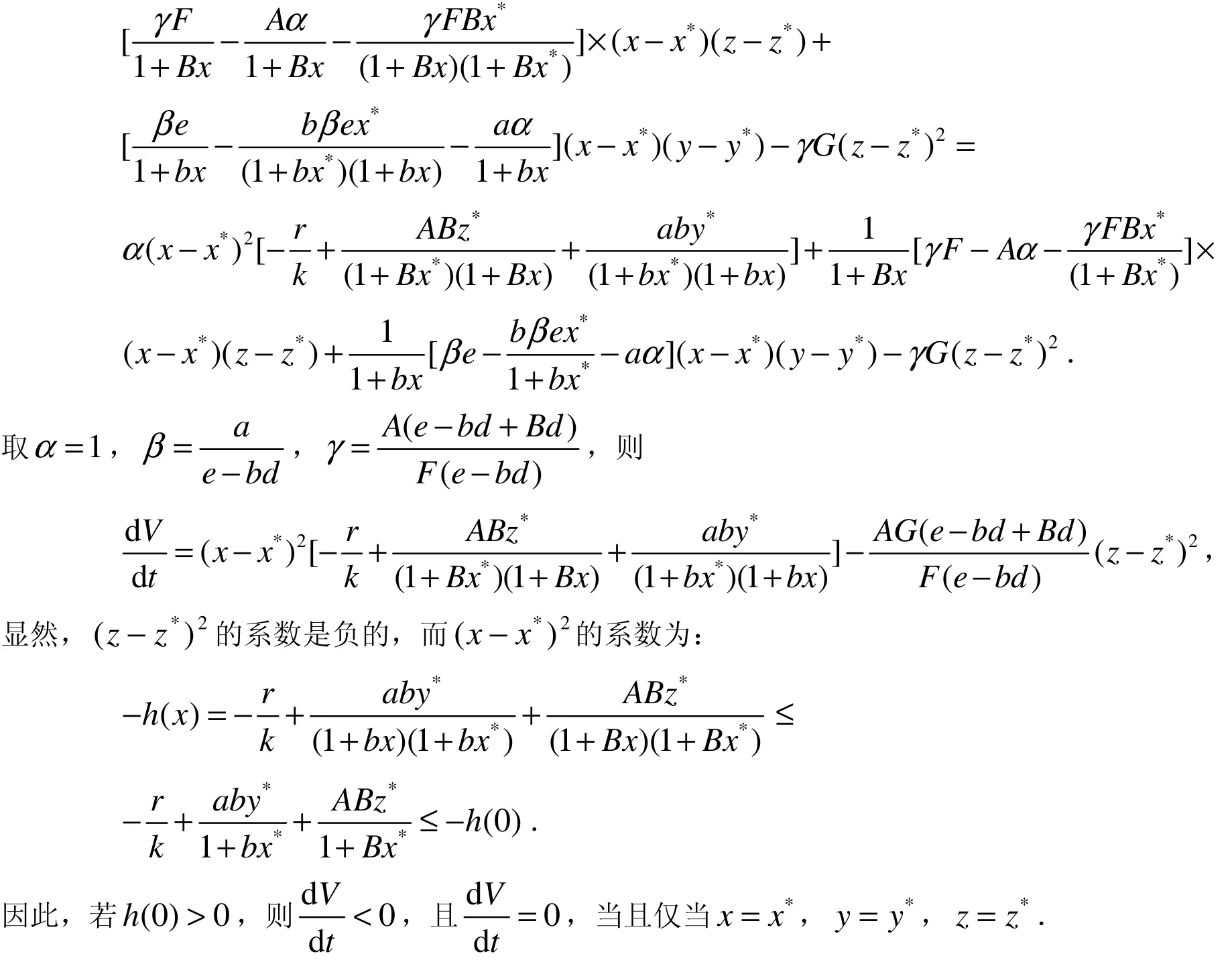
3 最优捕获策略

在这一部分，本文应用动态系统最优控制理论讨论如何控制捕获努力度E，才能使在长期开发中所获得的持续收益最大.假定种群x和z的单位市场销售价格和单位努力量的捕获成本恒定，分别为p1,p2,c，那么捕获主体开发种群资源的经营目标就是应用Pantryagin最大值原理[10]寻找一个最优的捕获努力量，使在长期资源开发中得到的贴现值

达到最大值，其中δ为贴现率，e−δt为贴现因子.

首先构建哈密顿函数：

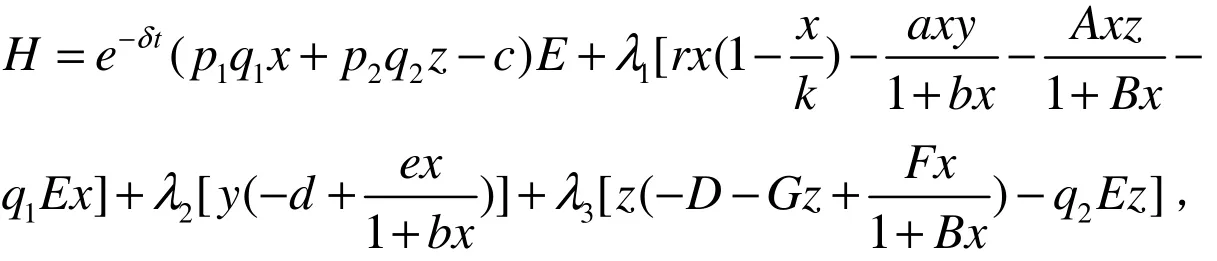
其中，λ(t),λ(t),λ(t)为伴随变量，u(t)=e−δt(pqx+pqz−c)−λqx−λqz为开关函

12311221132数.u(t) ≠0时的情况称为正常，此时的控制对应于Bang-Bang控制；u(t) = 0的情况称为奇异，此时的控制称为奇异控制.所以上述线性问题的最优控制必是奇异控制和线性控制的结合，即最优捕获有如下形式：

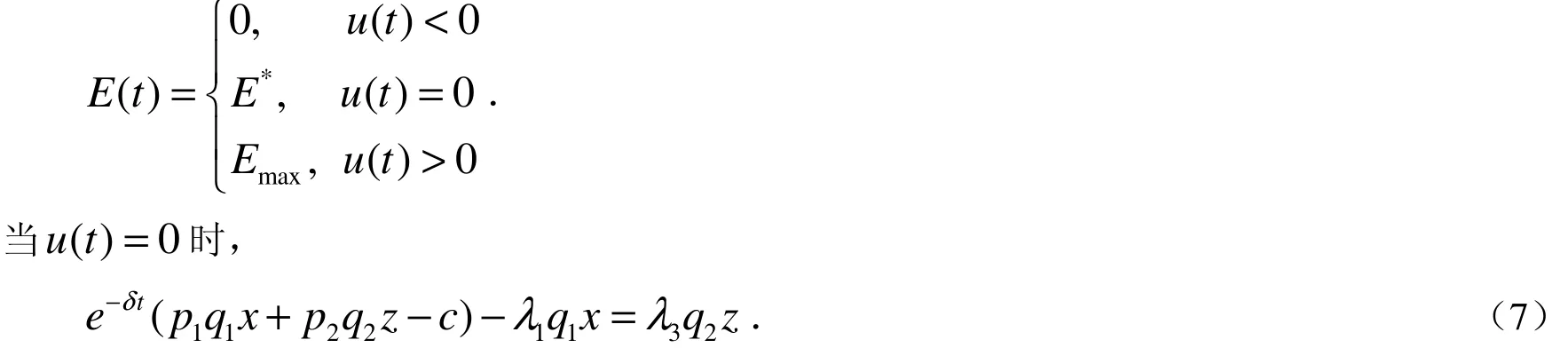
将（7）式、（11）式和（12）式分别代入方程（8）、（9）、（10）中，经过计算可得：

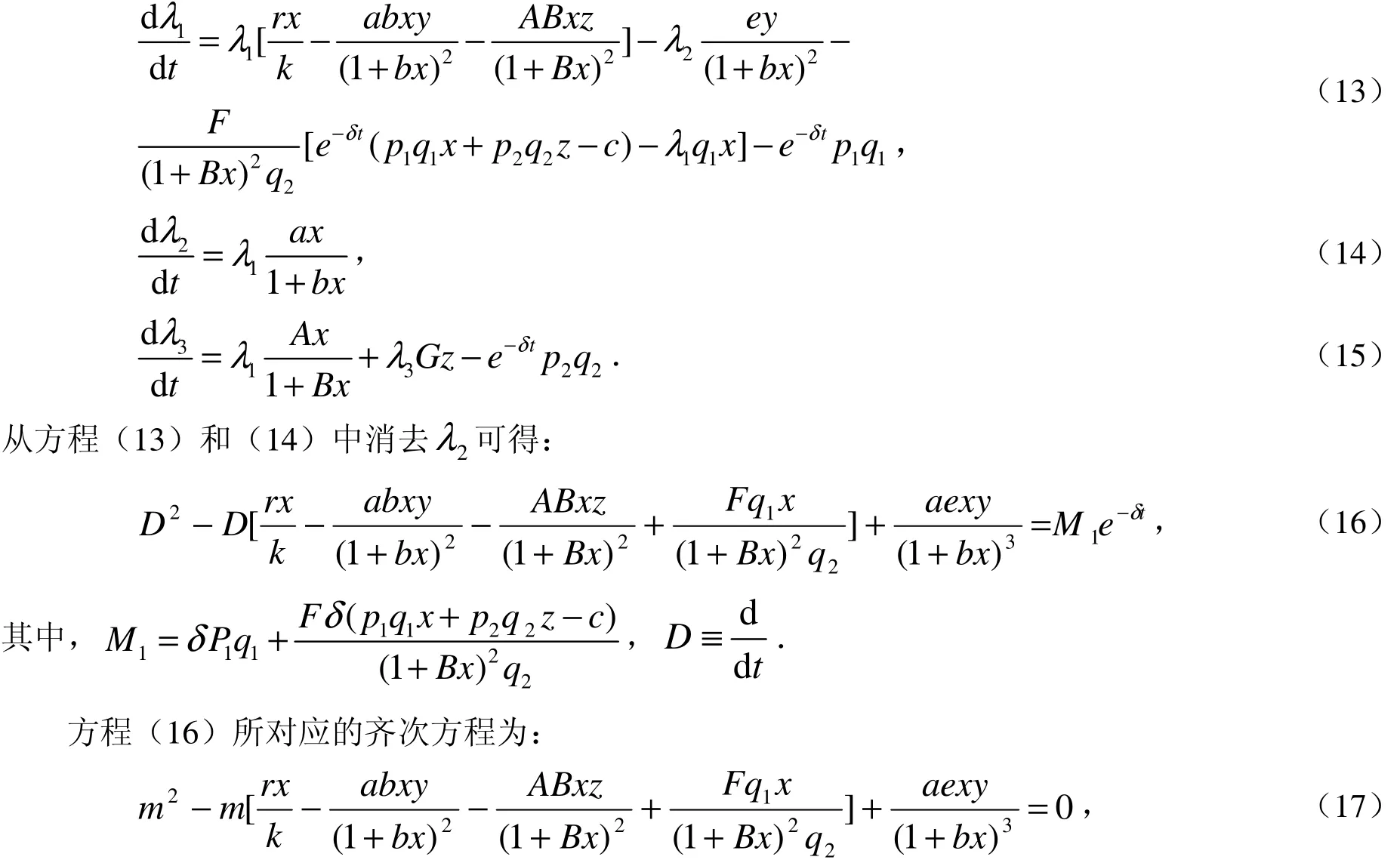
这是一个关于m的二次方程.由根与系数的关系可知：

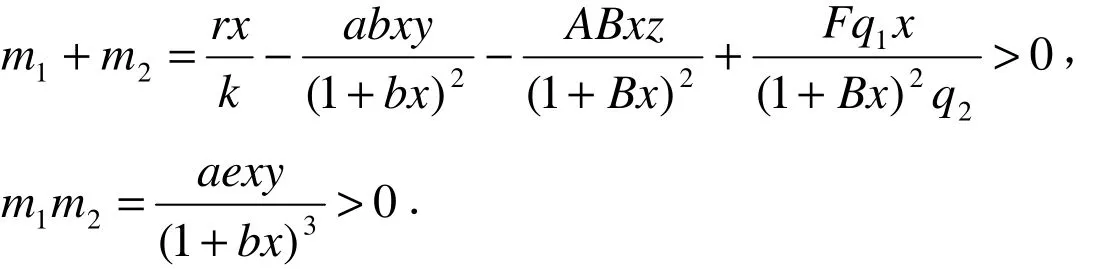
因此，方程（17）的两根m1,m2为正实根或具有正实部的虚根.方程（16）的解的形式为：

[1]Holling C S. The functional response of predator to prey density and its role in mimicry and population regulation [J]. Memoirs of the Entomological Society of Canada, 1965, 45: 3-60.

[2]刘宣亮. 具有常数收获率和第 II类功能性反应的捕食系统可以至少存在两个极限环[J]. 生物数学学报, 1994, 9(5): 192-199.

[3]张娟, 马知恩. 一类具有Holling II类功能反应且两种群具有密度制约的捕食系统极限环的唯一性[J]. 生物数学学报, 1996, 1(12): 26-30.

[4]朴仲铉, 薛春艳. 食饵种群具有收获(存放)率的II类功能性反应模型的定性分析[J]. 生物数学学报, 1997, 12(2): 140-144.

[5]Kar T K, Chaudhuri K S. On non-selective harvesting of two competing fish species in the presence of toxicity [J]. Ecological Modeling, 2003, 161: 125-137.

[6]Kar T K, Swarnakamal M. Influence of prey reserve in a prey-predator fishery [J]. Nonlinear Analysis, 2006, 65: 1725-1735.

[7]肖海滨. 双密度制约的Holling II型捕食动力系统的定性分析[J]. 生物数学学报, 2006, 21(3): 334-340.

[8]陈滨, 王明新. 一类三种群捕食模型的正解[J]. 数学物理学报, 2008, 28(6): 1256-1266.

[9]Ruan S, Ardito A, Ricciard P, et al. Coexistence in competition models with density-dependent mortality [J]. Biological modeling, 2007, 330: 845-854.

[10]王朝珠, 秦化淑. 最优控制理论[M]. 北京: 科学出版社, 2003: 83-87.

Stability and Optimal Harvesting Policy of Predator-prey System with Holling II Function Response

DING Jianhua, LUO Zhixue, ZHU Qingquan
(School of Mathematics, Physics and Software Engineering, Lanzhou Jiaotong University, Lanzhou, China 730070)

The Predator-prey System with Holling II function response was studied by using the theory of differential equation. Under appropriate assumption, the locally asymptotical stabilty of system’s positive equilibrium was proved by applying Routh-Hurwitz criterion, the globally asymptoticical stability of the positive equilibrium was proved by constructing a Liapunov function and the optimal harvesting policy for permanence of resource stock was obtained by applying Pantryagin’s Maximum Principle.

Predator-prey System; Holling II Function Response; Positive Equilibrium; Stability; Optimal Harvesting Policy

(编辑：王一芳)

O175.14

A

1674-3563(2011)01-0001-08

10.3875/j.issn.1674-3563.2011.01.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2010-05-09

国家自然科学基金(10771048)

丁建华(1986- )，女，甘肃天水人，硕士研究生，研究方向：生物数学，最优控制理论