仪器定量分析中几个问题的探讨
2011-01-11邓勃
邓 勃
(清华大学化学系,北京 100084)
仪器定量分析中几个问题的探讨
邓 勃
(清华大学化学系,北京 100084)
详细介绍了分析方法的评价指标,包括检出限、测定限、灵敏度、精密度、准确度、动态范围和线性范围、抗干扰能力等,单因素优化方法与加标回收实验评定测定结果准确度的可靠性,并就分析工作中遇到的一些实际问题进行了讨论。
检出限;测定限;灵敏度;精密度;准确度;动态范围和线性范围;抗干扰能力;优化;加标回收
O657
A
2095-1035(2011)02-0001-05
1 引言
近年来,环境污染和保护、食品安全、医疗保健等越来越受到人们的普遍关注,分析检测工作也因此受到社会、各级政府和检测部门前所未有的重视。分析工作者每年为社会提供了大量的检测数据,在各种公开的学术期刊上发表了许多研发报告,为促进科学技术的进步、国民经济和生产的发展、保障人民的健康都做出了重要的贡献,与此同时,也促进了分析检测技术的快速发展。从读到的很有限文献和检测报告中发现,存在一些值得有待进一步深入探讨的共性问题,希望引起大家的重视。本文拟针对仪器定量分析,与分析工作者共同探讨分析方法评价、试验参数优化和加标回收实验的可靠性等方面的问题。
2 分析方法的评价
随着分析仪器和分析技术的进步,新的分析方法不断出现。面对着大量的分析方法,如何选择已有的或研发新的适合于完成特定分析任务的分析方法,是分析人员所关注的问题。这里首先遇到的一个问题是用什么标准或参数来评价一个分析方法。评价一个分析方法至少包括三方面:分析方法的检测能力、用该分析方法测得结果的可靠性与分析方法的适用性。
2.1 良好的检测能力
分析方法的检测能力决定了分析方法能否满足实际分析要求,是评价分析方法的基本指标。表征分析方法检测能力的参数有检出限(detection limit)、测定限(determination limit)和灵敏度(sensitivity)。
2.1.1 检出限
分析方法的检出限是指能用该方法以适当置信度检出被测组分的最低质量或最低浓度。本定义中所谓‘检出’是指由最低检出质量mDL和最低检出浓度cDL产生的分析信号显著地区别于不含被测组分的‘空白’样产生的‘空白’噪声,而且是以所要求的置信度(通常取置信度99.7%)检出的,因此,可由最小检测信号值与‘空白’噪声导出检出限的关系式。

式中ADL是在检出限水平测定的分析信号平均值,Ab是‘空白’样产生的信号平均值,sb是‘空白’噪声(标准偏差),b是校正曲线在低量值区域的斜率。
测定量值在检出限水平的样品,测定值的离散性较大,有些文章因此就认为检出限是一个定性指标。定性指标通常只是就被测组分在样品中是否存在做出结论,而由上述检出限定义可知,检出限能用量值定量表征,因此,不能认为检出限是一个定性指标。检出限也不是实际测定的最小质量或最小浓度值,而是一个由分析信号以一定置信度导出的统计值。
值得注意的是,第一,由上述关系式计算的检出限,取置信系数k=3,置信度为99.7%,是在测定误差遵从正态分布的条件下才成立,而在实际测定中,是在低质量或低浓度水平进行有限次测定,测定误差更可能是遵从非正态分布,置信度达不到99.7%。第二,由式(1)从差值(ADL-Ab)导出检出限时,设测定‘空白’样品信号Ab的标准偏差为sb,测定量值为检出限水平的样品分析信号ADL的标准偏差亦为sb,按照误差传递原理,测定差值(ADL-Ab)信号的标准偏差应为s=2sb=1.414sb,要使信号ADL能以置信度为99.7%显著地从Ab中检出,至少应使(ADL-Ab)≥3s=4.24sb。第三,在实际工作中,基体匹配的‘空白’样品不容易找到,通常用不含被测组分的纯溶液作为‘空白’样品,进行若干次(也不是进行足够多次比如20次)测量,测得的标准偏差sb往往偏小,求得的检出限值比预期的要好些。要使量值在检出限水平的测定值有足够的可靠性,计算检出限的置信系数k至少要大于4.24sb。
分析方法的检出限受分析仪器能检测最小信号能力的制约,也依赖于分析条件的优选。检出限可以作为分析人员选择和评估分析方法能否满足实际分析工作要求的依据,要对在不同仪器和条件下得到的检出限进行定量比较,在事实上存在一定的困难。
2.1.2 测定限
测定限是以一定置信度实际能定量测定的被测组分的最小质量或最小浓度。它不仅受测定噪声的制约(这一点与检出限是类似的),也依赖于‘空白’绝对值(这一点是与检出限不同的)。由于分析过程中试剂、器皿和环境的污染,‘空白’值增大,会增加有用分析信号与‘空白’信号分辨的困难。只有当有用分析信号比‘空白’信号大到一定程度后,才能可靠地从‘空白’信号中分辨出有用分析信号。假定ADL/Ab=k为从‘空白’信号中分辨出有用分析信号的阈值,代入⑴式,得到的定量测定被测组分的最小质量或最小浓度分别是

‘空白’噪声越大,要可靠地从‘空白’信号中分辨出有用分析信号,需要k值越大,测定限越高;‘空白’信号值Ab越大,测定限也越高,从高‘空白’值比从低‘空白’值中分辨小分析信号更困难,这是不难理解的。因此,在实际测定中减小玷污、降低‘空白’信号值Ab对改善测定限具有重要意义,这也是分析痕量组分时要求给出‘空白’值的原因。
2.1.3 灵敏度
灵敏度是指被测组分质量或浓度改变一个单位时分析信号的变化量,即校正曲线的斜率,反映了对量值变化的分辨和检测能力。灵敏度不仅影响检出限,也影响校正曲线的线性范围。灵敏度受仪器施加于检测器上负高压的影响,施加的负高压高,会提高灵敏度,但同时使检测器的噪声增大,因此,依靠提高施加于检测器负高压来提高灵敏度,以期改善检出限是不可取的。而且,还会增大分析信号的不稳定性。只有通过优化实验条件提高灵敏度,才对改善检出限有效。
2.2 测定结果的可靠性
测定结果的可靠性要求测定值离散性小,测定平均值尽可能接近真值,即平均值是真值的无偏估计值。因此,精密度高、准确度好就成了选择分析方法的主要依据和评价分析方法的主要指标。
2.2.1 精密度
精密度(p recision)是指多次测定时各次测定量值之间相互一致的程度,反映测定过程中随机误差的大小,通常用标准偏差或相对标准偏差表示。精密度与系统误差无关,不需在消除系统误差的前提下去求精密度。但是,精密度与被测定的量值水平有关,报告标准偏差或相对标准偏差必须说明是在什么量值水平下得到的,而且注明重复测定次数。不指明被测定量值水平的标准偏差或相对标准偏差是不能说明问题的,严格地说是没有实际意义的。
重复性也是测定量值之间相互一致程度的量度,但精密度不等同于重复性。重复性r有专门的定义,是指在同一实验室同一分析人员用同一分析仪器和方法对同一量相继进行两次测定时,两次重复测定值按指定概率的容许差,在置信度为95%时,r=1.962sr=2.83sr,sr是单次测定的标准偏差,2sr是两次重复测定值之差值的标准偏差。在原子光谱分析仪器性能评定中,有一个稳定性指标,现在的评估方法是连续测定30 min和2 h,考察吸收值的波动性,分别作为仪器短期稳定性和长期稳定性指标。这里有一个误解,将长期稳定性误解为长时间稳定性。连续测定时间由30 min延长至2 h,还是长时间稳定性,而不是长期稳定性,仍用标准偏差表征。长期稳定性的含义是指在不同时间段内,按一定程序进行一定时间的相继测量,各段时间之间测定量值的一致性,用并合标准偏差¯s表征。

式中m是不同时间段,ni是第i个时间段的测定次数,xij是第i个时间段第j次测定值,¯xi是第i个时间段ni次测定的平均值。
2.2.2 准确度
准确度(accuracy)是测定的量值平均值与真值相符合的程度,表征测定值的系统误差,以误差或相对误差表示。现在国内绝大多数分析化学教材、文献和有关国标中都采用准确度这一术语表述系统误差,但仍有些文章和国标中使用正确性表示系统误差,将准确度看成是正确性与精密度的综合。用正确性不如用准确度来表征系统误差更确切,从中文词义考虑,正确与错误是相对的,准确与不准确是相对的,一个测定值偏离真值较远,误差较大,可以说测定值不准确,但不能说测定值是错误的。全国科学技术名词审定委员会第二届化学名词审定委员会在修订的化学名词术语中,也采用了准确度一词,定义为在一定测量条件下测量值与被测定量的真值之间一致的程度。
如果以正确性表示系统误差,将准确度看成是正确性与精密度的综合。正确性自然用误差或相对误差表示,那么准确度以什么量值表示?正确性与精密度如何综合?准确度与合成标准不确定度又是什么关系?都值得考虑和商榷。
无论从用词的确切性,还是依照约定俗成的原则,采用准确度比正确性表征系统误差更科学合理。
2.3 方法的适用性
任何一个分析方法必须实用,这是对分析方法的基本要求。适用性要求分析方法有较宽的校正曲线线性范围(linear range)或动态范围(dynamic range),有较强的抗干扰能力(anti-interference ability),能适用于多种类型的样品,且简便和易于操作。
现在有些文献中,将校正曲线的动态范围与线性范围等同起来,事实上,校正曲线的动态范围与线性范围是有区别的,不能混淆。前者指响应值随测定量值基本呈现线性变化,在校正曲线的高量值区域常略有弯曲。应该指出的是,用相关系数检验合格的校正曲线,只表明所建立的校正曲线在统计上是有意义的,确定的是校正曲线动态范围,如图1中的虚线,相关系数是r=0.9534,动态范围上限是0.48μg/mL。确定校正曲线的线性范围在统计上需进行拟合优度检验,如图1的实线,线性范围上限是0.16μg/mL。动态范围大于线性范围。
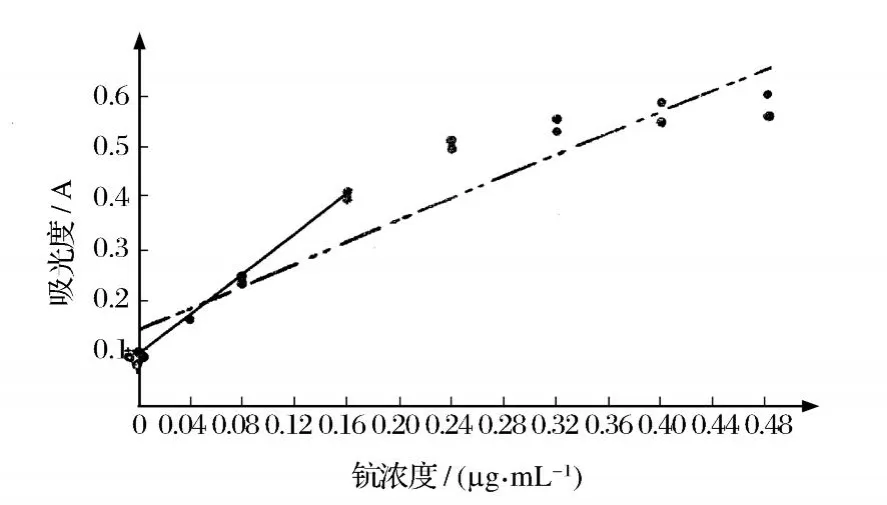
图1 校正曲线的动态范围与线性范围Figure 1.The dynam ic range and the linear range for a calibration curve.
抗干扰能力可用选择性系数,或更直接的用允许的干扰物质量表征。研究抗干扰能力时,不能忽略干扰组分之间的交互作用。干扰组分单独存在与其他干扰组分共同存在时产生的干扰效应是不同的,可能相互抵消,也可能协同增强。当因素之间存在交互效应时,应在因素共同存在的情况下考察干扰效应。
3 试验参数优化方法
研发新的分析方法,或采用已有的分析方法分析样品,都需要对影响分析结果的试验参数进行优化。试验参数的优化方法很多,如单因素轮换优化法、正交试验设计优化法、均匀设计优化法、单纯形优化法等,但在我国多数实验室分析人员最常使用的参数优化方法是单因素轮换优化法(single factor alternative op timization method),而使用多因素同时优化方法的还相当少见。单因素轮换优化法是固定其他参数不变,只改变一个参数的水平,求得该因素优化水平,将其固定在优化水平,再依次一个个参数进行优化,最后将各参数的优化水平组合在一起作为最佳测定条件。这种优化参数的方法简便,易于操作。但这种优化方法有两个主要的缺点。
(1)忽略了因素之间的交互效应。分析人员都知道,在分析中因素之间的交互效应是普遍存在的,在火焰原子吸收光谱法(FAAS)中,灯电流、燃气、助燃气、燃烧器高度、进样量等影响吸收值的因素中,灯电流与其它因素之间不存在交互效应,可用单因素轮换优化法优选最佳灯电流,而燃气、助燃气、燃烧器高度、进样量之间存在交互效应,固定不同因素的不同参数水平,得到的各参数的优化组合是不同的。如用FAAS法测定镍电解液中的铜,乙炔流量固定在1.5 L/min,合适的空气流量是9.0 L/min,乙炔流量固定在2.5 L/min,合适的空气流量是11.0 L/min。又如在石墨炉原子吸收光谱(GFAAS)分析中,灰化温度、灰化时间和进样量之间也存在交互效应,不同的进样量,在不同的灰化温度需要不同的灰化时间;在光度分析中,即使加入相同量的显色剂,也会因试液中酸度不同解离出来有效显色基团浓度不同,产生的显色强度不同。在因素之间无交互效应时,单因素轮换优化法与多因素同时优化结果是一致的。
(2)单因素轮换优化法得到的优化条件是一定条件下的局部优化而非全局最优条件,只有将单因数优化得到的几组局部优化条件再进行二次优选,才能求得全局或接近全局优化条件。在现在发表的一些文章中,随意将单因素轮换优化条件组合说成是最佳测定条件是不恰当的。
4 用加标回收率评定测定结果准确度的可靠性
分析测试是为科研和社会提供第一手原始数据和资料,是作出科学、公正结论的基础。当测试结果中存在系统误差产生的偏倚,使测定结果无法溯源,甚至导致错误的结论。因此,在分析测试中需要用合适的方法来评估测定结果的准确度。评估测定结果准确度最直接有效的方法是使用标准物质(或质控样),将基体、量值、赋存形态与被测定试样相匹配的标准物质与试样,同时经历全分析过程,如果测得标准物质的量值在一定置信度下经t检验与标准物质的标准量值没有显著性差异,说明测定方法和测定过程不存在系统误差,反之,表明测定方法、或测定过程、或测定方法和测定过程同时存在系统误差。通过标准物质可将测定结果溯源到SI单位。采用标准分析方法和被检查的分析方法同时测定同一试样,比较两种分析方法的测定结果,如果两者的测定结果在一定置信度水平经t检验没有显著性差异,说明被检查的分析方法不存在系统误差,其测定结果是可靠的。但合适的标准物质和标准方法在许多情况下并不一定能找得到,特别是在研究新材料或新分析方法时,没有标准物质或标准方法。因此,在更多情况下都采用加标回收法来评定测定结果的准确度。
在分析测试中,影响测定结果准确度的是系统误差产生的偏倚,分为固定偏倚和相对偏倚,分别由固定系统误差和比例系统误差产生。如果测定结果中存在固定偏倚,就相当于在样品测定值x0中加入了一个固定量xa,等效于校正曲线平移一个xa量,而斜率不变。xa不随加标量而改变,加标前、后都增加或减小了相同的一个量xa,加标前后两次测定值相减,固定偏倚被低偿,加入的标准量值的回收率理所当然是100%。由此可见,加标回收实验不能发现固定偏倚,加标回收率100%也不能证明加标前的测定量值x0不存在固定偏倚。如果测定结果中存在相对偏倚,校正曲线截距不变而斜率随着标准加入量发生变化,这时回收率将不再是100%,也就是说,加标回收能发现比例系统误差产生的相对偏倚。加标回收只能对加标量值测定是否存在相对偏倚做结论,而不能直接对加标前的测定量值是否存在相对偏倚做出结论。
加标回收实验的目的是要通过加标量的回收率来评定加标前的测定量值的可靠性。如果加标前、后量值水平的回收率是一样的,局外因素对回收率的影响不随加入量而改变,就可以用加标量的回收率推论加标前的测定量值的回收率,这就要求加入量与原含量必须是很接近的,加标量通常是原测定量的相同量值或是原测定量值的2~3倍。因为局外因素对量值相差很大的两个不同含量水平的回收率产生的影响是不同的。
对于在实际工作中如何来分辨固定偏倚或相对偏倚?可用纯溶液和样品溶液同时建立校正曲线,如果两条线是平行的,表明只存在固定偏倚,不能用加标回收实验来评定加标前测定量值的准确度;如果两条线是交叉的,可用加标回收实验来评定加标前测定量值的准确度。
下面通过一个实例来进一步具体讨论加标回收的可靠性问题。某人用ICP-AES测定铅锡焊料中铁,测定值是3.7μg,加入50.0μg铁标准后,测定值是51.2μg。回收量是51.2-3.7=47.5μg,回收率是95.0%。该文作者因此做出结论:测定结果不存在系统误差。现在来分析这一实验结果及其结论。
(1)加标后进行第二次测定,损失了2.5μg铁,都归属于新准确加入的50μg铁的损失,回收率为95%。这意味着第一次测定值3.7μg是准确的。前面提到,加标回收的目的就是要证明测定值3.7μg是否准确?现在在证明之前事先就假定测定值3.7μg是准确的,将要证明的当做证明的前提,在逻辑上是不合理的。从实际考虑,如果测定值3.7μg是准确的,就用不着再进行加标回收实验来证明测定值3.7μg是否准确。
(2)加标50μg铁是准确的,第一次测定值3.7μg是待证实的,加入50μg铁后再对53.7μg铁进行测定,损失2.5μg铁,既有新加入50μg铁的贡献,又有原测定量值3.7μg铁的贡献(损失量是随被测定量值水平而改变),损失的2.5μg铁应归属于总量53.7μg铁中的损失,回收率应是 51.2/53.7= 95.34%,而不应是95%。回收率计算结果虽然相差不大,但涉及到回收率的计算方法,值得考虑和商榷。
(3)如果产生的偏倚是由固定系统误差引起的,损失量是固定的,不再随加入量而改变,准确加入50μg铁,回收也应是50μg铁,回收率应是100%。即使这样,也只能就所加铁标量而言不存在系统误差,也不能说明加标前测定值不存在系统误差。
(4)实验设计不合理,加标量选择过大。当存在比例系统误差时,产生的相对偏倚是随铁量值水平而改变的,高量值水平与低量值水平的回收率是不一样的,将50μg铁水平的回收率代表3.7μg铁水平的回收率是有问题的。加标量应选择在加标前测定量值的附近,在这种情况下,用加标回收率代表加标前测定量值的回收率一般是可以接受的。这是应用加标回收实验评定测定值准确度的前提。
5 结语
在研发新的分析方法时,应给出评价分析方法的全面评价指标。检出限是一个由分析信号导出的统计值,是一个定量指标。测定限受‘空白’绝对值的限制。报告标准偏差或相对标准偏差必须说明是在什么量值水平下得到的,而且注明重复测定次数。长期精密度不同于长时间精密度,用并合标准偏差表征。采用准确度比正确性表征系统误差更科学合理。校正曲线的动态范围与线性范围是有区别的,不能混淆。研究抗干扰能力时,不能忽略干扰组分之间的交互作用。
单因素轮换优化法是简便有效的优化方法,在因素之间无交互效应时,与多因素同时优化结果是一致的。单因素轮换优化法得到的优化条件是一定条件下的局部优化而非全局最优条件,只有将单因数优化得到的几组局部优化条件再进行二次优选,才能求得全局或接近全局的优化条件。
用加标回收实验检查和评定测定量值的准确度,只适用于存在比例系统误差产生相对偏倚的情况,不能发现固定系统误差产生的固定偏倚。加标量应选择在加标前测定量值的附近,这是用加标回收率推论加标前测定值回收率的前提。
[1]邓勃.分析测试数据的统计处理方法[M].北京:清华大学出版社,1995:291-303.
[2]考尔卡特 R,鲍迪著 R.分析化学工作者用统计学[M],王克谦,张华山,译.邓勃,校.北京:科学出版社,1989: 37-87.
[3]国家标准化管理委员会.GB/T 6378-1986测试方法的精密度,通过实验室间试验确定标准测试方法的重复性和再现性[S].北京:中国标准出版社,1986.
[4]邓勃.实验设计与优化方法[J].分析科学学报,1996,12 (2):157.
[5]邓勃,王小芹.光谱分析中的试验设计方法[J].光谱学与光谱分分析,1983,3(3):53.
The Discussion of Some Problems in Quantitative Instrumental Analysis
DENGBo
(Chemistry department,Tsinghua University,Beijing100084,China)
The evaluation parameters for an analytical method,including detection limit,determination limit,sensitivity,p recision,accuracy,dynamic range,linear range and anti-interference power etc.,were introduced in detail.The single factor alternative op timization method was reviewed and the reliability of accuracy assessment using the standard addition experiment w as evaluated.In addition,some p ractical p roblem s that encountered during instrumental analysis p rocesses were discussed aswell.
detection limit;determination lim it;sensitivity;p recision;accuracy;dynam ic range;linear range;anti-interference ability;op timization;recovery of standard addition
10.3969/j.issn.2095-1035.2011.02.0001
2011-02-11
2011-03-12
邓勃,男,清华大学教授,主要从事光谱分析。E-mail:dengbo@mail.tsinghua.edu.cn
