奇异性分析在赤峰地区地球化学异常识别中的应用

2011-01-10刘洪涛蒋艳明吴铁军常德良

地质找矿论丛 2011年3期

刘洪涛，蒋艳明，吴铁军，常德良

（辽宁省冶金地质勘查局地质勘查研究院，辽宁鞍山 114002）

0 引言

勘查地球化学方法是矿产勘查的重要手段，确定地球化学异常是勘查地球化学领域的首要问题，统计学方法在地球化学异常识别中起着重要作用。传统的异常下限计算方法是以地球化学数据服从正态或对数正态分布为假设前提，一般采用平均值（或几何平均值、众值或中位数）作为地球化学背景值，以背景值加n倍标准离差作为异常下限值，进而圈定地球化学异常，但受到复杂的地质环境和成矿过程的影响，地壳中的元素分布往往不服从正态分布或对数正态分布，对异常识别效果有很大影响。而奇异性分析方法考虑到地球科学的许多现象具有自相似性或者广义自相似性，兼顾了样本空间的变异性，突出了叠加异常和弱异常地区。本文将介绍奇异性分析方法及其在内蒙古赤峰地区地球化学异常识别中的应用。

1 统计学方法研究现状

在地球化学异常研究中，传统的统计学方法主要利用地球化学元素浓度值的概率分布和多变量间的相关关系确定地球化学异常。这些方法属于非空间统计方法，它们忽视了样本的空间关系和自相关结构。而因子分析等空间统计方法则考虑了样本的空间相关性和变异性，有效地解决了一些应用中存在的问题，但在分解复杂背景和叠加异常、弱异常提取等方面仍具有一定的局限性［1］。

近年来，分形和多重分形包括奇异性分析等现代非线性理论被应用于矿产资源勘查领域。奇异性事件是指发生在很小的时间或者空间间隔中产生巨量能量释放或者物质的超常富集的事件，对于成矿过程，尤其是与热液活动有关的过程，往往呈多期次重复性成矿，这种空间上多次矿化的叠加作用最终可导致复杂的微量元素空间奇异性分布。

传统统计学方法需要以数据的分布状态为前提，只有当原始数据服从或近似服从正态分布或对数正态分布时，才能计算出异常下限，进而圈定地球化学异常。由于各种构造运动和成矿作用等地质过程对元素迁移富集规律的影响，成矿微量元素往往不服从正态分布或对数正态分布，这就对地球化学异常识别产生了很大的影响。而奇异性分析方法不以数据的分布状态为前提，考虑到地球科学的许多现象具有自相似性或者广义自相似性，其结果具有奇异性分布，奇异性分析刻画出地球化学场的局部特征，从而确定出整体地球化学异常特征，不但考虑到样本空间的相关性，而且兼顾了样本空间的变异性，因此突出了叠加异常和弱异常地区。

2 奇异性分析的应用过程

地球化学场的奇异性特征可以采用幂律分布进行度量，由指数函数ρ（ε）∝εα－2来表达［2］，这里ρ（ε）是一种基于尺度ε的量或场，元素平均密度与度量范围大小ε×ε的关系表明，当奇异性指数α＝2时，平均密度与度量范围的大小无关，反映区内背景分布往往与面积性的地质体有关；当α＞2时，ρ（ε）随着ε的减小而减小，反映与局部地质因素有关的元素含量贫化现象；当α＜2时，ρ（ε）随着ε的减小而增加，反映与局部地质因素有关的元素含量富集现象。

奇异性分析方法的关键在于计算出每个采样点的奇异性指数。奇异性指数可按如下步骤计算：由小到大确定滑动平均窗口：l1×l1，l2×l2，…，lm×lm，得到m幅滑动平均图，记为Z1，Z2，…，Zm；取L＝max｛li｝＝ln，其中i＝1，2，…，m；以log（Zi×（li/L）E）为因变量，log（li/L）为自变量，遍历空间所有位置进行最小二乘拟合，回归直线的斜率即该位置处的α值［3］（具体计算过程及计算机程序将另文介绍），并转换成Δα＝E－α，进而得到奇异性指数分析所识别的异常分布形态。

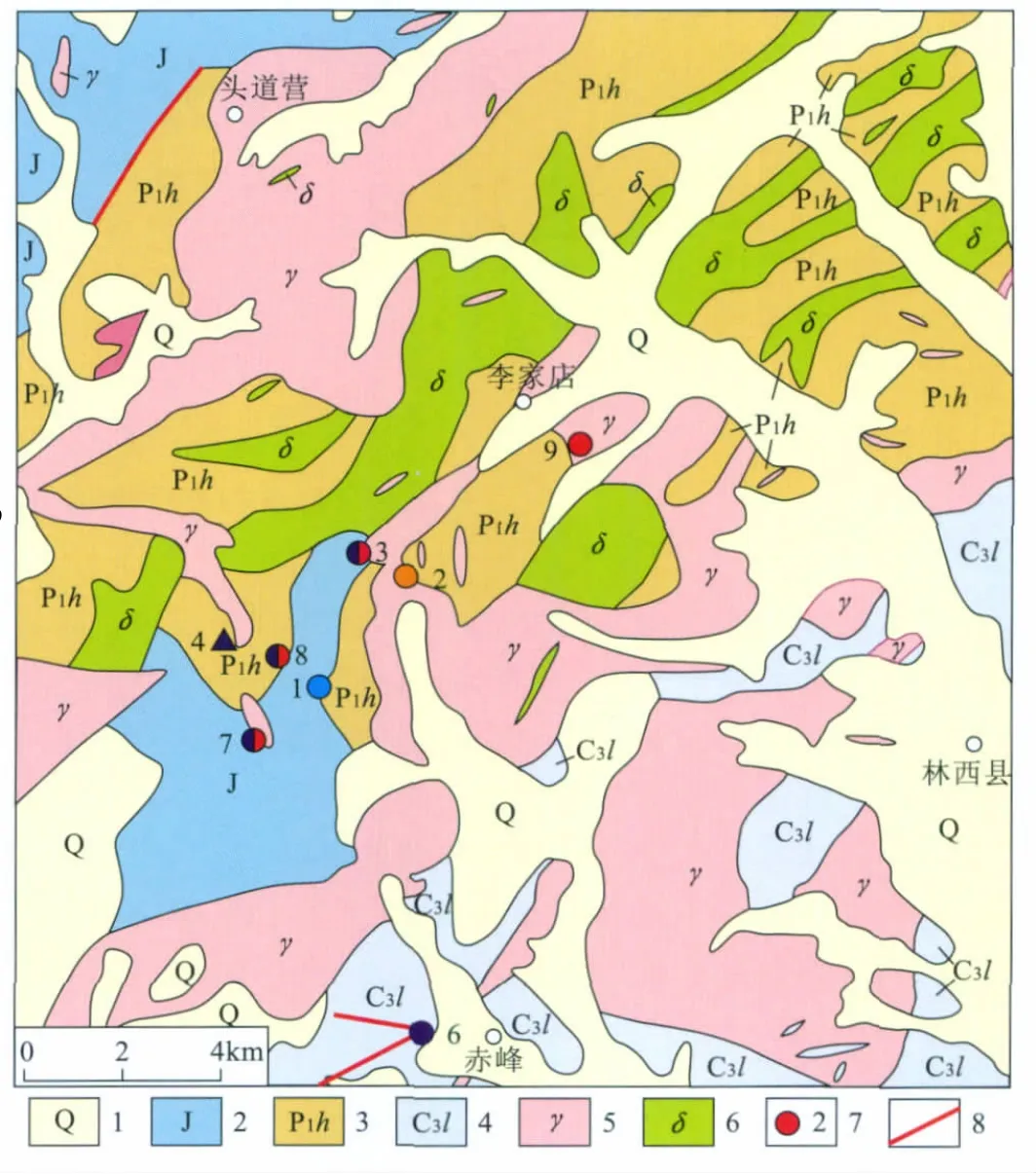
图1 研究区地质略图Fig.1 Sketch map of geology in the study area

3 奇异性分析在赤峰地区的应用

研究区位于内蒙古赤峰市林西县西部，地处阴山及大兴安岭两个成矿单元，且为环太平洋多金属成矿带的外带，属中高山区，境内山脉为大兴安岭支脉，最高海拔1 858 m，最低海拔870 m，地势西北高东南低。区内出露的地层有古生界石炭系、二叠系，中生界侏罗系及新生界第四系。研究区内构造较发育，主要为褶皱构造和断裂构造。褶皱构造有华力西晚期刘家营子—热水汤背斜，其两翼发育有3个次级背斜和4个次级向斜；断裂构造主要有EW向的林西以西正断层，NE向的白音皋断裂，发育在二叠系为黄岗梁组与中生界中侏罗统之接触带上（图1）。研究区内，分布有金矿、铅矿、铅锌矿、多金属矿等矿（化）点9个。

本区3 016个水系沉积物样品分析数据的分布状态（图2）表明，该区金元素数据既不服从正态分布，也不服从对数正态分布，不满足应用传统地球化学异常识别方法的条件。因此，应用奇异性分析方法进行地球化学异常识别。

首先计算出奇异性指数。选取的滑动平均窗口大小序列为3×3，5×5，…，13×13，得到6幅滑动平均图，记为Z1，Z2，…，Z6；取L＝max｛li｝＝13，其中i＝1，2，…，6，以log（Zi×（li/L）2）为因变量，log（li/L）为自变量，遍历空间所有位置进行最小二乘拟合，这里由于数据为二维空间数据，所以取ε＝2，得到每个样品点金元素的奇异性指数，并转换成Δα＝E－α，得到奇异性指数分析所识别的异常分布形态（图3）。

奇异性分析得到的异常分布形态表明，高含量地段主要集中在研究区中南部和东北部，异常中心明显，分带性显著，具有一定线性排列特征，与已知金矿床和矿点的分布吻合较好。对该区水系沉积物样品金元素数据进行传统地球化学异常分析，得到其分布形态（图4）。

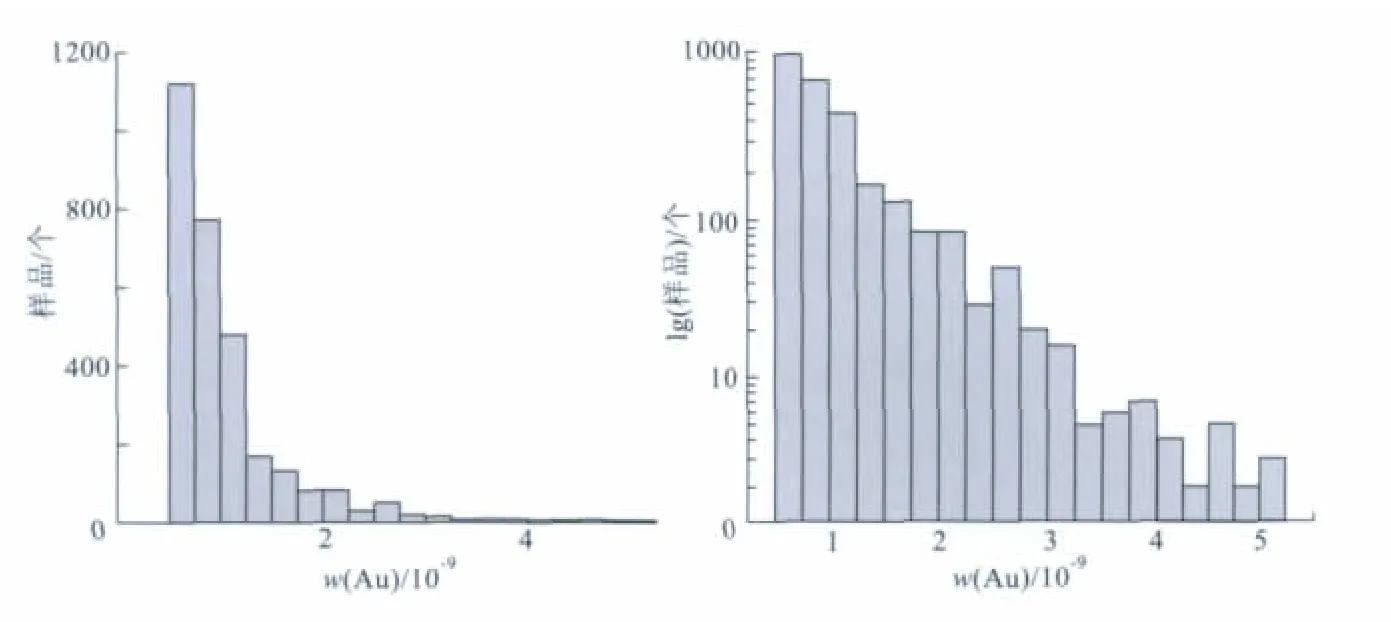
图2 金元素分布状况Fig.2 Distribution of Au

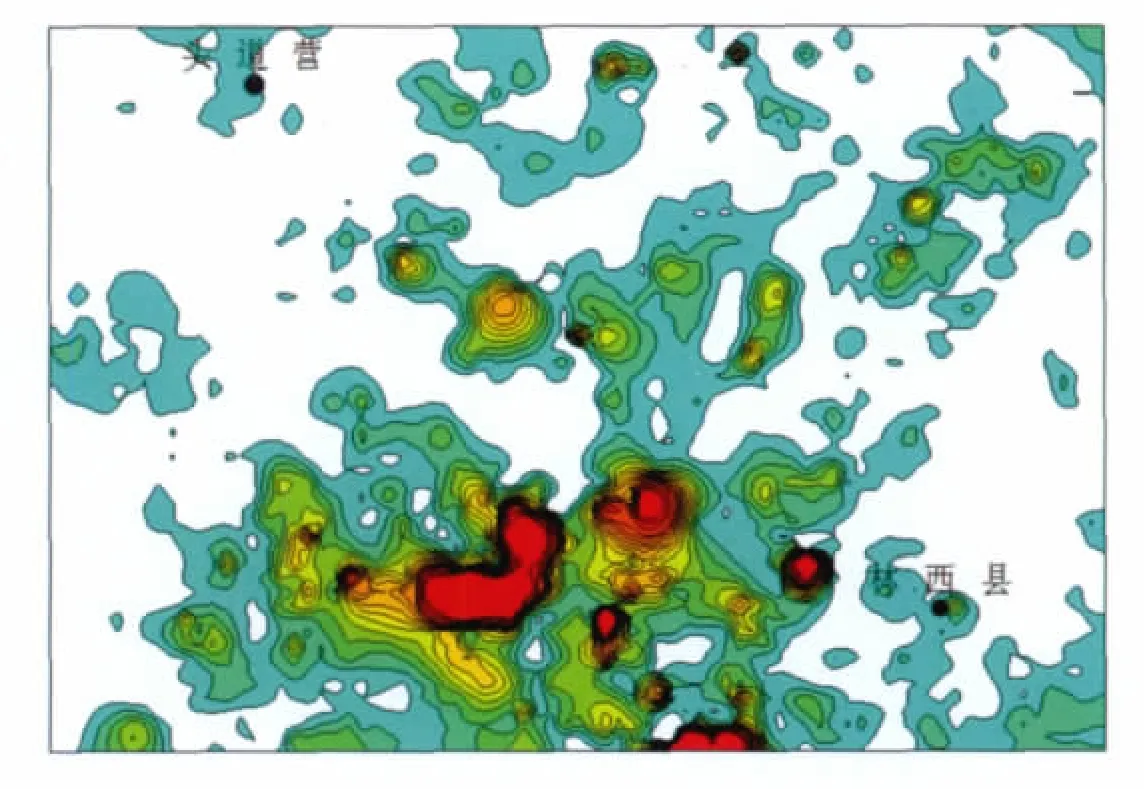
图3 奇异性指数分布Fig.2 Distribution of singularity index

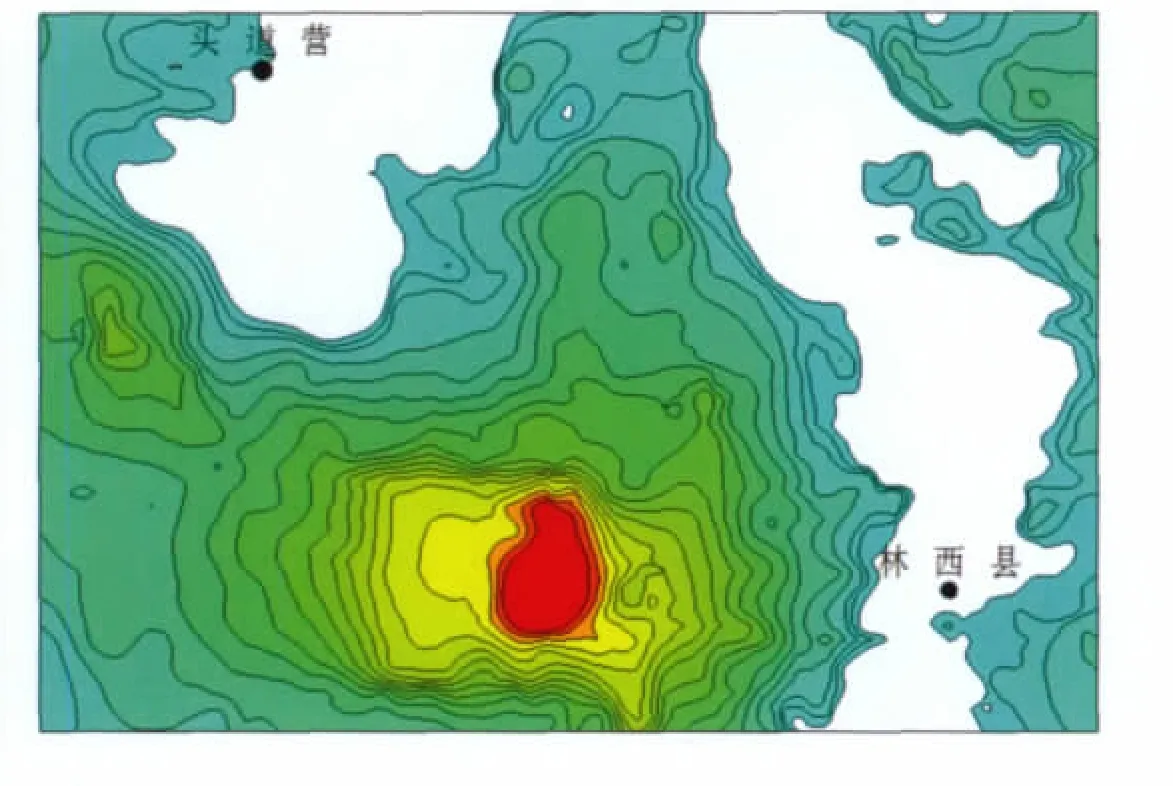
图4 传统方法识别的异常分布Fig.4 Anomalies distribution by recognized tradition method

对比两种方法分析的异常分布形态，传统统计分析方法能够确定主要异常区，但忽视了样本的空间关系和自相关结构，圈定的异常多处浓集中心被弱化，漏掉了许多有价值的地球化学信息；奇异性分析方法考虑到了样本的变异性，确定的异常特征更明显，浓集中心更加清晰，强化了弱异常地段的矿化富集信息，不但对大面积异常区解剖得更加准确，而且异常地段的分布规律也更加清楚。奇异性分析可以更方便地分析研究区构造方向和地球化学元素的迁移和富集规律；对于勘查地球化学数据来说，少数具有奇异性样品的识别更能突出弱化异常地段，这才真正具有预测找矿的意义，这也是传统的统计学方法不能有效地识别与矿有关异常的主要原因。