X型钢管相贯节点抗弯极限承载力的影响因素分析
2011-01-10廖贤
廖 贤
(成都大学城乡建设学院,四川成都 610106)
0 引 言
钢管结构设计中的一个难点是相贯节点的设计,由于节点区域几何和材料特性比较复杂,应力集中较为严重,且影响因素繁多,破坏形式多样,因而不能仅依靠力学理论推导来分析节点的受力状况.我国《钢结构设计规范》(G B50017-2003)[1](以下简称《规范》)10.3.3条规定:主管和支管均为圆管的直接焊接节点承载力应按下列规定计算,其适用范围为,0.2≤β≤0.2;di/ti≤60,d/t≤100,θ≥30°,60°≤φ≤120°;同时,为保证节点处主管的强度,支管的轴心力不得大于本条规定中的承载力设计值.由此可见,《规范》仅仅给出了钢管相贯节点各支管轴向承载力的计算公式,缺乏对节点抗弯极限承载力规定.这是由于目前《规范》中钢管相贯节点的承载力计算公式是依据Makino[2]于1996年建立的圆钢管相贯节点试验及有限元分析的数据库,以及20世纪90年代以来国内高校、设计院和建设单位结合工程实际所做的相贯节点试验结果[3].考虑到当时的实际状况,这些数据库和试验结果中钢管直径都不大于500 mm,远远小于现在许多实际工程中钢管相贯节点的尺寸.随着实际工程中钢管尺寸的增大,节点处的弯矩不容忽视,例如某体育场工程,其体育场罩棚采用拱支撑张拉膜结构体系,其中,主体结构采用在节点处直接相贯连接的钢管拱架结构,钢管拱架的总跨度达210 m,其钢管选用Q345B钢,采用高频焊管,该工程中采用了多种形式的大尺寸空间钢管相贯节点,节点种类达28种,其中平面节点有K型、X型,空间节点有TT型、X型、X型加单竖杆等.主管规格分别为Φ920 mm×16 mm和Φ813 mm×12 mm,支管规格为Φ219 mm×6 mm~Φ914 mm×16 mm.钢管尺寸如此之大,均已超过钢结构设计规范所依据的试验资料.因此,分析钢管相贯节点外抗弯极限承载力的影响因素很有必要.
1 X型钢管节点有限元模型的建立
对X型钢管相贯节点有限元模型的分析,本文采用shell 181单元三维四节点弹塑性壳单元.对于普通钢材,应力应变曲线经历线弹性阶段后,存在较为平缓的屈服平台,比较接近理想弹塑性,钢材屈服强度,fy=345 MPa,弹性模量,E=2.06×105MPa,泊松比,v=0.3.使用ANSYS程序中经典的双线性等向强化选项,材料的屈服准则遵守Von Mises屈服准则及相关的流动法则.在考虑材料非线性时,材料的应力应变曲线按两折线输入,材料的强化段采用切线模量为,E=1.03×103MPa,其应力应变曲线如图1所示.建立有限元模型时不考虑焊缝及残余应力对节点极限承载力的影响以简化模型.
计算模型的边界条件为:主管左边界按固定考虑,固定端采用线约束,右边界按滑动支座考虑;支管边界为自由端,支管和主管均由相交根部开始外伸3.5倍的管直径,以消除端部加载条件对节点区域的影响.

图1 材料的应力应变曲线
在模型计算时,影响钢管节点抗弯极限承载力的因素取下面两个:支管直径(di)与主管直径(d)比,β=di/d;主管半径与壁厚(t)比,γ=d/2t.
各因素对钢管节点抗弯极限承载力的影响采用单参数分析方法进行[4,5].具体做法是,取一系列模型,变化某一参数,而保持其他参数相同,使得模型抗弯承载力的差异仅由所变化参数的差异引起,从而获得节点抗弯承载力随各参数的变化趋势.计算时将模型分成两组,每组考虑一个因素变化对节点抗弯承载力的影响.
第一组模型考虑,β=di/d,对节点抗弯极限承载力的影响,结果如表1所示.

表1 第一组模型计算分析结果
第二组模型考虑,γ=d/2t,对节点抗弯极限承载力的影响,结果如表2所示.
2 钢管节点抗弯极限承载力分析
2.1 承载力的判定
钢管节点的破坏模式可能是以强度破坏达到其承载能力的极限状态,也可能是由于变形太大而不能继续承载.因此,对发生强度破坏的节点一般是取荷载位移曲线的极值点作为极限承载力,而对变形破坏的节点则采用变形极限的概念来判定承载力,即取节点变形达到变形极限时的荷载为极限承载力.对节点受弯矩荷载的情况,其弯矩转角曲线一般没有下降段.故本文采用Yura[6]的方法判定极限弯矩,管节点受弯矩荷载时,其变形极限取为80fyi/E,其中,fyi为支管屈服强度,E为弹性模量.

表2 第二组模型计算分析结果
2.2 各因素对钢管节点抗弯极限承载力的影响
2.2.1 参数β对抗弯承载力的影响.
图2是参数β对抗弯极限承载力(Mu)的影响曲线.
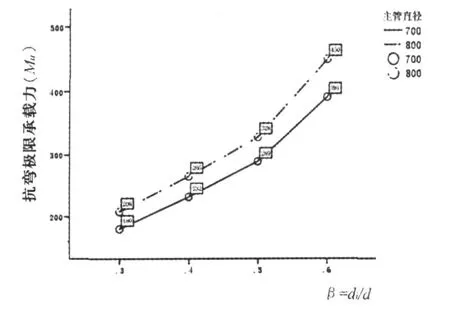
图2 参数β对抗弯极限承载力(Mu)的影响曲线
从图2可以看出,钢管节点抗弯极限承载力随参数β的增大而明显增大.对此,可通过一元非线性回归来进一步分析节点抗弯承载力随β参数变化的规律.本文比较了3种不同的曲线回归模型,分别是对数曲线、乘幂曲线和S曲线,通过对曲线回归模型的拟合效果,模型统计学意义的显著性和所求参数的t检验是否显著来优选,最后确定乘幂曲线拟合的统计意义最显著.乘幂曲线回归模型的未知参数分别为691.186和1.082,回归方程为,

2.2.2 参数γ对抗弯承载力的影响.
图3是参数γ对抗弯极限承载力Mu的影响曲线.

图3 参数γ对抗弯极限承载力(Mu)的影响曲线
从图3可以看出,管节点抗弯承载力随着γ的增大而明显的减小.同样,采用一元非线性回归来进一步分析节点受弯承载力随γ参数的变化规律.同样,本文比较了3种不同的曲线回归模型,分别是乘幂曲线、S曲线和growth曲线.通过对曲线模型的拟合效果,模型统计学意义的显著性和所求参数的 t检验是否显著的优选,最后确定growth曲线拟合效果最好,growth回归模型的未知参数分别为691.186和1.082,回归方程为,

3 结 论
通过分析X型钢管相贯节点考虑附加弯矩后的极限承载力,我们得出以下结论:在考虑几何非线性和材料非线性的情况下,通过单参数分析和力学原理推导分析了主管直径比,β=di/d,主管直径与壁厚比,γ=d/2t,对 X型钢管节点的抗弯极限承载力的影响,并用数理统计的方法证明,钢管节点受弯承载力随参数β的增加近于乘幂曲线的增长,随参数γ的增加近于growth曲线的增长.需要说明的是,本文只就参数β和γ分析了16个数值模型,鉴于影响钢管节点抗弯极限承载力的因素众多,对它的分析尚需做更多影响因素和更多模型的进一步的分析.
[1]中华人民共和国建设部.G B50017-2003钢结构设计规范[M].北京:中国计划出版社,2003.
[2]Makino Y,Kurobane Y,Ochi K,et al.Database of Test and Numerical Analysis Results for Unstiffened Tubular Joints[M].New Y ork:Elsevier Inc,1996.
[3]钢结构设计规范编制组.钢结构设计规范专题指南[M].北京:中国计划出版社,2003.
[4]廖贤.大尺寸空间KK型圆钢管相贯节点的极限承载力分析[D].重庆:重庆大学,2009.
[5]邱国志.圆钢管X型相贯节点刚度及其对结构整体性能的影响[D].上海:上海交通大学,2008.
[6]Yura J A,Zettlemoyer N,Edwards I F.Ultimate Capacity Equations for Tubular Joints[C]//12th Annual Offshore Technology Conference.Houston:OTC Press,1980.
