基于因子分析的地区信息化发展水平的聚类研究*

史 嵘，周念宇

(1．南京航空航天大学经济与管理学院，江苏南京210016;2．苏州科技学院经济与管理学院，江苏苏州215009)

近年来，信息化在国民经济和社会发展中发挥越来越重要的作用，信息化发展水平已经成为衡量国家综合国力与国际竞争力的重要标志。经过多年的信息化建设，我国的信息化整体水平已经得到了一定的提高。据国家信息化测评中心报告，近年来我国信息产业年均增长32%，高于同期全部工业年均增长速度近18个百分点，是40个工业行业中发展最快的。［1］但与国外发达国家相比，我国信息化水平还不高，尤其是地区之间信息化水平差异明显，信息产业对经济的“贡献”不平衡。因而在定量研究基础上科学评价及衡量区域信息化发展差异，对不同地区的信息化水平进行横向比较，为制定信息化建设的相关政策提供科学依据具有了较强的现实意义。

一、信息化发展水平的评价指标

对信息化的研究主要集中于在概念、内涵、经验借鉴、发展模式等定性方面，定量研究主要集中于企业信息化水平等微观层面，针对区域信息化水平的定性分析近年来并不多见。张明军［1］通过比较分析国际信息化水平的不同测度方法，选择相对适合中国的地区信息化评价指标体系进行分析，但所选指标侧重于信息化建设的基础建设部分，综合运用能力和发展水平难以显现。王梅英［2］侧重比较利用简单平均法、变异加权法和因子分析法对地区信息化水平及经济发展关系的分析的差异，所选指标6项指标十分有限。吴迎春［3］采用修正后的信息化水平综合指数法，对全国31个省市信息化水平进行测评分析。鉴于此，在综合以上文献研究的基础上，构建信息化发展水平的综合评价指标，利用因子分析方法和聚类分析方法，对我国各省市信息化发展水平进行聚类量化和评估，以期找出各省域、直辖市信息化发展的差距所在，为实现我国信息化水平的均衡发展提供必要参考。

对信息化发展水平的研究是一个涉及多方面的复杂问题，单一指标评价已经不能满足研究的需要。本文结合文献［4］，遵循科学性、综合性、可操作性、可比性原则建立区域信息化水平的指标体系 (见表1)，并通过《中国统计年鉴》、《中国信息年鉴》《中国高新技术发展报告》等年鉴定和统计公报，收集并整理2008年我国大陆各省市信息化发展水平的原始数据，运用SPSS17．0统计软件对我国各省市信息化发展水平进行聚类量化和评估。

表1 信息化建设水平指标体系

二、基于因子分析进行聚类分析的理论依据

因子分析主要用于对数据进行降维与简化处理，侧重于研究众多变量间的相互依存关系，并从中抽象出潜在变量，即“因子”来反映原来众多变量的主要信息。在对事物总体的研究中，设在p个变量x1，x2，…，xp中抽取一个样本，组成相关系数矩阵X= (xi1，xi2，…，xip)，i=1，2，…，n，其中所包含的指标复杂多样，往往难以对所研究事物进行合理解释和正确评价。因而通过因子分析，将所研究变量表示为公共因子的线性函数，即 X=AF，其中 A= (A1，A2，…，Ap)为因子载荷矩阵，F为公共因子，以F代替X，由于n＜p，从而达到简化变量维数的目的。首先，对随机向量X= (x1，x2，…，xp)进行标准化处理，并估计因子载荷矩阵A=(A1，x2，…，xp)，设随机向量X= (x1，x2，…，xp)的协方差矩阵为Σ，因而R=Σ，λ1≥λ2≥…≥λp为Σ的特征向量，v1，v2，…，vp为对应的标准正交化向量，为了使变换前后空间中两点距离保持不变，要满足…，p)，λ1是矩阵R的特征值，一般选前k个特征值所对应的因子载荷矩阵A的前k个列向量组成的矩阵作为因子载荷矩阵，只要使累计贡献率达到85%以上。即。这样确定k之后，所抽取的因子变量的数量远少于原有指标变量的数量，并能够反映原有众多指标的绝大部分信息。

在因子分析的基础上，利用系统聚类法将相近的样品先聚成类，类间距离定义采取中间距离法，利用中间距离法将类Gp和Gq合并为Gr，则任意类Gk和Gk的距离公式，聚类结果可直观反映在系统谱系图中。

三、用SPSS进行基于因子分析的聚类实证过程和结果

(一)用SPSS进行因子分析的过程与结果

利用SPSS17．0统计软件对全国28个省及直辖市 (西藏、青海和新疆数据缺失，因而作为缺省值处理)的信息化发展水平进行因子分析。首先，SPSS17．0统计软件对原始数据变量自动进行了标准化处理，消除了变量间的量级影响，其后计算样本协方差矩阵S= (rij)28×14。求解载荷矩阵，将特征根的大小依次排序;并结合的贡献率和累积贡献率抽取公因子。

在运用因子分析方法之前，需对样本进行适合性检验，一般而言KMO的取值在0和1之间，KMO越接近于1，则越适合作因子分析的标准，软件分析结果显示Bartlett球体检验的显著概率为0．000，KMO检验值为0．730。由此可认为文中所选择的指标适合进行因子分析。根据输出结果(见表2)，有3个公因子的特征值大于1，这3个公因子可以解释90．59%的方差，可以认为这3个因子基本反映了原变量的绝大部分信息。由此用3个主因子代替原来的14个指标，既减少了变量维数，又消除了指标间相关性。

表2 方差贡献分析表

通过表3的因子得分系数矩阵，主成份表达式可以用各原始变量写出：成份1=0．167C1-0．104C2-0．102C3+0．128C4+0．163C5+0．111C6+0．000C7+0．134C8+0．136C9+0．107C10+0．060C11-0．036C12+0．150C13+0．058C14; 成份2和成份3可以依次得到。

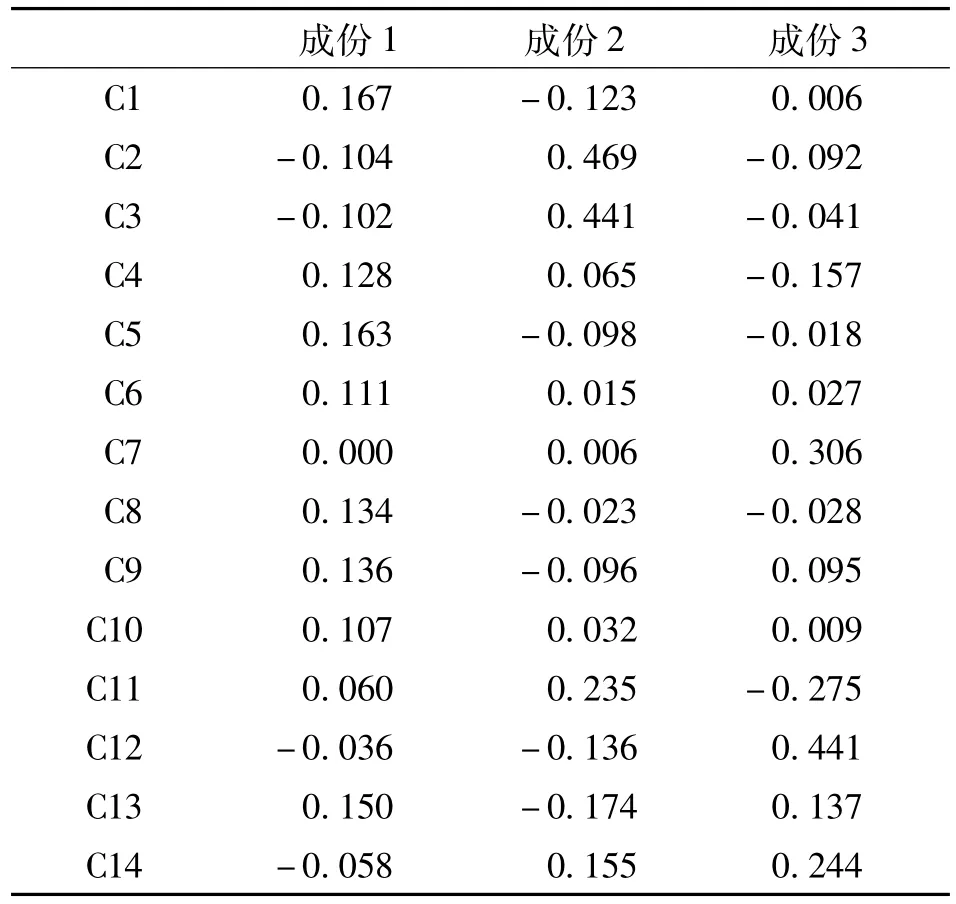
表3 因子得分系数矩阵

为了对各省信息化发展的整体水平有一个明确的综合性的评价，进一步以主因子值旋转平方和载入的方差贡献率为权重，计算各省信息化发展水平的整体综合得分。如表2所示，第一主因子的权重为0．534，第二主因子的权重为0．19。第三主因子的权重为0．181。

表4 各省市信息化发展水平的因子得分系数及综合得分

(续表4)

从表4中可以看出，广东综合得分领先于其他省市，信息化发展水平最高;北京、上海、江苏、浙江和山东的信息化发展水平位居全国前列。而甘肃、内蒙古、贵州、云南、海南、宁夏等省的信息化建设缓慢，发展水平较低，其他省份的信息化发展水平在国内则处于中等水平。

(二)在因子分析基础上的聚类过程

在因子分析中产生的新的3个公因子及其综合得分的基础上，运用系统聚类方法对28个省市(西藏、青海和新疆数据缺失，作为缺省值处理)信息化发展水平的聚类。

如图1所示，可以看出各地区的信息化发展水平基本分为4类：第一类仅包括广东省，其信息化发展水平及综合得分遥遥领先;第二类包括北京、天津、上海、江苏、浙江和山东;第四类包括内蒙古、海南、贵州、云南、甘肃、宁夏。其余都属于第三类地区。

四、结果分析及建议

在因子分析基础上的聚类结果表明，第一类广东，信息化发展水平最高;第二类地区包括上海、北京、天津、浙江、江苏和山东，结合表4的信息化发展水平综合得分，也验证了这五个省市信息化发展水平突出。第四类是内蒙古、海南、贵州、云南、甘肃和宁夏，其信息化发展水平综合得分较后，说明这些省市信息化发展水平相对最落后。可以看出，我国东中西部地区的信息化建设发展水平区域差异巨大，基本上形成了东中部地区与西部地区发展明显差距。其中广东省信息化建设发展较快，远远领先于其他省市，而上海、北京、天津、浙江和江苏等省市发展水平也较高，形成长江三角洲和京津地区两大经济区域优先发展的态势;而西部地区省份，如宁夏、甘肃、云南和贵州等省份相对发展水平缓慢，以上分类情况与现实中东中经济区划中各省实际水平基本相符。

广东、上海、北京、浙江、江苏等省市是我国改革开放以来最先发展起来的地区，具有强大的经济基础、科技与人文等方面的突出优势，为信息化建设提供了强有力的支撑。广东地处地珠江三角洲，最易获得先进技术和信息，改革开放后外向型经济蓬勃发展，具有信息化建设雄厚的财力和技术支持;而北京、上海、浙江、江苏等省经济繁荣，人文荟萃，地处京津塘、长江三角洲地区，集中了我国大量的优秀企业和各类人才，信息化建设优势也较为明显。而在此基础上，以上省份应充分发挥优势，强化信息高新技术产品的工业化生产与开拓，保持信息化与工业化建设的较高水平，形成较强的聚集效应和创新优势。同时发挥辐射作用，通过加强与中西部地区的信息化技术合作与交流，带动中西部地区实现信息化的跨越式发展。

反观内蒙古、海南、贵州、云南、甘肃和宁夏等省份，由于经济基础薄弱，地处偏远，交通不便等因素的影响，信息化建设水平较低，在今后的发展中政府应注重基础设施建设，加大教育投入，通过税收、财政一系列优惠政策积极促进发展滞后省份的信息化建设，同时加强信息化技术交流，合理配置资源，力争缩小区域信息化差距，实现区域均衡协调发展。

［1］张明军．我国各地区信息化水平的综合评价［J］．学术纵横，2009(5)：103-104．

［2］王梅英．信息化对区域经济影响的数理分析［J］．数理统计与管理，2004，26(3)：41-44．

［3］吴迎春．基于因子分析的地区信息化水平实证研究［J］．中国科技产业，2009(3)：121-122．

［4］杨京英，闾海琪．2006年中外信息化发展指数测算与比较研究［M］．中国信息年鉴，2007：421-427．

［5］陈爽英，唐小我．基于因子分析的中国城市循环经济发展水平的聚类研究［J］．管理工程学报，2008，22(4)：155-158．

［6］朱建平．应用多元统计分析［M］．北京：科学出版社，2006．

［7］张勇刚．企业信息化测度理论与方法研究［J］．科研管理，2006，27(1)：107-113．

［8］汪莹．企业信息化的效应理论与评价方法研究［M］．北京：中国经济出版社，2006．

［9］司有和．企业信息管理学 ［M］．北京：科学出版社，2003．

［10］王众托．信息化与管理变革［J］．管理科学学报，2000(6)：1-8．