锚杆参数优化在开挖边坡加固中的应用研究

张良发

(湖北省宜昌地质勘探大队，湖北宜昌 443100)

锚杆参数优化在开挖边坡加固中的应用研究

张良发

(湖北省宜昌地质勘探大队，湖北宜昌 443100)

结合工程实例，采用有限差分法建立数值模型。分别改变锚杆的几个支护参数，利用FLAC软件计算边坡的安全系数，以此分析这些参数对于边坡稳定性的影响，从而选择合适的参数。运用数学方法和有限差分法，对支护前和支护后的边坡进行稳定性分析，通过监测结果验证了锚杆参数选择的合理性。

边坡支护;锚杆参数;边坡稳定性;安全系数

0 引言

锚杆支护是近年发展起来的用于岩土工程的一种挡土技术，具有施工简单、加固效果显著和造价低等优点，适用于深基坑工程和边坡支护工程，它较多地用作开挖边坡的临时支护，也可作为永久性挡土结构［1］。然而，在目前的实际工程中，人们对锚杆支护参数基本是凭借工程经验进行选取，不能合理有效地进行设计，这给工程带来一定隐患，也会造成工程材料的极大浪费。因此，有必要进一步研究合理的支护参数，正确指导设计和施工，确保边坡稳定性和合理的施工成本［2］。随着计算方法和各种数值模拟技术在岩土工程中的不断发展，本文应用了有限差分法模拟锚杆的支护效果，定量得出了各个支护参数与边坡稳定性的关系，从而确定锚杆支护最优参数。

1 工程概况

1.1 场地条件

某工业开发区工程，因修建工业大楼的需要，拟将其旁一山体内侧的岩土体挖掉。开挖后将形成土—岩混合边坡，边坡安全等级为二级。被开挖部分山体的垂直高度为15.5 m，按1∶0.4的比例分两次放坡，放坡高度分别为8 m和7.5 m。

由于山体开挖后的边坡稳定性将直接影响建筑物的安全使用，故需根据该山体的地质情况正确分析其开挖后所形成边坡的稳定性，制定合理的边坡支护方案。

1.2 工程地质条件

根据岩土工程勘察报告显示，该山体内的地层自上而下的顺序主要有：第四系坡洪积层、冲洪积层、残积层以及侏罗系中统基岩，其岩土体的物理力学参数如表1所示。

由边坡的工程条件可知，边坡主要为第四系冲洪积层和第四系坡残积层，其土层抗剪强度较大，但局部破碎、软硬互层的构造特性又导致其稳定性较低，在地表水及雨水作用下边坡容易发生滑塌。边坡开挖之后，在坡体内发现一个顺坡向的软弱结构面，倾角约30°，长度约25 m，倾角小于坡角，对边坡的稳定性构成潜在的严重威胁。在滑体后部产生张裂缝，裂隙深为5 m，裂隙内水深4 m。该张裂缝对边坡的稳定性有很大的影响，特别是在暴雨情况下，由于张裂缝底部排水不畅，张裂缝可能临时充水达一定高度，沿张裂缝及滑动面产生静水压力，使滑动力突然增大，造成边坡滑移［3］。

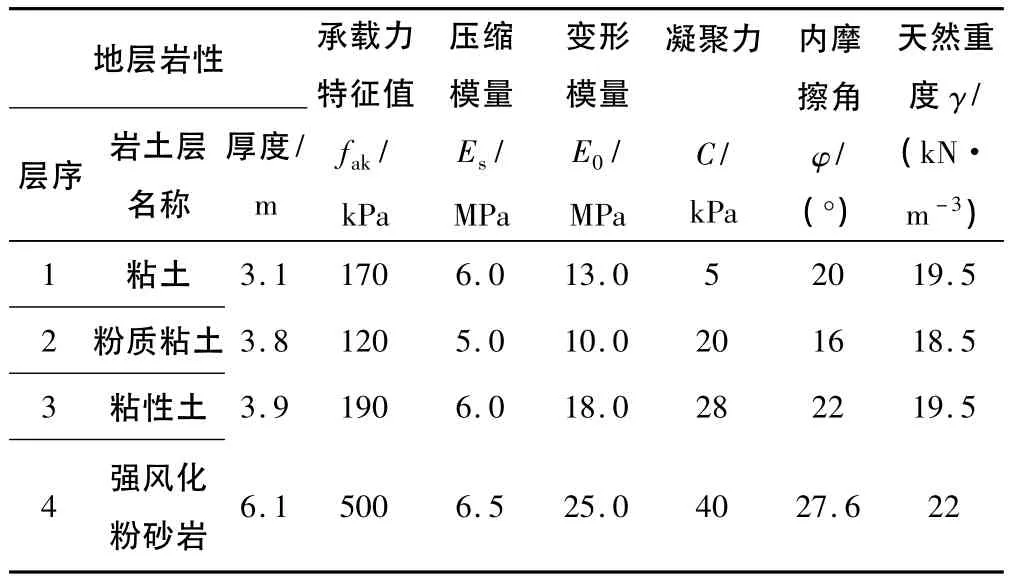
表1 岩土层的物理力学指标一览表Table 1 Geotechnical layer of the physical and mechanical indexes list

2 稳定性分析

将边坡假设为均质边坡，则边坡的稳定性分析可按平面剪切破坏类型考虑，见图1。

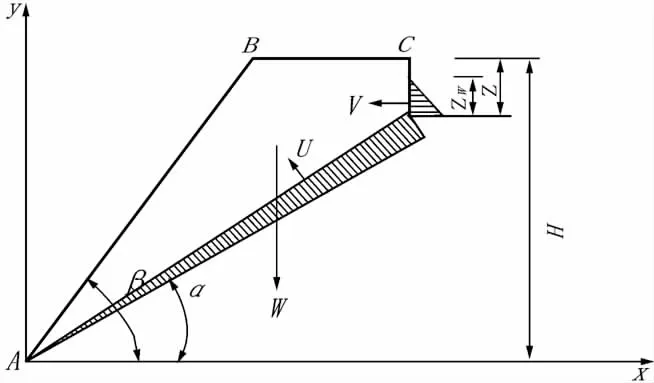
图1 具有张裂隙和静水压力的边坡Fig.1 Slope with tension joint and water pressure

用刚性极限平衡法分析，稳定系数可按下列公式计算：

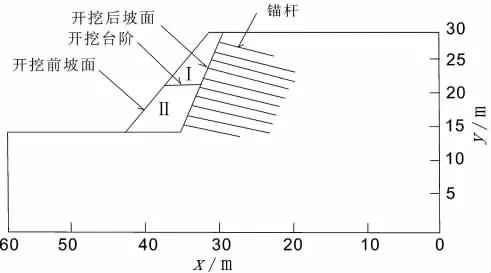
图2 边坡计算模型示意图Fig.2 Figure of calculation model for slope

根据上述几何模型及计算参数，编写FLAC计算程序，并运行FLAC软件作数值模拟分析，对模型边坡进行网格划分。最后开挖完成的有限差分网格如图3所示。

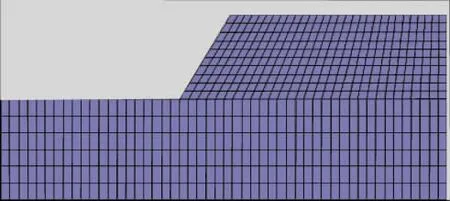
图3 开挖边坡网格图Fig.3 Excavated slope trellis

式中：L为滑动面长度(m);β为边坡坡脚(°);α为滑动面倾角(°);u为作用在滑块地面上的水浮托力(kPa);v为张拉裂缝中的水压力(kPa);γw为岩体的重度(kN/m3);Z为张裂隙深度(m);Zw为裂隙中水的深度;W为滑体自重(kN)。

c，φ，γ的取值是根据山坡原状岩土试样进行试验得出的。将相应参数代入公式计算得Fs=0.97，小于设计要求的安全系数1.25，不符合规范要求，说明现有边坡稳定性较差，需采取加固措施。

由于边坡空间位置较特殊，坡脚靠工业大楼基础很近，工业楼下设有地下停车库，因此决定采用锚杆支护。

3 锚杆参数优化设计

对于纵向较长的实体边坡，其计算模型可以简化为平面应变问题［4］。

本模型计算范围选取：H=30 m，L=60 m;模型的边界条件为：两侧边界约束水平位移为0，下侧边界约束竖向位移为0。其计算模型剖面示意图为图2所示。

为了选取合适的锚杆参数，这里采用单因素分析方法研究锚杆长度(L)、锚杆倾角(α)、锚杆垂直间距(V)等支护参数对边坡稳定性的影响，即：选定1个基准模型，变化其中的1个参数，通过数值模拟计算边坡安全系数，并进行分析，选出锚杆支护参数的最优化方案［5］。

3.1 锚杆长度的选择

根据设计规范可将锚杆倾角固定为15°，选取网格面积(长×宽)为2 m×2 m，L每次递增2 m。代入相关物理参数，分析L从2～20m递增过程中，K随锚杆长度的变化情况，结果如图4所示。

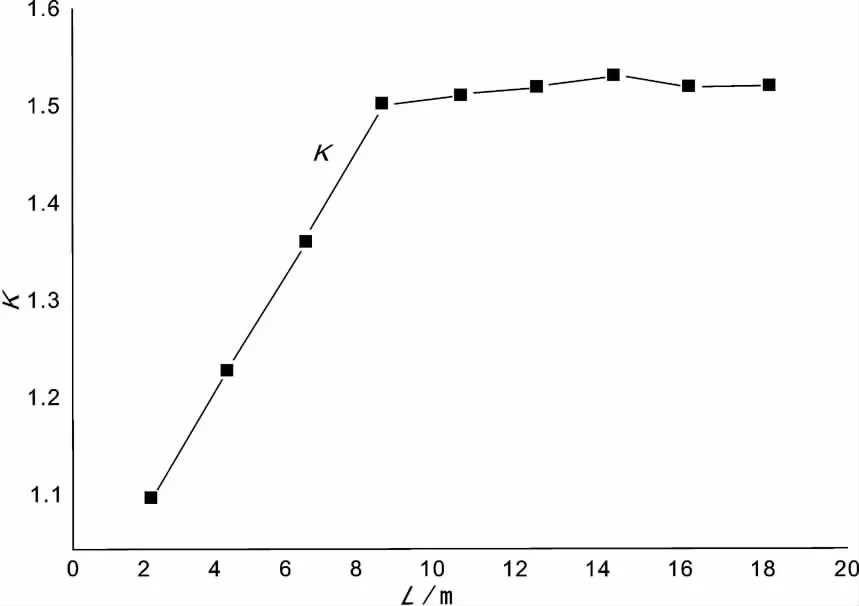
图4 L与K的关系Fig.4 The relation between L and K

由图4可知，当锚杆长度达到某一数值后，再增加其长度，边坡稳定性系数基本上没有大的变化。可见L增加到一定长度后并不能提高边坡的安全系数。在L=10～14 m时，K值较大。根据边坡稳定性和锚杆的经济性，选取锚杆长度为8～12 m为宜。

3.2 锚杆倾角的选择

为了分析锚杆倾角对边坡安全系数的影响，将锚杆长度固定为12 m，网格面积(长×宽)为2 m×2 m，α每次递增5°。得到K随锚杆倾角的变化情况，结果如图5所示。

图5 α与K的关系Fig.5 The relation between α and K

由图5可知，在α从水平方向逐渐增大的过程中，K先增大然后减小。当α较小时，K达到最大值;继续增加α，K逐渐减小，减小的趋势基本是呈线性的。可见，锚杆倾角为5°～15°时，边坡稳定性较好。锚固角的计算公式δ=45°+φ/2－α，根据最大抗滑力锚固角和最经济锚固角确定锚杆的最优化锚固角。选取锚杆钻孔与水平方向的夹角为15°。

3.3 锚杆垂直间距的选择

在每个边坡模型中加入5根锚杆，锚杆倾角为15°，长度为12 m，从离坡顶0.5 m处布置第1根锚杆，垂直间距为0.5～3.5 m。得到K随锚杆间距的变化情况，结果如图6所示。

图6 锚杆间距与K的关系Fig.6 The relation between V and K

由图6可知，K随着锚杆间距的增大而增大，当锚杆间距达到一定值时，K又随着锚杆间距的增大而减小。在V=3 m时，K取得最大值。故锚杆间距为3 m时，边坡稳定性相对较好。

3.4 锚杆材料的选择

锚杆拉力公式为：

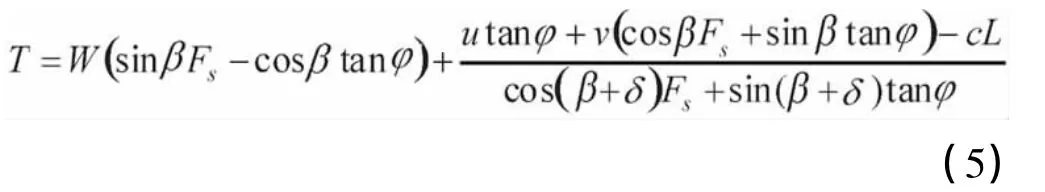
式中：δ为锚杆与水平面夹角，其余符号与前相同。根据《岩土工程勘察规范》(GB50021—94)，Fs取 1.25计算，得锚杆拉力T=520 kN/m。公式：

其中Nt=Ti，m，n分别为锚杆间距和排数［6］。经计算得出：单根锚杆抗拔力设计值Nt=130 kN。有锚杆抗拉验算公式：

式中：K为安全系数;Nt为锚杆设计轴向力;As为锚筋截面积;fpkt为锚筋(钢筋)抗拉强度设计值为455 N/mm2。

经计算，锚杆As=457 mm2，一条25的Ⅱ级螺纹钢筋截面积为490 mm2＞As，满足要求。

3.5 锚杆支护参数选取

采用锚杆支护的方案，可有效控制边坡土体变形，以确保边坡稳定，满足边坡安全的要求。根据锚杆支护的合理性和经济型，选取锚杆支护参数为：长度L=12 m、倾角 α =15°、间距V=3 m、直径D=25 mm。

4 支护后边坡稳定性分析及监测

4.1 安全系数分析

边坡支护后对其稳定性进行了分析，计算按照平面应变问题处理，土体用平面单元plane2模拟，锚杆用梁单元beam3单元模拟。模型计算范围为60 m(长)×30 m(高)，边界条件：左右两侧水平约束，下部竖向约束，上部边界为自由边界［7］。屈服准则：采用Drucker－prager屈服准则。钢筋弹性模量2.0×105MPa，抗拉强度310 MPa。用拉格朗日差分法进行数值分析，模型中加上锚杆时，输入相关参数进行计算得安全系数K=1.4。K＞1.25，故支护后的边坡是稳定的。

4.2 边坡监测

该边坡支护工程施工结束后对边坡进行了监测。边坡监测采用位移监测，选取了3个位置重要点进行监测，其中1、3号点位于边坡两侧坡腰，2号点位于坡顶。其监测数据如表2(单位mm)。

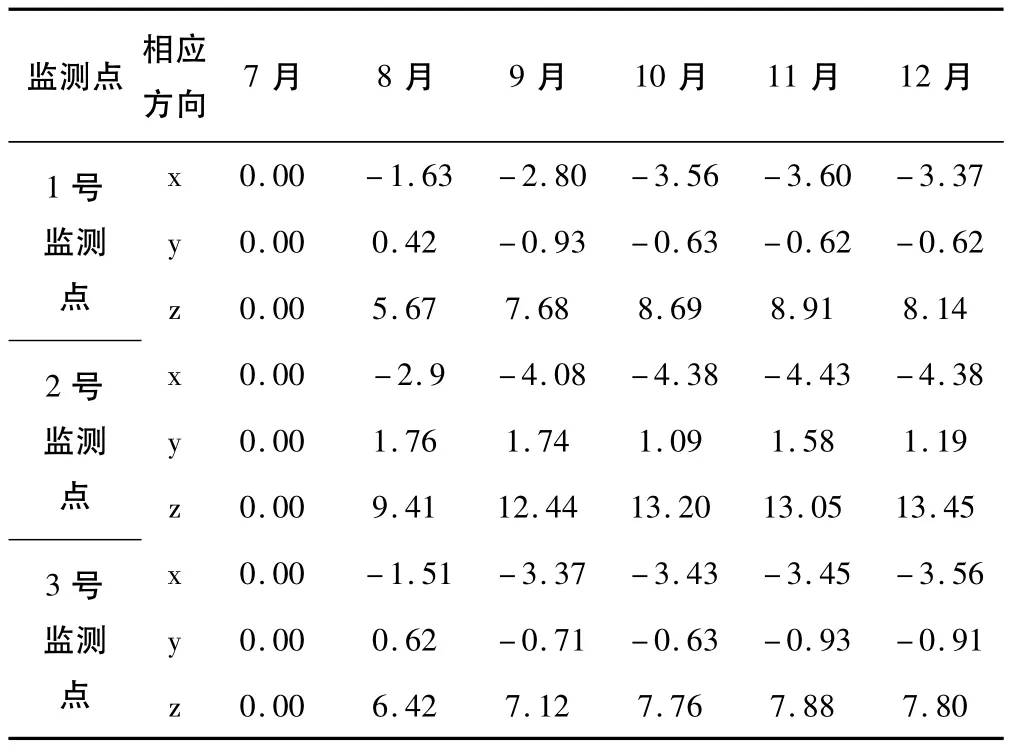
表2 位移监测数据Table 2 Displacement monitoring data

3个监测点的位移沉降量如图7所示。

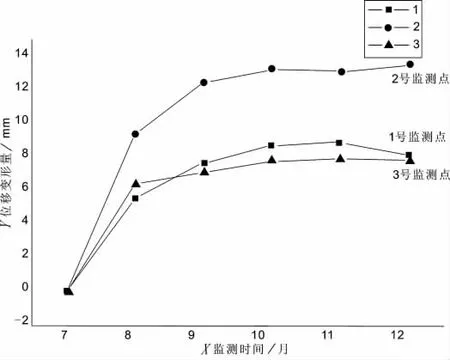
图7 监测点位移沉降量Fig.7 Displacement settlement monitoring points

经连续的位移和沉降观测，由监测数据和沉降量变化曲线可知，该边坡支护后位移和沉降变化量较小，边坡稳定性较高。

5 结语

本文通过工程实例，运用有限差分数值分析法分析了不同锚杆支护参数对边坡稳定性的影响，得出锚杆的最优支护参数。通过对边坡支护前后稳定性的分析，证明了这种方案的可行性。可见通过优化设计选取合适锚杆长度、倾角、间距和直径等参数不仅能提高边坡稳定性，而且节约了工程材料、降低了施工成本，取得了显著的经济和社会效益，在边坡支护中可推广应用［8］。

［1］中国岩土锚固工程协会.岩土锚固新技术［M］.北京：人民交通出版社，1998.

［2］陈强.预应力锚杆在基坑支护工程中的应用［J］.西部探矿工程，2003(1)：13 －14.

［3］ 林宗元.岩土工程治理手册［M］.沈阳：辽宁科学技术出版社，1993.

［4］郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，23(19)：3 381－3 388.

［5］彭文祥，赵明华，等.基于拉格朗日差分法的全长注浆锚杆支护参数优化［J］.中南大学学报，2006，37(5)：1 002 －1 007.

［6］中国工程建设标准协会.土层锚杆设计与施工规范［S］.北京：中国建筑工业出版社，1990.

［7］朱宗明.FLAC在边坡整治工程中的应用［J］.广州建筑，2003(4)：40－42.

［8］中国岩土锚固工程协会.岩土锚固工程技术［M］.北京：人民交通出版社，1996.

Application of Parameter Optimization of Anchor Bolt on Slope Reinforcement during Excavation

ZHANG Liangfa
(Yichang Brigade of Geological Exploration in Hubei Province，Yichang，Hubei443100)

With an engineering example，the numerical models were founded by the finite－ difference method.Using FLAC for calculating on the safety factors of the slope，each support parameter of anchor bolts is changed，the influence of the parameters is analyzed in order to choose the appropriate ones.Then the mathematical methods and finitedifference method are adopted to study the slope stability before and after the support.The results of monitoring show that the parameter determination is rationality.

slope support;parameters of anchor bolts;slope stability;safety factor

TU753.8

A

1671－1211(2011)03－0248－04

2011－03－31;改回日期：2011－05－24

张良发 (1969－)，男，高级工程师，地质技术经济专业，从事水文地质、工程地质、环境地质勘查设计及技术质量管理工作。E － mail：172646987@qq.com

潘 潇)