一种新型有限元网格形状评价指标

张 吉 陈岱林 王 徽 梁 博

(中国建筑科学研究院建筑工程软件研究所,北京 100013)

一种新型有限元网格形状评价指标

张 吉 陈岱林 王 徽 梁 博

(中国建筑科学研究院建筑工程软件研究所,北京 100013)

本文对通用有限元软件ANSYS与 SAP2000中的单个网格评价指标进行了分析与总结。在现有单个网格评价指标计算的基础上,建议了一种新的网格评价指标,该评价指标不仅能用于单个网格的评价,而且能用于复杂的多网格有限元模型。通过 C++编程实现了整个评价指标的计算,对悬臂梁模型采用不同网格划分后对形状指标进行计算后,发现按不同网格的形状指标与计算精确度存在明显的正相关性。将其用于多高层建筑结构网格评价,计算结果表明该评价指标是高效而又可靠的。

网格;有限单元法;形状指数

1 概述

一般说来,单元和网格性能同时影响有限元数值计算结果的精度。一方面,性能好的单元,在粗糙的或畸形的网格下都能求解出理想的场变量,场变量包括受轴力下的轴向变形、受剪结构中剪应变(应力)、受弯构件中的拉、压应变 (应力)等。例如,在经典四结点双线性位移场 Q4单元基础上增加含内参的附加位移场构造的非协调位移元Q6单元,在单元形状规则或者畸变的情况下,性能都比只具有双线性位移形函数的Q4单元的数值计算结果要好[1]。相反,良好的网格划分能减低对单元性能的要求。不只是精度与网格有关,常用于考核单元性能的小片检验也与网格有关,有些非协调单元在矩形形状下就能通过小片试验,而在非矩形的形状下就不能通过[2]。

文献[6,7]中对映射法、基于栅格法等网格划分方式进行了详细的介绍,关于网格划分更进一步的研究是基于几何形状的自适应网格划分技术[3-5],几何自适应网格能识别所分析区域的外形,在场变量梯度可能大的区域自动加密网格。但几何自适应网格划分过程过于复杂,且与所加荷载形式相关,目前工程中应用不多,而广泛采用的是指定一个整体网格控制尺寸,对区域进行均匀划分。不论何种网格方式,都不能保证在一定的控制尺寸下,网格是最优的,尤其是针对高层建筑等复杂结构的网格划分形状。因此,本文所研究的问题是,使用相同的单元,在相当的求解消耗下,对网格形状优劣进行评价;并得出一个定量的指标,以描述单元形状对数值计算结果的影响程度。

2 单网格形状评价指标

当前流行的通用有限元软件 ANSYS与SAP2000中都具有强大的自动网格划分功能,并且依据不同标准给出每个单元形状好坏,在ANSYS中还能以图形或者文本方式查看形状差单元的位置与指标值。

2.1 ANSYS中的网格评价指标

(1)长宽比(aspect ratio)指标

如单元具有矩形形状,直接采取长边与短边比值作为长宽比的值,当比值大于 20时,给出警告;当比值达到 106时,给出错误提示。对于任意四边形(如图 1),其长宽比的值,通过以下步骤计算获得:

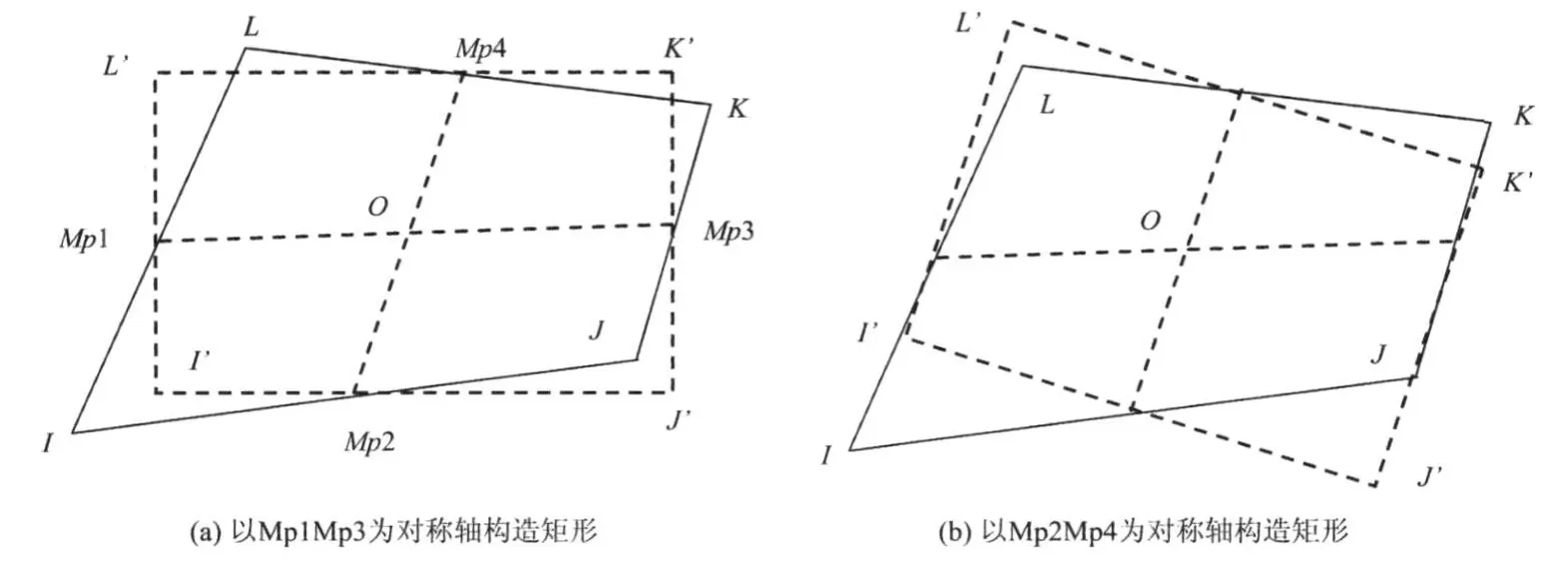
图 1 任意四边形单元长宽比计算简图

¹ 找出四边形四条边的中点Mp1、Mp2、Mp3和Mp4,分别连接两对边中点形成两条中线Mp1 Mp3,Mp2 Mp4;

④以其中任意的中线为对称轴线,绘制一矩形I'J'K'L',并且使矩形的各边均通过原四边形的中点;

㈣以新绘成两个矩形的 I'J'K'L'长边与短边之比值的较大值作为原四边形的长宽比。

此法每步计算的实现均需要较大的运算量;而且,当原四边形为等腰梯形,且梯形高度与两腰线中点连线长度相等时,计算的长宽比值为 1,即该指标有可能将其误判为正方形。

(2)平行偏离(parallel deviation)指标

用于评价两对边偏离平行线的程度,即偏离矩形的程度。对图 2中梯形,通过以下方式计算:

¹先求各边所在直线的单位向量 v1,v2,v3和v4,再求两对边单位向量的点积;

④从向量代数可知,该点积结果即为两对边夹角余弦值,故可找出两点积中的较大值,通过反余弦求出其夹角以反映网格偏离矩形的程度。当夹角为 0°时,两对边平行,当夹角变大时,其偏离程度越高,性能也会越差。

对于不含边中节点的四节点单元,ANSYS默认设置为夹角达 70°时给出警告,150°时给出错误提示。

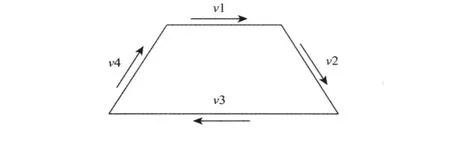
图 2 平行偏离指标计算简图

(3)雅克比比例法(Jacobian Ratios)

雅克比,即为将任意形状单元从物理坐标中转往基准坐标系的基准单元时,采用的变换矩阵的行列式。当物理坐标系中的原始单元为非矩形形状时,行列式值为一变量,该变量随着基准坐标值的变化而不断改变,因而在同一个原始单元中的四个角结点处,雅克比有不同的值。雅克比比例取定为所有四个结点中雅克比的最大值与最小值的比值。不难理解,该比值越大,隐含了该坐标变换可能带来越大计算隐患,数值计算结果的可靠性也就越低。

但是物理单元的形状为矩形或者平行四边形时,雅克比为一常数,且等于A/4,A为矩形母单元面积,此时该法则将失效。

2.2 SAP2000中的网格评价指标

长宽比指标

对于任意的四边形时网格,建议了两种计算方法,第一种计算方法如图 3(a)所示。并指出,在关注分析问题的应力时,长宽比不应超过小于 1/3,当关注分析问题的位移场为主时,长宽比不应小于 1/5。

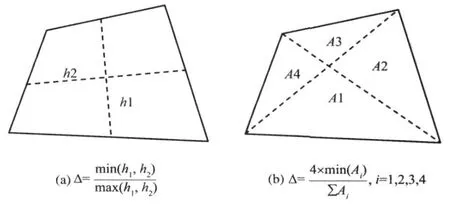
图 3 SAP2000中第一类网格评价指标计算简图

第二种计算方法如图 3(b)中所示,其中 A1,A2,A3,A4为四边形对角线剖分成的四个小三角形的面积。

除要求单元长宽比之外,还要求四边形的所有内角应在 45°到 135°之间;然而,SAP2000提供的第一类计算方式也存在 ANSYS中长宽比计算时相同的不足;第二类计算方法,当四边形单元为矩形时,不论矩形形状如何狭长,其评价指标保持为一恒定值1。

3 本文建议的网格形状评价指数

采用上面介绍的通用有限元软件提供的评价指标在某些情况下具有一定的局限性,通常在对某一种形状网格判定时,能取得较好的效果,而应用于另外形状时,则不甚理想;因此对单元形状进行评价时,往往需要同时考虑多个指标,如长宽比,大钝角,尖锐角等的综合影响;而且,对于建筑结构而言,关注的问题不是某一个单元的性态或某一点的应力,而是结构的位移及内力等整体层面的物理量,因而能够对整个结构网格好坏评价的指标将更有实用意义。基于上述原因,本文从在学习以上一些做法的优点基础上,提出了如下可行的且易于编程实现的一种网格评价指标。该评价指标既能处理网格全部为四边形单元情况,也能处理网格同时包含四边形与三角形单元的情况:

3.1 四边形网格的计算方法

主要计算步骤如下:

(1)连接任意四边形的两对角点形成两对角线,两对角线将四边形分成 4个小三角形(如图 4);

(2)分别求出 △AOB、△ BOD、△DOC、△COA周长,并找出最大值,最小值;

(3)以第(2)步中求出的周长最小的三角形的周长与最大周长三角形的周长的比值;

(4)找出对角线交点与四个角节点所连线段长度的最小值与最大值,计算最小值与最大值的比值乘到第(3)步计算的结果上,即为该四边形最终的形状参考指数。

为后文陈述方便,不妨命名该形状指数为 irreg_ratio,该指数的计算式可写成1m2,其中:

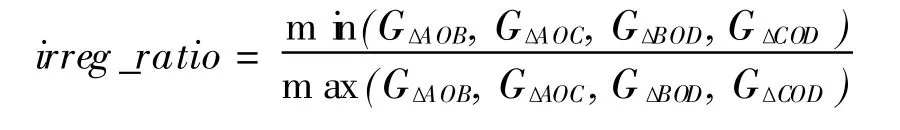
a)为正方形,边长为 1m;

b)为平行四变形,底边长 1m,侧边长m;

c)为矩形,宽 0.5m,高 2m;

d)为等腰矩形,下底宽 1.5m,上底宽 0.5m。

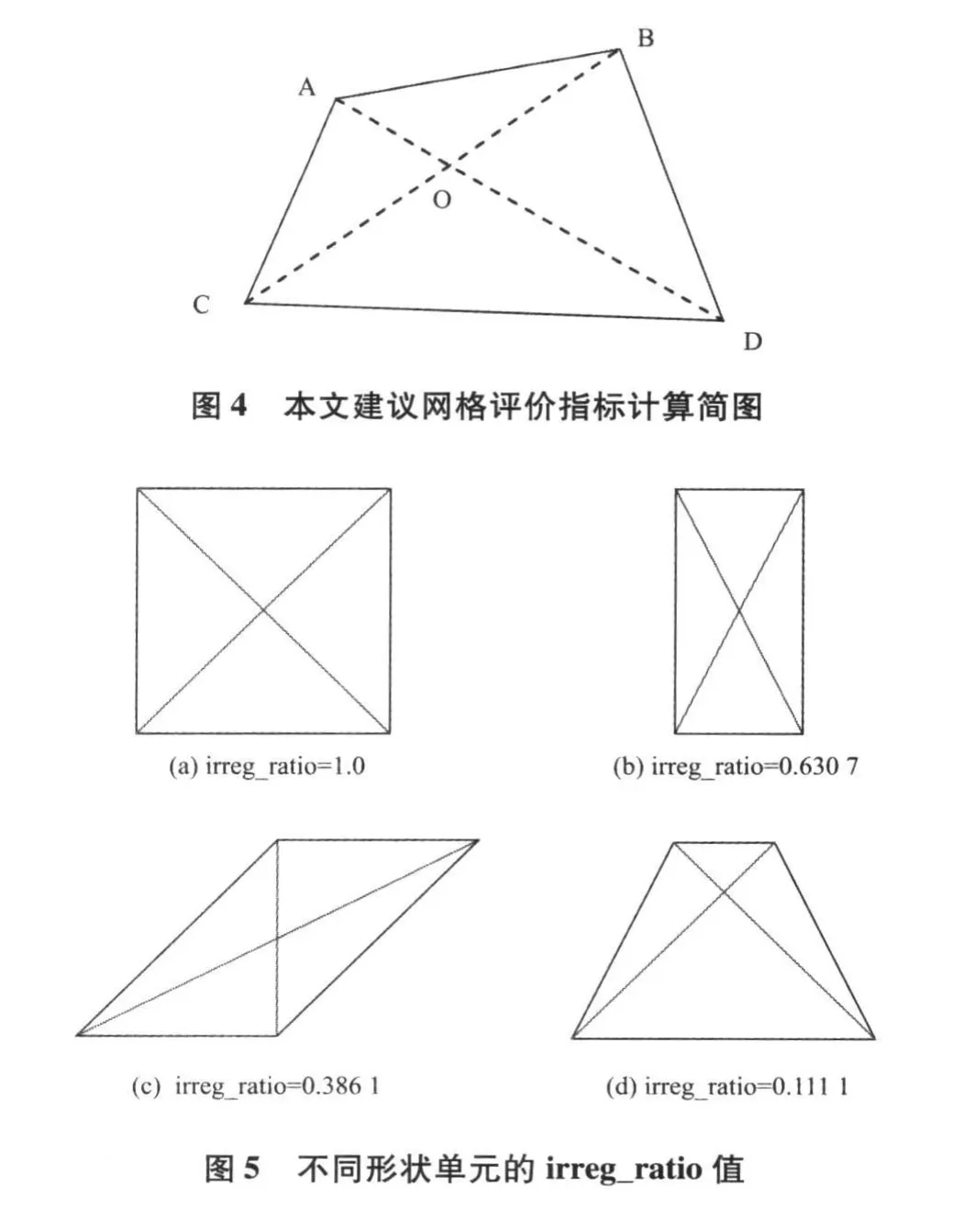
为了初步考证该指数的性能,即指数大小与单元形状好坏之间的相关性,对图 5中一组单元的形状指数进行计算,所有单元的面积都是相同的,即

初步看来,该指标具有以下一些优点:

a)计算简洁,只需简单的几何运算即能求解;

b)能同时反映边长比偏离 1与小锐角与大钝角的程度,当单元形状为正方形时,即最佳网格时,irreg_ratio=1;

c)从 1到 4网格,rreg_ratio偏离 1越来越大,其值越来越小,单元性能也将越差,与数值计算结论相符[8]的,也说明了该指标的合理性;

整个结构只划分成一个单元情况是非常少见的。而在多个单元组成的分析区域中,存在极个别的形状差的单元对计算效果影响是比较微小的,作者已做过类似的数值试验。因此,为了将该形状指数应用于多网格分析域的网格评价,在单个单元形状指数的计算方法上再增加以下步骤:

(5)求出每个单元的面积与整个分析域的面积;

(6)遍历每个单元,求出每个单元的形状指数与该单元的面积之积的总和;

(7)将第(6)步求出的值与整个分析域的面积之比,作为整个分析域网格状况的评价指标。

3.2 三角形网格的计算方法

网格划分时,为了降低划分难度,或者提高划分成功率,通过会允许在整体网格中加非常少量的三角形单元。为了适应三角形单元形状的评价,本文建议做法是直接将三角形单元的形状指数置为0。当图 6中四边形角点A不断与 C点靠近时,单元形状将趋于三角形。此时△COA的周长是 4个三角形周长中最小值,并且接近于 0。由形状指数的定义,并且考虑到三角形单元的计算性能,不难理解可将形状指数值取为 0。

基于上述网格指数的计算步骤,作者编制了适合于任意网格形状评价指标计算的 C++程序。计算过程中用到的网格信息均来自于ANSYS软件,在ANSYS中建成几何模型后,调用其网格划分程序自动划分模型,通过简单后处理操作就可将数据文件中网格信息输出到指定文本文件,后续过程所需数据均从该文本文件中读取。

3.3 验证实例

为了进一步验证评价指标用于多单元时的适用性,以MacNeal问题(如图 7)作为分析对象,探索指标值与各种可能的受力条件下的精度关系。详细参数及模型描述可以参考相关文献[8],本文仅做简单描述:通过改变单元侧边与水平面得夹角以调整单元的畸变程度,不论是梯形还是平行四边形,均使夹角分 15°,30°,45°三个阶次偏离,在自由端施加轴力以及向下剪力两种荷载,在约束端采取 6自由度全约束的方式,将计算的结果与解析解的比值列于表 1中。

从表 1中可以看出,对于受轴力的情形,由于变形简单,各种单元形状都基本相同的计算效果,此时计算指数值与精度之间关系并不明显;对于剪弯受力工况情形,形状指数与单元的计算效果具有一致的变化趋势,随着单元形状的畸变程度增加,指数变得越小。计算性能较差的梯形单元,其形状指数相对于相同畸变角度的平行四边形要小,因而验证了本文形状指数的适用性。

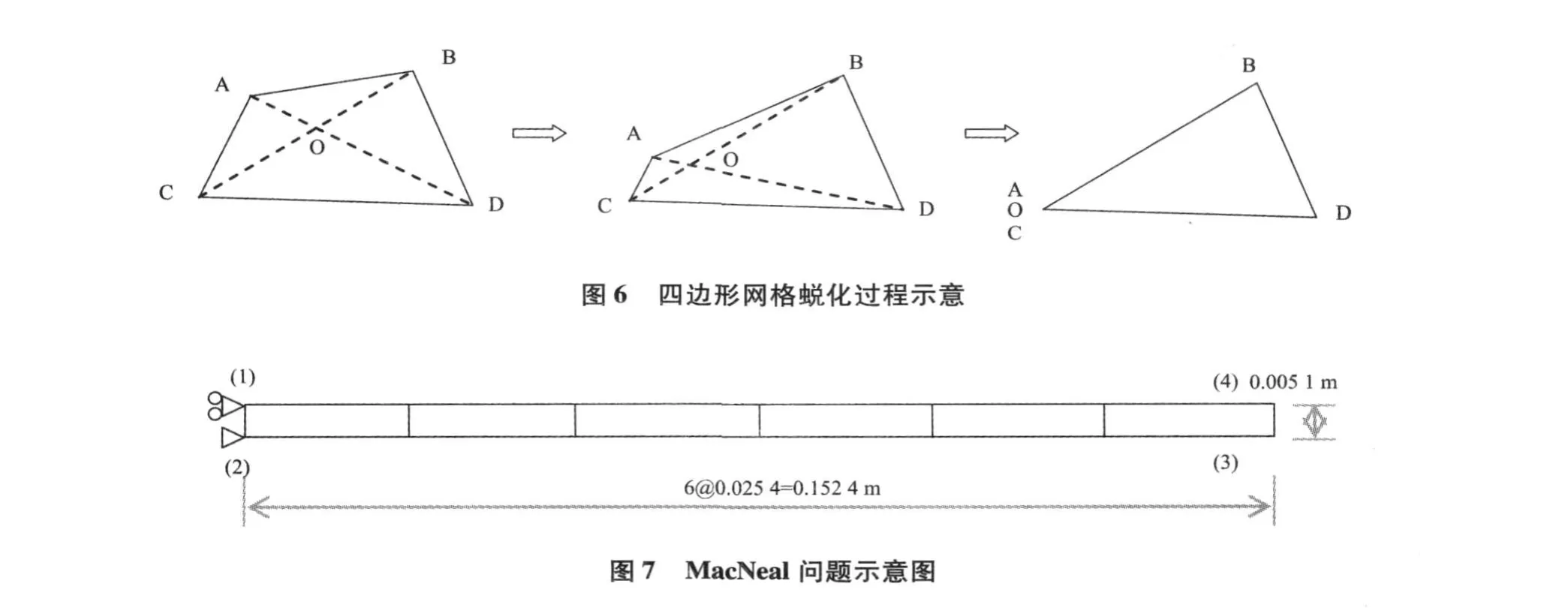
表1 MacNeal问题采用不同形状单元计算的形状指数与求解精度关系

4 结论

本文对结构有限元分析中一个重要的影响因素——网格剖分方案进行一些探讨,通过对比试验及数值算例分析,得出了如下一些结论:本文建议的网格形状评价的指数,计算过程比较简便,既适用于单个网格,也能适用于多网格区域的网格性能评价。将该指标推广到多高层建筑结构网格评价后,计算表明该指标仍然高效可靠。

[1]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.

[2]ROBERT D Cook,DAVID SMalkus,MI CHAEL E Plesha,et a.l Concepts and applications of finite ele ment analysis[M].4th ed.Ne w York:JohnWiley&Sons,2001.

[3]黄晓东,杜群贵,叶邦彦.二维几何特征自适应有限元网格生成(一)——几何特征识别[J].计算机辅助设计与图形学学报,2004(7):923-928.

[4]杜群贵,刘邵宏,黄晓东.二维几何特征自适应有限元网格生成(二)——算法描述[J].计算机辅助设计与图形学学报,2004(7):929-934.

[5]傅沛福,吴淑芳,胡平等.全自动自适应网格细化[J].计算力学学报,1997(2):114-118.

[6]K Hole.Finite elementmesh generation methods:a review and classification[J].Computer A ided Design, 1988(20):27-38.

[7]关振群,宋超等.有限元网格生成方法研究的新进展[J].计算机辅助设计与图形学报,2003(1):1-14.

[8]R.H.Mac Nea,l R.L.Harder,“A Proposed Standard Set of Proble ms to Test Finite Ele ment Accuracy”,Proceedings,25th SDMFinite Ele mentValidation Forum,1984.

A New Index for Finite ElementMesh Shape Evaluate

Zhang Ji,Chen Dailin,Wang Hui,Liang Bo

(Institution of Building Engineering Sof tware,ChinaA cademy of Building Research,Beijing100013,China)

Single ele m entmesh shape evaluate index ofANSYS and SAP2000 is analyzed and summarized in the present paper.Based on this indexes,a new index is proposed.Benefit from the new index,not only single elementmesh but alsomesh compose ofmore elements can be evaluated.A cantileverbea m problem ism eshed by di-f ferent shape and procedure programmed by C++ language is used to calculate this index of themesh,after compared the solution w ith exact one,a conclusion can be draw that there is a strong correlation be tween the index value and the precision of solution.Multilayer and high-rise buildingsmesh is also evaluated,the results show the index is still efficient and reliable.

Mesh;F inite E le m entMethod;Shape Index

TU375.1

A

1674-7461(2011)02-0016-05

张吉(1982-),男,博士研究生。主要从事建筑结构设计软件的研发及有限元数值分析工作。