世博轴阳光谷整体稳定性分析研究
2011-01-06崔家春
崔家春
(同济大学,上海 200092;上海现代建筑设计(集团)有限公司,上海 200041)
世博轴阳光谷整体稳定性分析研究
崔家春
(同济大学,上海 200092;上海现代建筑设计(集团)有限公司,上海 200041)
2010年上海世博轴屋面体系由索膜结构和6个阳光谷钢结构组成,其中阳光谷为自由曲面单层网壳结构。由于阳光谷体量大、杆件截面尺寸小,具有网壳结构的典型特征,所以其稳定性是设计中关心的关键问题之一。本文对第一号阳光谷进行了整体稳定性分析研究。通过调整不同参数,研究了几何非线性、材料弹塑性及初始几何缺陷对结构整体稳定性的影响。分析结果表明,不同条件下结构的稳定承载力均满足国家相关规范要求;加载至第一个临界荷载时部分构件已经进入塑性,表明结构的失稳破坏后于强度破坏。本文采用的方法和研究内容可为类似工程的分析与设计提供参考。
世博轴;阳光谷;单层网壳;整体稳定;初始缺陷
1 基本理论和方法
在现有的研究论文及专著中,关于结构稳定性方面的资料大都集中在规则网壳结构这一领域。这主要是因为规则网壳结构因其体系简单、造型优美、能跨越较大空间等优点在上个世纪末得到了广泛的应用,其具有整体失稳的特征体现得比较明显,得到了比较广泛的关注[1]。
但是近年来随着新颖建筑造型的出现,不规则网壳结构的应用也越来越多。对于不规则的网壳结构,其稳定性分析方法与规则网壳结构的分析方法相同,可以采用相同的计算理论。所以,可以借用传统的规则网壳结构的稳定性分析方法进行不规则网壳结构的稳定性分析。
稳定性分析的目的是确定结构从稳定的平衡状态变为不稳定的平衡状态时临界荷载及其对应的失稳模态。对于典型的壳体结构,稳定性分析包括两个方面,即线性特征值屈曲分析和考虑非线性的“荷载-位移”全过程跟踪分析。
1.1 线性特征值屈曲分析
特征值屈曲分析用来预测一个理想线性结构的理论屈曲强度。其优点是无需进行复杂的非线性分析即可获得结构的临界荷载和屈曲形状,并可为非线性稳定分析提供可参考的荷载系数。特征值屈曲分析中常用的求解方法有Subspace法和Block Lanczos法。特征值屈曲分析的控制方程为:式中,λ为特征值,即通常意义上的荷载因子;[K0]为结构的弹性刚度矩阵;[Kσ]为应力刚度矩阵;{ψ}为位移向量。特征值屈曲分析通常得出非保守的结果,因此其结果不能直接应用于实际工程。

1.2 非线性稳定分析
因为在加载直至达到极限稳定承载力的过程中,结构通常会发生较大的变形,而且其刚度也会伴随着发生退化现象。因此,完整的稳定性过程分析应该考虑几何非线性的影响。考虑几何非线性的有限元控制方程为:
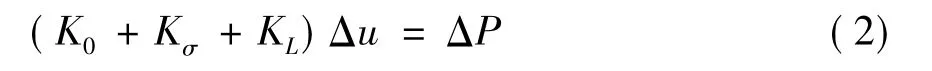
其中,K0、Kσ同上文;KL为大位移刚度矩阵;Δu为位移增量;ΔP为荷载增量。
求解上述方程,即可得到结构在整个加载历史中的“荷载-位移”关系曲线,在非线性稳定分析中应用较多、效果较好的求解方法是弧长法。
另外,由于制造、安装误差等因素,实际结构往往会存在一定的初始几何缺陷,从而与理想结构之间有一定的差异。所以,在非线性稳定分析过程中还要考虑初始几何缺陷的影响,特别是单层网壳等对缺陷敏感型的结构体系。结构的初始几何缺陷一般都是随机分布的,但是在实际分析过程中常采用“一致缺陷模态法”来近似模拟。该方法假定结构的初始缺陷按结构最低阶屈曲模态分布,从理论上也可以证明这是一种统计意义上的最不利分布,因此对每个具有随机分布缺陷的网壳只需进行一次缺陷分析[2]。
2 工程介绍
2010年上海世博轴共有六个不规则的单层曲面网壳结构,称为“阳光谷”。这六个阳光谷形状各异,其中第一号和第六号分别处于世博轴的两端,在体量上最大,所以,本文仅以第一号阳光谷为例,研究这种不规则曲面网壳结构的整体稳定性问题。
第一号阳光谷结构整体形状近似一朵喇叭花。底部为一椭圆形闭合曲线,其中长轴为18.0m,短轴为12.0m;顶部为一半圆加一半椭圆构成的封闭曲线,其长轴为90.0m,短轴为70.0m;整个结构高度为41.0m。整个结构是由三角形网格构成的单层网壳体系,其中构成网格的大部分杆件采用矩形空心焊接钢管,在顶端一圈,为了加强整个结构的环箍作用,采用了矩形截面的实心杆件;杆件长度在1.5~3.5m 之间,截面高度为180~500 mm不等,宽度为65~120 mm不等。其中,绝大部分杆件的截面外边尺寸为65mm×180mm。结构模型如图1所示。
作用在结构上的荷载有恒荷载D、活荷载L(0.5kN/m2,考虑了满布L1及前后左右不均匀分布L2、L3、L4、L5 共5 种情况)、风荷载(采用风洞试验数据,考虑了 W0、W45、…、W315共8个方向角)、温度荷载(升温40度、降温20度)、地震荷载(X、Y、Z三个方向);所有杆件均采用Q345材料;底部节点在竖向为固定约束,沿曲面切线和法线方向为弹性约束,弹性刚度分别为 1.0×107kN/m和 2.5×106kN/m。
在结构整体稳定性分析中考虑恒、活、风三种工况的标准组合。如果对所有组合皆进行非线性“荷载-位移”全过程跟踪分析,在时间和精力上是不现实的。因此,先对各种组合进行线性特征值屈曲分析,根据计算所得到的荷载因子及相应的屈曲模态,确定最不利荷载组合,然后对其进行详细、深入的“荷载-位移”全过程跟踪分析。
3 线性特征值屈曲分析
根据“恒+活”、“恒+活+风”两种情况,共有93个标准组合,对每个荷载组合皆进行线性特征值屈曲分析。每种组合作用下结构的前三阶屈曲荷载因子见表1。
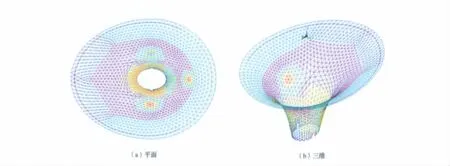
图1 第一号阳光谷结构模型图
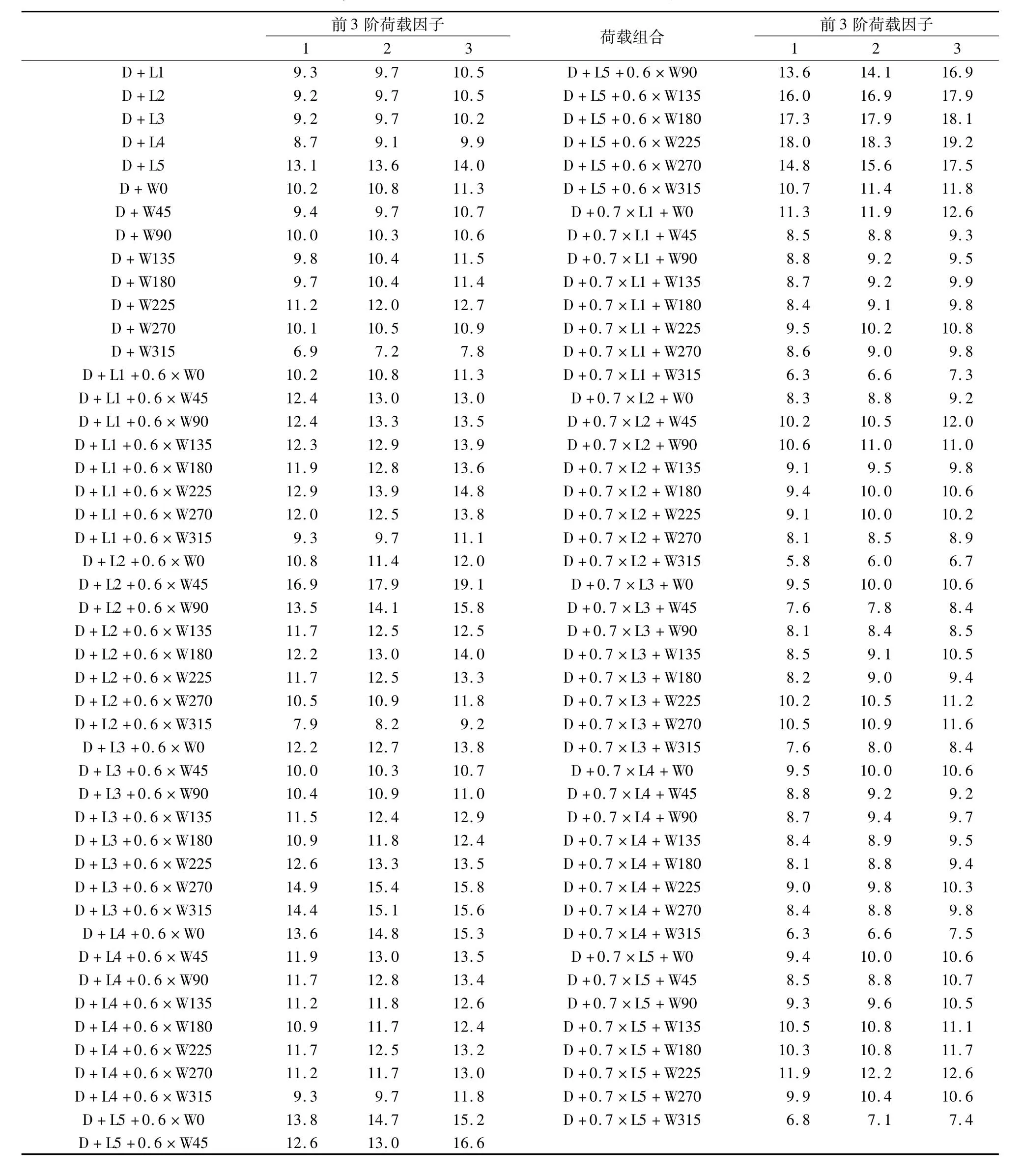
表1 各组合作用下的前3阶屈曲荷载因子
由表1可以看出,“D+0.7×L2+W315”组合作用下结构的第一阶屈曲荷载因子最小,为5.794。检查发现,每种组合作用下结构的前三阶屈曲模态均为整体屈曲。因此,“D+0.7×L2+W315”是结构整体稳定性分析中的最不利荷载组合,应作为后续非线性整体稳定分析的参考荷载。图2、图3分别给出了“D+L1”与“D+0.7×L2+W315”组合作用下结构的前三阶屈曲模态。
4 非线性整体稳定分析
4.1 几何非线性整体稳定分析
根据文献[3],对于网壳的稳定性可按考虑几何非线性的有限元分析方法进行计算,分析中可假定材料保持为线弹性。因此,在线性特征值屈曲分析的基础上,取“D+0.7×L2+W315”作为结构整体稳定分析的参考荷载,并假定材料为线弹性,利用“荷载-位移”跟踪技术对结构进行考虑几何非线性的稳定性分析。同时,利用“一致缺陷模态法”对结构进行考虑不同初始几何缺陷条件下的“荷载-位移”跟踪分析。初始几何缺陷的分布按照第一阶屈曲模态选用,最大缺陷值分别取10~270 mm不等,其中270 mm为结构悬挑长度的1/150。不同初始几何缺陷条件下结构的第一个临界荷载系数见表2,选取结构顶部短轴最外端484号节点作为考察对象,其“荷载-位移”曲线见图4。
由表2和图4可以看出,考虑几何非线性后,结构的稳定荷载因子为5.390 63,较线性特征值屈曲分析结果降低了6.96%;考虑1/150倍悬挑长度的最大初始几何缺陷以后,结构的稳定荷载因子为4.589 69,较线性特征值屈曲分析结果降低了20.8%。
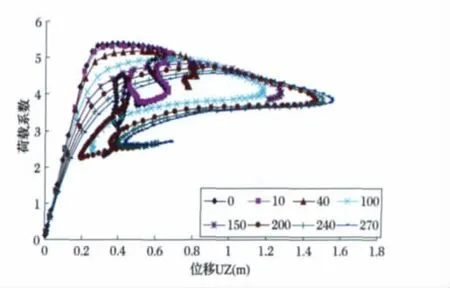
图4 不同缺陷条件下节点484的荷载-位移曲线
这说明几何非线性在结构整体稳定性分析过程中具有一定的影响,不可以忽视。根据文献[4],对规则的单层球壳、柱面网壳与双曲扁壳,稳定荷载系数取4.2。可以看到,考虑1/300倍结构跨度的初始几何缺陷后,仍可以满足此规定。
4.2 弹塑性整体稳定分析
在结构稳定性分析中,施加的最大荷载往往是使用荷载(组合)的几倍甚至十几倍,所以一部分构件可能会进入塑性。因此在“材料保持为线弹性”假定下得到的结果应用于实际工程时偏于非保守。所以,材料的弹塑性是结构稳定性分析中必须考虑的条件之一,而且文献[3]的条文说明中也鼓励进行考虑双重非线性的全过程分析。在实际应用中,假定钢材为双线性弹塑性模型。
仍然取“D+0.7×L2+W315”作为结构整体稳定分析的参考荷载,并考虑材料的弹塑性,仍采用上述分析方法,对结构进行弹塑性整体稳定分析。不同初始几何缺陷时结构的第一个临界荷载系数见表2,相应484号节点的“荷载-位移”曲线见图5。

图5 考虑弹塑性后节点484的荷载-位移曲线
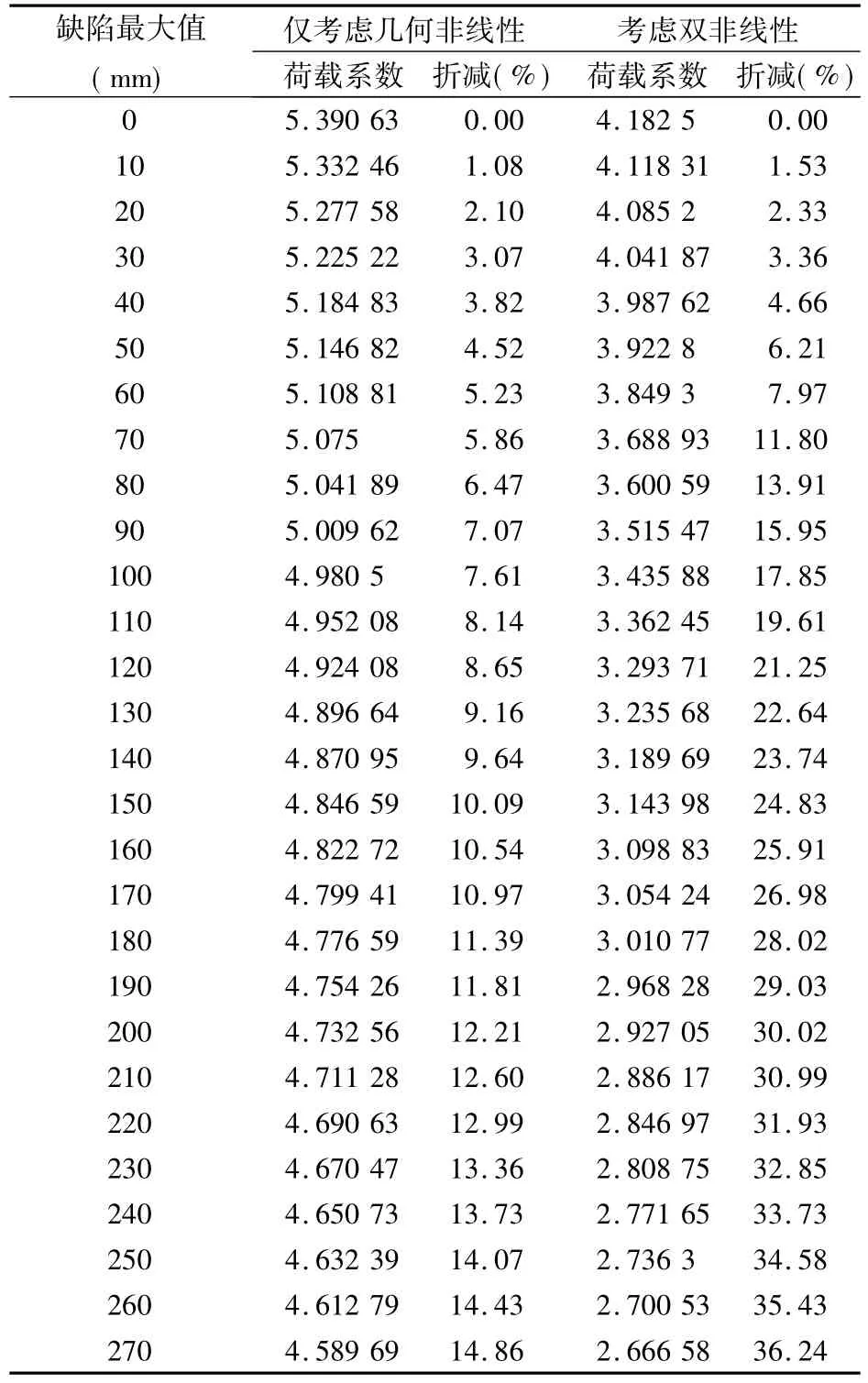
表2 不同初始几何缺陷时对应的荷载系数和折减率

图6 加载至第一个临界荷载时进入塑性的杆件
由表2可以看出,考虑钢材的塑性后,稳定荷载因子减小到4.182 5,较线性情况降低了27.8%,较仅考虑几何非线性情况减小了22.4%;而且随着缺陷值的增大,极限荷载因子也有所降低。这说明结构在达到第一个临界荷载之前,部分构件已经进入塑性工作状态。图6给出了加载至第一个临界荷载时进入塑性的杆件。可以看到,进入塑性的杆件处于悬挑根部,其中大多是竖向杆件,这些杆件具有较大的轴力。
由表2还可以看到,当最大初始几何缺陷值从0增加到60mm时,相应的极限荷载折减系数仅增加了8.0%,这说明当初始几何缺陷不是很大时,结构对缺陷并不敏感。但是当缺陷值达到结构最大悬挑长度的1/150时,相应的荷载因子可以折减到线性时的36.2%。根据现场实测数据,阳光谷钢结构节点的最大初始几何偏差为65mm。所以,可以认为实际结构的整体稳定荷载系数在3.6以上。根据文献[4],考虑材料弹塑性后,对规则的单层球壳、柱面网壳与双曲扁壳,稳定荷载系数取2.0。可以看到,考虑结构跨度1/300初始几何缺陷后,仍可以满足此规定。
5 结论
本文利用通用有限元软件ANSYS10.0对世博轴第一号阳光谷单层网壳结构进行了不同条件下的整体稳定性分析。计算结果表明,在弹性条件下,结构的极限稳定荷载因子可以达到4.58;考虑钢材的弹塑性后,在1/150悬挑长度的初始几何缺陷条件下仍可以达到2.6。此结构的失稳破坏后于强度破坏,极限稳定承载力满足设计要求。
虽然目前在结构稳定性分析方面有相关的规范作为基础,但是由于近几年来新型网壳的出现以及施工工艺等技术的提高,在实际工程的稳定性分析中还存在一些急需解决的问题。比如在最大初始几何缺陷选取时,针对球面网壳、柱面网壳及椭球面网壳等特定的结构形式文献[3]给出了1/300结构跨度的建议值,但是对于自由曲面等新型结构形式该如何选取还有待进一步深入研究。即使是针对球面网壳等常规形式,在现有施工技术条件下似乎也偏大,给实际工程的分析带来了一定的困难。
近几年网壳结构的发展又进入一个新的时期,出现了一些较为新颖的结构体系,特别是自由曲面结构的工程应用,似乎又代表一个新的潮流。对于这些新型网壳结构,其整体稳定性分析该如何进行,相应的参数该如何选取都是亟待解决的问题。
[1]尹德钰,刘善维,钱若军.网壳结构设计[M].北京:中国建筑工业出版社,1996.
[2]沈世钊,陈昕.网壳结构稳定性[M].北京:科学出版社,1999.
[3]网壳结构技术规程(JGJ 61-2003)[S].北京:中国建筑工业出版社,2003.
[4]赵基达,蓝天.《空间网格结构技术规程》的编制及其重点内容[J].建筑结构,2009,4.11-15.
The Research of Overall Stability Analysis of Sun Valley of Expo Axis
Cui Jiachun
(Tongji University,Shanghai200092,China;Shanghai Xian Dai Architectural Design(Group)Co.,Ltd.,Shanghai200041,China)
The project Expo Axis is a landmark building of Expo Shanghai 2010.Its roof system is composed of a cable-membrane structure and six free-form single-layer latticed shells named Sun Valley.Sun Valleys are different in shape and size and provide eighteen support points for cable-membrane structure.Because there is no clause used for free-form structure in current codes and specifications,it is difficult to carry on stability analysis for Sun Valleys.The Sun Valley NO.1 is studied for overall stability analysis in the paper.Ninety three load combinations are used in the process of buckling analysis,and D+0.7 × L2+W315 is selected as control load for nonlinear overall stability analysis.And then with different initial conditions considered the influence of geometric nonlinearity,plastic properties of material and initial geometric imperfection on overall stability of the structure are researched.The results show that the stability load factor of structure can meet the relevant specifications of China in every condition.Some members enter the plastic state when first critical load is reached,so the structure will enter strength failure before overall unstable failure happen.The outputs of the study will provide useful reference for design and analysis of other free-form projects.
Expo Axis;Sun Valley;Single-Layer Latticed Shell;Overall Stability;Initial Imperfection
TU311.2;TU393.3
A
1674-7461(2011)01-0073-06
崔家春(1982-),男,博士研究生,工程师。主要从事新型空间结构的设计与分析研究。E-mail:cuijiachun2000@yahoo.com.cn
