超深油气藏储层岩石孔隙度垂向变化研究

李武广，杨胜来，孙晓旭，隗雨薇

(1.中国石油大学，北京 102249;2.BECKBURY国际有限公司，辽宁 盘锦 124109)

超深油气藏储层岩石孔隙度垂向变化研究

李武广1，杨胜来1，孙晓旭1，隗雨薇2

(1.中国石油大学，北京 102249;2.BECKBURY国际有限公司，辽宁 盘锦 124109)

为了预测超深储层物性，采用超深储层孔隙度测井曲线数据，应用地质统计学，即实验变差函数来计算不同深度下孔隙度实验变差函数值，并拟合出孔隙度随油气藏埋藏深度连续变化关系表达式，总结了超深层油气藏储层岩石孔隙度随油藏埋藏深度或有效覆压的变化规律。同时，通过数学计算，对孔隙度进行处理和分析，建立了不同埋藏深度下超深层油气藏孔隙度随深度变化的宏观模型。该研究对深入了解超深层油气藏的产能及预测超深层油气藏的开发动态和采收率具有一定意义。

超深层油气藏;孔隙度;垂向变化;实验变差函数;地质统计学

引 言

随着常规油气藏勘探和开发程度的不断提高，超深层油气藏(行业标准SY/T6169－1995指深度超过4 000 m的油气藏)越来越受到各国重视，被视为油气资源接替的主要方向之一［1］。我国正在开发深度超过5 000 m的油藏，如塔里木盆地塔北隆起的东河塘油田(油藏最大埋深达6 130 m)，满加尔凹陷的哈得4油田，塔北地区的牙哈油田、桑塔木油田、羊塔克油田、塔河油田。在塔里木盆地还探明了深度超过5 000 m的气藏，其中羊塔克气田规模最大(气藏最大埋深达5 300 m)。国内外勘探开发的成功实例证明，超深层油气藏的开发具有可行性［2］。

超深层油气藏钻探成本高、风险大，其开发更面临新的技术挑战。因此需要大量、深入的超前性理论和技术研究。按照超深层深度4 000 m的定义看，现有油气藏深度的变化范围很大(国外已经发现最深的油气藏约9 000 m)。不同深度下油气藏的岩石物性差别及其随深度变化的规律是现场十分关心的问题［3］。若能建立某一地区岩石物性随深度分布的宏观模型，则可对不同深度的储层物性进行预测，对于指导探井设计具有重要意义。因此，对超深井的资料进行跟踪分析和研究，是一件既有科学价值又有实际意义的工作［4］。以塔里木盆地典型超深层油气藏地质特征为背景，深入研究超深层油气藏储层物性垂向变化规律，为超深层油气藏勘探开发提供技术支持［5］。

1 变差函数

变差函数是地质统计学中非常重要的一个基础工具，主要用来描述区域化变量的空间几何特性。研究区内的变差函数参数主要包括主方向(通常指连续性最好的方向)、次方向(与主方向垂直)及垂向上的变程值、块金值和基台值。为了能够精确地描述地质变量在空间的变化特征，根据变量在区域内的分布特点，设置相应的理论变差函数模型，然后再进行模拟计算［6］。

变差函数的定义:

式中:N(h)为相距为h的数据点对数目;γ*(h)为相距为h的变差函数值;Z(xk)为变量xk的期望值。

为了消除变差函数中的不稳定因素，得到任何一个方向、任何一步长所对应的变差函数值，就必须剔除进行实验变差函数计算时的特异值;针对不同的变量及其实验变差函数的特点，选取能反映区域化变量结构性特点的模型，调整模型参数的计算程序，以便于对变差函数进行最好的拟合。常用的变异函数模型有球状模型、指数模型、高斯模型和幂模型4种。本次模拟采用的是球状模型:

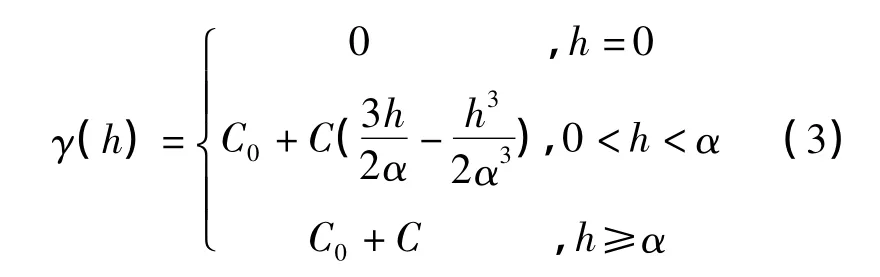
式中:γ(h)为拟合变差函数值;α为变程;C为拱高;C0为块金常数;C+C0为基台值。

变差函数的这些特征值反映了储层参数的空间变化特征，变程α的物理意义是指当距离超过某一范围后，变差函数值不再增大，而是稳定在一个极限值附近，这个范围就称为变程，这个极限值称为基台值(C+C0)。块金常数C0指原点处的变差函数值。变程α反映了区域变量的相关范围，当变差函数达到基台值时对应的α即为变量的变程。在变程范围内，区域化变量有空间相关性，α越小，反映区域化变量空间分布的相关性尺度越小，变化速度越快，随机性越强，相关性越弱;反之亦然。在变程范围外，区域化变量不存在空间相关性。变程α不仅能反映区域化变量的影响范围，还能直接反映储层参数沿某一个方向的变化速度的大小。

2 实例分析

应用变差函数理论，计算并分析塔里木油气藏的测井曲线数据(表1)。利用20个不同深度条件下的塔里木油气藏孔隙度数据，找出岩石孔隙度随埋藏深度的变化规律，建立相应的宏观计算模型。

表1 不同深度下的孔隙度

2.1 孔隙度实验变差函数的计算

选择变差函数计算的步长h为5 m，应用公式(2)，对实测孔隙度值进行实验变差函数的计算处理，可以得到在垂向上孔隙度随步长(深度)变化的连续函数值，即得到实验变差函数分布曲线(图1)。

图1 变差函数值分布曲线

2.2 孔隙度随深度曲线的拟合

选择有基台值的球状模型，利用计算得到的实验变差函数值，通过最小二乘法对其进行拟合。将式(3)分为3部分，其中当h=0时，比较简单;h＞α时拟合数据为常数，只要知道拟合数据的走势情况，也是比较简单的;0＜h＜α时，可以把式(3)看做1个含有2个参数的表达式，令b0=C0，b1=3C/2a，b2= －C/(2a3)，x1=h，x2=h3，y=γ(h)，这样式(3)的中间部分就变成了一个二元回归表达式:

由于x1、x2是已知的，对式(4)进行最小二乘计算，可以得到参数b0、b1和b2的数值，进而也就得到了变差函数的变程α、基台C0+C和块金值C0值。通过最小二乘拟合，得到拟合后的孔隙度随深度(步长为5 m)变化模型:

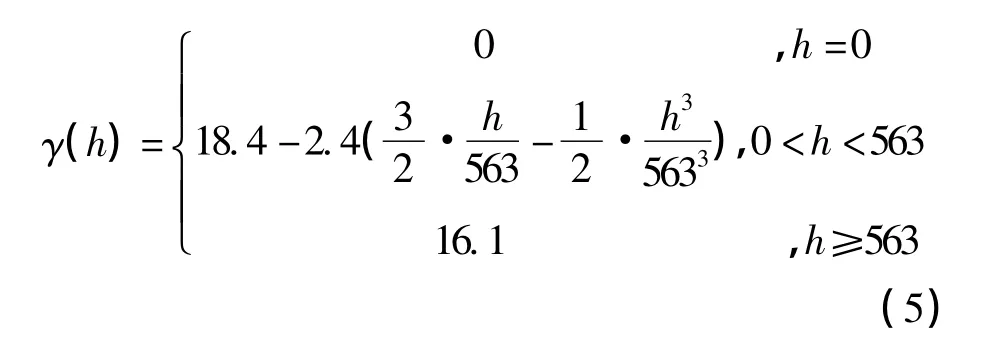
通过编写变差函数软件进行变差函数的计算和拟合，得到变差函数的变程、基台和块金值分别是563.1、18.44、16.1，代入步长 h就可以计算到任何一个步长所对应的的变差函数值(图2)［7］。

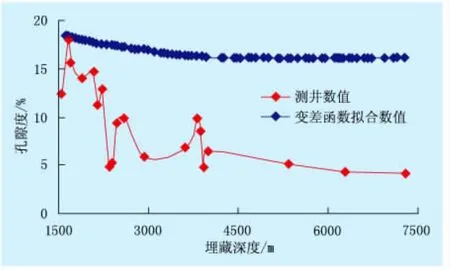
图2 实验变差函数拟合值分布曲线

2.3 超深储层物性垂向分布规律评价

通过计算分析可知(图3)，拟合后的模型是以5 m作为变差函数的步长，而且计算变差函数是以最小深度1 588 m为起点的，因此实际的孔隙度随埋藏深度的变程是4 373.8 m。由此可以得出，孔隙度随深度变化的范围是4 373.8 m。

图3 拟合前后孔隙度变化曲线

对于变差函数的表达式可以用一个指数函数来进行拟合，当储层埋深超过4 000 m后，孔隙度几乎不再随深度的变化而变化，趋于一定值。由于有效覆压与储层深度具有正相关性，进而说明了当有效覆压增加到一定值后，其对储层岩石的变形不再产生作用。在这一范围内，孔隙度可用下式表示:

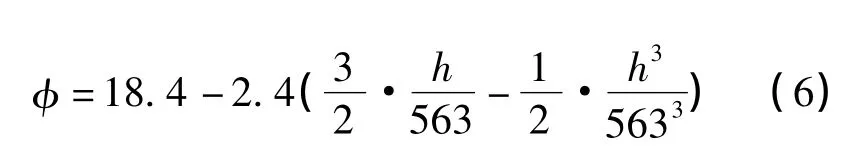
式(6)更好地体现了孔隙度的垂向变化规律。基台值表示当距离超过某一范围后，孔隙度不再增大，而是稳定在一个极限值16%，原点处的变差函数值，即块金值为18.4%，都说明了孔隙度随深度或者覆压的变化是非常合理的。在超深层油藏开发中，结合经济效益可以根据孔隙度变化范围打最优深度井，为现场钻井提供依据，从而更好地提高油气采收率［8－9］。

从图3还可以看出，变差函数计算的孔隙度与油藏埋深的关系曲线与测井数值相差不大，变差函数准确性高，其在超深层油藏中的应用成本低、简单、方便，应用前景较好。

3 结论

(1)随着深度的增加，储层岩石的孔隙度均呈下降趋势，这反映出压实作用使得储层岩石的孔隙度明显降低。

(2)有基台的球状模型合理地描述了油气藏孔隙度与埋藏深度在变程范围内的变化模型。

(3)通过变差函数理论研究储层物性垂向变化规律是一种新的理论方法，根据不同油田区块的孔隙度测井数据，可以建立适合不同油田区块的储层物性垂向变化规律宏观模型。该研究对深入了解超深层油气藏的产能及预测超深层油气藏的开发动态和采收率具有一定意义。

［1］高旺来.克拉2异常高压气藏开采压力变化对储层物性的影响［J］. 特种油气藏，2002，9(4):69－72.

［2］雷红光.上覆岩层压力下储层物性参数的整理方法［J］. 新疆石油地质，1995，16(2):78 －80.

［3］妥进才.深层油气研究现状及进展［J］.地球科学进展，2002，17(4):565－569.

［4］游俊.深部地层异常压力与异常孔隙度及油气藏的关系［J］.中国海上油气，1997，11(4):249－253.

［5］ Gandy，G R.Producing deep high pressure gas wells In The Anadarko Basin［C］.SPE7846，1979:1017 －1029.

［6］赵旭东.石油数学地质概论［M］.北京:石油工业出版社，1992:50－70.

［7］杨胜来，王小强，汪德刚，等.异常高压气藏岩石应力敏感性实验与模型研究［J］.天然气工业，2005，25(2):107－109.

［8］张之一.更新勘探观念开拓深层油气新领域［J］.石油与天然气地质，2005，26(2):193－196.

［9］石昕，戴金星，赵文智.深层油气藏勘探前景分析［J］.中国石油勘探，2006，19(1):1 －10.

Study on vertical porosity distribution in ultra－deep reservoirs

LI Wu－guang1，YANG Sheng－lai1，SUN Xiao－xu1，WEI Yu－wei2
(1．China University of Petroleum，Beijing102249，China;2．Beckbury International Co．，Ltd．，Panjin，Liaoning124109，China)

Ultra－deep reservoir quality is predicted by using porosity log and geostatistic method to calculate the experimental variation function of porosity at different depths，and by producing an expression of the variation of reservoir porosity with burial depth．The variation of ultra－deep reservoir porosity as a function of burial depth or effective overburden pressure has been generalized．Meanwhile，a mathematical model of porosity change with depth has been established．This study provides reference to understanding of ultra － deep reservoir deliverability and prediction of production performance and recovery factor．

ultra－deep reservoir;porosity;vertical distribution;experimental variation function;geostatistics

TE311

A

1006－6535(2011)05－0083－03

20101219;改回日期20110511

国家自然科学基金项目“超深层油气藏岩石物性垂向分布规律及渗流特征研究”(50874114)

李武广(1987－)，男，2007年毕业于东北石油大学电气信息工程专业，现为中国石油大学(北京)油气田开发工程专业在读博士研究生，主要从事油气田开发工作。

编辑 孟凡勤