考虑启动压力和二次梯度的压裂井稳态渗流模型
2011-01-03王永清章双龙杨玲智
张 强,王永清,章双龙,杨玲智,蒋 睿
(油气藏地质及开发工程国家重点实验室 西南石油大学,四川 成都 610500)
考虑启动压力和二次梯度的压裂井稳态渗流模型
张 强,王永清,章双龙,杨玲智,蒋 睿
(油气藏地质及开发工程国家重点实验室 西南石油大学,四川 成都 610500)
从质量守恒原理出发,推导了考虑启动压力梯度和二次压力梯度非线性单向渗流微分方程。并通过变量代换,将渗流方程线性化,获得单向稳定渗流模型的解析解。再利用保角变换将压裂井复杂的平面流动转化为简单的单向流动,最终获得考虑启动压力梯度和二次压力梯度的压裂井产量公式。通过对比分析可知:只考虑启动压力梯度或二次梯度项所得产能公式都是文中公式的特例;忽略二次梯度项将使计算所得产能偏低,忽略启动梯度项将使计算所得产能偏高,且误差随二次梯度项系数和启动压力梯度的增大而增大。
启动压力梯度;二次梯度;非线性渗流;压裂井;产能
引 言
近几年来,随着油气勘探开发的逐步深入,已经把勘探开发重点逐步转移到低渗透油气藏。一方面,理论研究、室内实验以及生产经验均表明低渗透储层中具有启动压力梯度,即只有生产压差大于某个数值,储层流体才会流动[1-2];另一方面,公式推导中曾经忽略的二次梯度作用带来的理论误差可达20% 以上[3-6]。针对该问题,本文从低速非达西渗流理论入手,同时考虑高阶梯度项,推导出了综合考虑2种因素的压裂井产能评价公式。通过比较分析可知,只考虑单一因素的产能公式是本文公式的特殊形式。
1 一维渗流模型的建立
假设条件:水平均质等厚条带状地层;地层一端有一直线供给边缘,另一端有一排液道,孔隙介质及渗透率均匀,各向同性;流体微可压缩且黏度是常数;忽略重力和毛管力。
低渗透油藏低速非达西渗流方程为:

式中:V为流体渗流速度,m/s;K为地层渗透率,10-3μm2;μ为原油黏度,mPa·s;p为地层压力,MPa;λ为启动压力梯度,MPa/m;x为距井底距离,m。
液体的状态方程为:

式中:ρ为液体密度,kg/m3;ρo为原始地层压力下液体密度,kg/m3;pi为原始地层压力,MPa;Cρ为液体等温压缩系数,MPa-1。
由质量守恒原理可得连续性方程为:

由▽算子的定义可得:

对液体状态方程先取对数再求导可得:

联立式(1)、(3)、(4)、(5)可得:

式(6)就是考虑二次梯度项和启动压力梯度的非线性渗流控制偏微分方程。
若对式(2)用麦克劳林级数展开并忽略所有高阶项,得:

二次梯度项出现的原因在于上述推导渗流控制微分方程的过程中没有对状态方程(2)做任何的简化处理。如果对状态方程用麦克劳林级数展开,用式(7)对渗流控制方程进行推导,导出的渗流控制方程不含二次压力梯度项。由于二次压力梯度项的存在,使得描述多孔介质、微可压缩液体流动的压力分布的微分方程呈现非线性特征。故常规线性渗流控制方程是非线性控制方程的近似与简化。

式中:q为井底产油量,m3/d;h为油层厚度,m;w为油层宽度,m;pe为油藏外边界压力,MPa;pw为生产井底的压力,MPa;L为油层长度,m;B为原油压缩系数。
当λ趋于零时,式(12)、(13)出现数学上求解%型的极限,应用洛必达法则可得到不考虑启动压力梯度的解式:

当Cρ趋于零时,式(12)出现数学上求解%型的极限,应用洛必达法则可得到不考虑二次压力梯度项的解式:
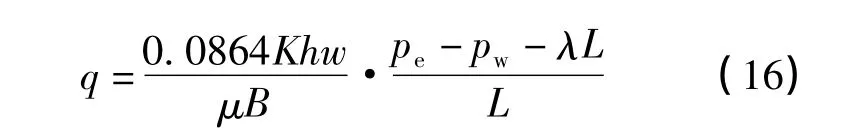
如果λ和Cρ同时趋于零,式(14)利用洛必达法则得到常规一维油藏产量公式:

2 压裂井渗流模型的建立
假设条件:均质等厚圆形油藏中心1口椭圆形裂缝井稳定生产;裂缝对称分布,无限导流,裂缝半长为Lf;产层全部打开,厚度为h;地层泄油半径为re,其压力为pe,井底压力为pw;地层均质且各向同性;压缩系数和黏度是常值;流体单相微可压缩;忽略重力和毛管力。
取保角变换为[9]:

式中:Lf为裂缝半长,m;Z、W为坐标平面。
变换后,图1(a)中的Z平面被映射为图1(b)中的W平面(W平面为宽度为π的带状地层)。

图1(a)中的裂缝AB经过保角变换映射成图1(b)中的A'B'。此时,Z平面内垂直裂缝井的复杂渗流问题就转变为W平面内简单的单向渗流问题。
可得相应的对应关系为:

式中:(X,Y)为Z平面的坐标,(U,V)为W平面的坐标。

3 产能误差分析
有关计算参数为:油藏有效厚度为20 m,渗透率为5 ×10-3μm2,供给半径为 1 000 m,裂缝半长为400 m,地层原油黏度为20 mPa·s,生产压差为10 MPa,原油压缩系数为 1.2。λ的值分别取0.001、0.050、0.100、0.500 MPa/m;Cρ的值分别取0.000 1、0.003 4、0.006 7、0.010 0 MPa-1。对应的误差如表1、2所示。其中误差的获得是以产量公式(25)为基准。由式(25)求得的产量为14.031 8 m3/d。
由表1、2可知,忽略二次梯度项将使计算所得产能偏低,忽略启动压力梯度项将使计算所得产能偏高,且误差随启动压力梯度和二次梯度项因子的增大而增大。

表1 二次压力梯度引起的误差

表2 启动压力梯度引起的误差
4 结论
(1)此次推导的单向流动压力分布公式(12)和产量公式(13)以及压裂井产量公式(22)综合考虑了启动压力梯度和二次梯度项的影响,贴近生产实际,应用范围更广泛。
(2)只考虑启动压力梯度或者只考虑二次梯度项的单向流动产量公式和压裂井产量公式分别是所推导公式(13)、(22)的特例。
(3)忽略二次梯度项将使计算所得产能偏低,而忽略启动梯度项将使计算所得产能偏高,且误差随启动压力梯度和二次梯度项因子的增大而增大。
[1]冯文光,等.单一介质、双重介质中非定常非达西低速渗流问题[J].石油勘探与开发,1985,11(1):56-62.
[2]贾振岐,等.低渗透油藏非线性渗流下的油井产能[J].大庆石油学院学报,2006,30(1):101-103.
[3]贾永禄,等.考虑二次梯度影响的渗流模型与试井样板曲线[J].西南石油大学学报,2007,29(5):69-71.
[4]聂仁仕,等.二次压力梯度非线性渗流理论与应用[J].大庆石油地质与开发,2010,29(5):96-103.
[5]同登科,郑利,王清河.考虑二次梯度影响的双重介质垂直裂缝井压力动态分析[J].力学季刊,2010,31(3):395-400.
[6]张伟东,杨铁军,蒋廷学,等.保角变换法用于计算压裂井产能[J].油气地质与采收率,2003,10(增刊):81-82.
Steady state flow model of fractured wells considering kickoff pressure gradient and secondary pressure gradient
ZHANG Qiang,WANG Yong - qing,ZHANG Shuang– long,YANG Ling– zhi,JIANG Rui
(State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu,Sichuan 610500,China)
Based on the principle of mass conservation,a differential equation for the nonlinear unidirectional flow considering the kickoff pressure gradient and secondary pressure gradient has been derived in the paper.An analytical solution was obtained for the unidirectional steady state flow model by linearizing the flow model through substituting the variants.The complicated plane flow of fractured wells was then converted to a simple unidirectional flow by conformal transformation,resulting in a production formula for fractured wells considering the kickoff pressure gradient and secondary pressure gradient.It can be learned by comparative study that the production formulas considering only the kickoff pressure gradient or secondary pressure gradient are special cases of the formula.Ignoring secondary pressure gradient will result in lower calculation values of production while ignoring kickoff pressure gradient will result in higher calculation values of production and the errors will increase with the increase of the secondary gradient coefficient and the kickoff pressure.
kickoff pressure gradient;secondary gradient;nonlinear flow;fractured well;productivity
TE312;TE348
A
1006-6535(2011)06-0089-03
20110323;改回日期20110802
国家科技重大专项“火山岩气藏完井优化与产能评价”(2008ZX05054)
张强(1985-),男,2009年毕业于大庆石油学院信息与计算科学专业,现为西南石油大学油气田开发专业在读硕士研究生,从事油气田开发方面的研究。
编辑 孟凡勤
