利用钻柱振动频谱判别钻柱复杂情况的方法
2011-01-03李春山王崇敬梁宏伟
李春山,王崇敬,陈 添,梁宏伟,孙 卫
(1.西北大学大陆动力学国家重点实验室,陕西 西安 710069;2.中国石油大学 石油工程学院,山东 青岛 266555;3.中国石油化工集团公司 西南石油局,四川绵阳 621000)
利用钻柱振动频谱判别钻柱复杂情况的方法
李春山1,2,王崇敬3,陈 添2,梁宏伟2,孙 卫1
(1.西北大学大陆动力学国家重点实验室,陕西 西安 710069;2.中国石油大学 石油工程学院,山东 青岛 266555;3.中国石油化工集团公司 西南石油局,四川绵阳 621000)
为实现钻井过程中井下钻柱运动状态以及井下复杂情况的实时监测,依据振动测试原理,结合实际钻井工况中钻柱振动特征,研制钻柱振动信号测量及处理系统。现场试验结果表明:钻柱出现黏卡、跳钻等现象后,利用快速傅里叶变换和小波变换处理方法可有效提取和识别钻柱在井下的振动特征;研制的钻柱振动采集系统可以应用于现场钻柱振动信号的采集、处理,其结果可以判断钻柱的井下工作状态。
钻柱振动;信号处理;井下状态;实时监测
钻进过程中钻柱所表现出的不同振动特性携带大量的井下信息[1]。通过钻进过程中钻柱振动信号的采集、处理和分析,判别井下钻柱运动状态以及井下复杂情况,是钻井工程中实时监测井下工况的一项重要技术。但如何有效提取钻柱振动信号并剔除干扰,且处理成可用于反映不同井下工况的可识别特征信号,是该项技术的关键。笔者通过钻柱振动信号测量和处理系统的研制及应用,研究钻柱振动信号的采集及处理方法,通过钻柱振动信号采集、处理及分析,判别井下钻柱工作状态。
1 钻柱振动信号的采集
钻柱在井内作为一根细长弹性杆件,有纵向振动、横向振动及扭转振动3种振动形式。振动分析的前提是要将振动以数字量或模拟量的形式采录下来。在数据分析中优先考虑的是数字量[2]。
1.1 振动物理量
在对振动进行测量时,能够直接测量的主要是运动量,即振动的位移、速度及加速度。从理论上讲,3个运动量之间存在明确的关系,可以任意选择测量的振动参量。但是,在实际测量中还需要考虑诸多客观因素,选取合理的测量参数。如振动位移是研究强度和变形的重要依据,加速度与作用力或载荷成正比关系,是研究动力强度和疲劳程度的基础,速度决定了噪声的高低,同时振动速度还与能量和功率有关,并决定了力的动量[3]。
经过理论与实践的分析,对于频率均低于400 Hz的钻柱纵振、横振和扭振来说,选用三维加速度传感器或速度传感器能够达到较好的分析效果。
1.2 钻柱振动信号的采集方式
考虑到可操作性和成本等因素,采用测振传感器进行地面测量的方法。在设计上充分考虑了低压、低功耗、抗噪声,防爆、防震、防水封装等安全因素。系统结构如图1所示。
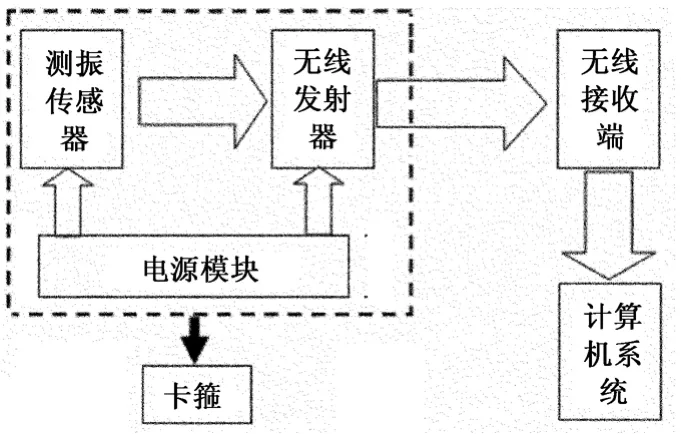
图1 钻柱振动采集系统设计结构示意图Fig.1 Sketch map of drill string vibration gathering system
前端数据采集部分主要由电源模块、测振模块和卡箍组成。由于振动信号的采集需要传感器进行长时间的工作,因此需要选择大容量电池对传感器进行供电,至少能保证持续供电超过7 d,采集部分的设备需要安装在钻柱上,对电池的体积也有所要求,理论上越小越好,且能方便更换并满足防水、防爆的需求。测振模块包括测振传感器和无线发射端等。由于前端振动传感器工作时要随着方钻杆同步转动,如果与后端数据处理计算机采用有线连接,则布线比较繁琐,并且远距离传输会引起较大的误差,给应用操作带来很多不便。因此,本设计采用了无线数据传输方式,使得布线工作大大简化,并可以达到实时监控的目的,有利于现场应用及设备的扩展应用。卡箍的作用是将整个前端的数据采集装置固定在钻柱上,确保安全、稳定地测量振动信号。
后端数据接收部分由无线接收端和计算机组成,它与前端数据采集部分之间采用无线通讯的方式进行点对点的传输。计算机将采集数据指令下达给无线接收端后,无线接收端向发射端发送指令,开始接收无线发射端数据。测振传感器测量的振动信号经A/D转换后传送到无线发射端,无线发射端将接收到的数据按照规定的协议进行打包,发送给无线接收端,最后传送到计算机进行处理分析。
考虑到加速度传感器比速度传感器轻,同时通过积分可实现加速度信号向速度和位移信号的转换,而速度传感器与位移传感器的信号经过微分求得加速度,其过程比较复杂,结果不可靠,因此常用加速度传感器作为测振传感器,测量加速度信号进行振动分析[4]。
2 钻柱振动信号分析方法与算法设计
在振动测试与分析的各种方法中,模态分析与参数识别技术是当前国内外发展迅速、应用最广泛的一种理论与试验相结合的方法。对振动系统动态特性的描述一般是在时间域、频率域和模态域内进行的[5]。近年来,随着分析技术的不断进步,逐渐开始进行时频分析,并将时域分析与频域分析相结合,目前主要采用小波变换分析技术。
2.1 时域分析方法及算法
振动信号的时域分析亦称为波形分析,主要是对时域信号的分析处理。常用概率和数理统计的处理方法有概率分布函数、概率密度函数、均方值、均值、方差和相关分析等。
如功率谱是用以表示振动信号在某频段的能量成分,振动信号在时间T内的平均功率可表示为

在算法设计上,功率谱密度函数一般是对相关函数进行傅里叶变换并求解[2]。
由于随机信号的每一个样本实现不可预知,所以须用所有样本功率密度的平均值来描述平稳的连续随机信号,因此功率谱函数反映在时域内随机信号自身与其他信号在不同时刻的内在联系,是钻柱振动时域分析的重要手段之一。
笔者采用的时域分析应用效果如图2所示。x代表纵向振动,y代表横向振动,z代表扭转振动。由图2可以看出:正常钻进时横向振动自相关性最好,即横向振动自身最有规律性;横向和扭转振动互相关性最好,说明钻柱的横向、扭转振动相互影响最大。

图2 XC26井正常钻进时钻柱振动数据相关性Fig.2 Data correlation of drill string vibration under normal drilling condition of well XC26
2.2 频域分析方法与算法
频域分析是建立在傅里叶变换基础上的时频变换,处理的结果是以频率为变量的谱函数。频域处理的主要方法是傅里叶变换,通过傅里叶变换结果的实、虚部,可转换成幅值谱和相位谱。随机振动信号的频域处理以功率谱密度函数为基本函数。通过其自功率谱和互功率谱可导出频响函数和相干函数。
钻柱振动的随机信号既包含周期振动又包含非周期振动(冲击振动),在时间域内很难分辨出振动特征,通过对钻柱振动信号的频谱分析可及时辨别钻头所钻遇地层的变化以及井下的工作状况。频谱反映振动信号在频率域随频率的分布特征,如幅值谱、相位谱、能量谱及功率谱等。钻柱振动信号的频谱分析以傅里叶变换为基础,目的是计算检测到的振动信号中各个频率成分及频率的分布范围,以及振动信号中各个频率成分的幅值,以获得显著频率成分和与之相对应的幅值(或能量)。
傅里叶变换是将采集到的时域数据转换成频域中的波谱,从而在频域中进行数据分析。对于钻柱振动信号,通过各个频段的谱分量分析可以得到振动信号的各个组成部分以及振动信号的来源和特征;通过频域的谱分析能够了解许多在时域里看不清楚的问题。岳喜枫等[6]在进行钻柱振动的检测与分析中,成功应用了傅里叶变换频谱图,对钻柱的振动信号进行了深入分析。近年来各种谱分析技术不断改进,傅里叶分析方法也得到了进一步的发展。
由于实际采集的振动信号以离散形式出现,傅里叶变换时需要N2次复数乘法和N(N-1)次复数加法,在N较大时计算量很大。为了减少运算次数,提高运算效率,在振动分析时采用的是基于时间的快速傅里叶变换算法(FFT)。所采用的蝶形算法[7]如图3 所示。

图3 蝶形算法示意图Fig.3 Sketch map of butterfly algorithm
2.3 小波变换分析与算法
钻柱在钻进过程中运行状态千变万化,经常发生不稳定振动或钻具故障,如钻头跳动、黏滑、钻柱偏转、钻头磨损和钻柱扭断等,都会导致动态信号的非平稳性的出现。同时,钻进过程中产生的振动信号伴随噪声信号。当钻柱出现故障时,其噪声品质也会发生改变。传统的时域分析和频域分析不能同时反映信号与时间和频率的关系,小波分析兼具时域和频域分析能力,且具有可变的时频分辨率,能较好地对非平稳信号进行分析。其基本原理是,通过小波变换将原始振动信号分解为不同的频率通道成分,并且对每一频率通道成分又按相位进行分解,频率越高,相位划分越细,反之越疏。为提高信号在低频段的精度,小波变换函数对低频段的小波分解系数进行了内插和抽样。因此,小波变换能有效地对整个频段进行分析,在机械振动分析中得到了大量应用[8]。
与快速傅里叶变换(FFT)类似,离散小波变换是一个快速线性运算,对于长度是2的幂次数据向量进行操作,将其变换为相同长度但意义不同的向量。
离散小波变换的优点是计算速度快,相对于连续小波变换,离散小波变换几乎可以瞬间完成,滤波频带在频率轴上也不会重迭,是真正的倍频程数据滤波。离散小波变换的缺点是数据由高到低每进行一次向量操作后可用数据减半,因此在某些应用场合,需要对变换后的数据通过内插和抽样进行恢复。
笔者采用一维Daubechies(db4)小波变换对XC26井正常钻进时采集到的钻柱振动信号进行分析,结果如图4所示。
由图4可见,小波变换分析方法对复杂工况下的钻柱振动信号分析有效。

图4 XC26井正常钻进时钻柱振动Fig.4 Drill string vibration of normal drilling in well XC26
3 现场试验结果分析
XC26井是四川盆地的一口直探井,设计完钻井深4.02 km,使用ZJ40D电动钻机进行钻井施工。试验井段采用的是塔式钻具组合:Φ215.9 mm钻头+回压阀+Φ177.8 mm无磁钻铤×1根+Φ177.8 mm钻铤×5根+震击器+Φ159 mm钻铤×9根+旁通阀+Φ127 mm加重钻杆×18根+Φ127 mm钻杆。试验井段的地层为三叠系须家河组。
该井钻至井深3.46651 km处钻柱出现黏卡,振动信号出现图5所示特征。
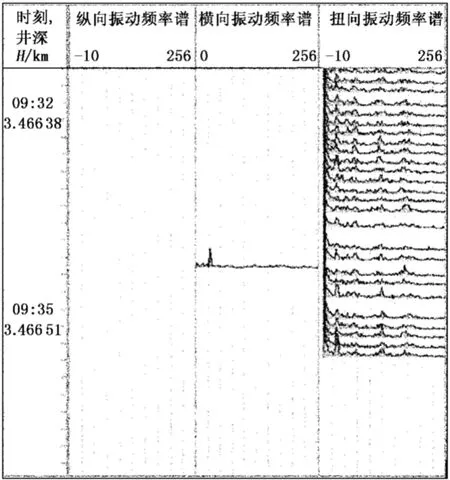
图5 钻柱黏卡时的三维加速度信号Fig.5 3-D acceleration signal while stuck pipe occurring
经频域分析后得到图6所示的分析图。钻柱轻微黏卡时,三维振动信号均有明显波动,其中扭转振动变化最剧烈。通过频谱分析后认为各向振动的频段分布变宽,幅值变大,且不同频段相差较大。此时,实际钻压波动为96~100 kN,转速波动为71~76 r/min,扭矩波动范围最大,为5.7~12.3 kN·m,判断为钻柱轻微黏卡。

图6 XC26井黏卡时钻柱三向频域分析谱与扭振分析图Fig.6 Analysis of three direction frequency spectrum and torsion vibration at differential sticking in well XC26
此外,该井钻至井深2.9372 km时,钻进过程频繁发生跳钻现象,岩屑掉块明显增多,钻柱振动信号出现如图7所示特征。
经时域分析发现,三向振动变化均较剧烈,其中纵向振动变化最剧烈,同时变化规律不明显,而横向加速度变化较均匀,个别点变化较大,扭向加速度变化分布相对较均匀。频域分析表明,除了低频部分很集中外,钻柱纵向、横向、扭向振动在50~250 Hz均有分布,说明在跳钻时钻柱振动信号频谱很丰富,但是同时也能看出,在跳钻时钻柱振动低频部分的振动幅值要比高频部分大得多(图8)。
通过对钻柱振动频谱的均值处理,在跳钻时钻柱纵向振动幅值最大为1~12 Hz,横向振动幅值最大为1~8 Hz,扭向振动幅值最大为1~14 Hz,即三向的振幅较大的部分都集中在低频段。这说明发生跳钻时,钻柱振动三向上的变化均较剧烈,其中纵向振动变化最剧烈,同时变化规律不明显,各向的频谱在低频、高频上均有分布,但低频部分的振动幅值明显高于高频部分。

图7 钻柱跳钻时的三维加速度信号Fig.7 3-D drill string acceleration signal while bit bouncing

图8 钻柱跳钻时的时域和频域分析Fig.8 Time domain and frequency spectrum analysis while bit bouncing
4 结论
(1)对钻柱振动频谱利用快速傅里叶变换和小波变换处理方法有效,可用于分析钻柱在井下的振动特征。
(2)研制的钻柱振动采集系统可以应用于现场钻柱振动信号的采集、处理,并通过钻柱振动信号处理结果可以判断钻柱的井下工作状态。
[1]王珍应,林建,施太和,等.钻柱振动特性分析与井底岩性识别方法初探[J].钻采工艺,2000,23(6):1-3.
WANG Zhen-ying,LlN Jian,SHI Tai-huo,et al.Analysis of vibration property for drilling string and discussion on recognition method of bottomhole lithology[J].Drilling & Production Technoldgy,2000,23(6):1-3.
[2]刘志国,陈实.钻柱振动信号的分析与应用[J].测控技术,2003,22(8):21-27.
LIU Zhi-guo,CHEN Shi.Analysis and application of drill string vibration signal[J].Measurement& Control Technology,2003,22(8):21-27.
[3]韩学岩,武庆河.钻具振动的三种基本形式[J].录井工程,2003,14(3):41-47.
HAN Xue-yan,WU Qing-he.Three types of drilling tools vibration[J].Mud Logging Engineering,2003,14(3):41-47.
[4]GABRIEL P G,JOAO Carlos Placido,CUNHA J C,et al.Drill string vibration:how to identify and suppress[R].IADC/SPE 39002,1997.
[5]孙月明.机械振动学:测试与分析[M].杭州:浙江大学出版社,1991:275.
[6]屈展,张绍槐.钻柱振动失稳突变模型的研究[J].石油大学学报:自然科学版,1994,18(1):35-38.
QU Zhan,ZHANG Shao-huai.Catastrophic model for vibration buckling of drilling string[J].Journal of the University of Petroleum,China(Edition of Natural Science),1994,18(1):35-38.
[7]刘清友,马德坤,钟青.钻柱扭转振动模型的建立及求解[J].石油学报,2000,21(2):78-82.
LIU Qing-you,MA De-kun,ZHONG Qing.A drilling string torsional vibration model and its solution[J].Acta Petrolei Sinica,2000,21(2):78-82.
[8]高岩,陈亚西,郭学增.钻柱振动信号采集系统及谱分析[J].录井工程,1998,9(3):44-51.
GAO Yan,CHEN Ya-xi,GUO Xue-zeng.The acquisition system for drill string vibration signals and the spectrum analysis[J].Mud Logging Engineering,1998,9(3):44-51.
Determining method for downhole drill string movement station by using drill string vibration frequency spectrum
LI Chun-shan1,2,WANG Chong-jing3,CHEN Tian2,LIANG Hong-wei2,SUN Wei2
(1.State Key Laboratory of Continental Dynamics of Northwest University,Xi'an 710069,China;2.School of Petroleum Engineering in China University of Petroleum,Qingdao 266555,China;3.Southwest Petroleum Bureau,SINOPEC,Mianyang 621000,China)
For real time monitoring of drill string movement during drilling and downhole problems,based on vibrating measurement mechanism and actual drill string vibration characteristics,a new system of measurement and process of drill string vibration signal was developed.The analysis results for field data show that when stuck pipe or bit bouncing occurs the vibration characteristics of drill string can be effectively extracted and identified by the methods of Fourier transform and wavelet transform.The system can be used to gather and process drill string vibration signals,and the result of signals process can help to determine downhole working condition of drill string.
drill string vibration;signal process;downhole condition;real time monitor
TE 258
A >
10.3969/j.issn.1673-5005.2011.05.010
1673-5005(2011)05-0056-05
2010-12-15
中国石油化工股份有限公司项目(JP10012)
李春山(1964-),男(汉族),四川德阳人,副教授,博士研究生,主要从事钻井、综合录井方面的技术研究和软件开发。
(编辑 李志芬)
