奥运会男子100 m跑成绩的灰色GM(1,1)模型预测
2011-01-02张正民
张正民
(西华师范大学 体育学院,四川 南充 637009)
奥运会男子100 m跑成绩的灰色GM(1,1)模型预测
张正民
(西华师范大学 体育学院,四川 南充 637009)
首先讨论了基于对数变换的GM(1,1)模型,并结合 C语言程序实现了该模型的程序化。然后以奥运会男子100 m跑为例,从专项训练学角度出发,结合自行编写的C语言程序进行数据处理、分析、验证,并预测了2012年第30届奥运会的男子100 m跑成绩在9.63~9.71 s。
科学计量学;竞赛成绩预测;灰色GM(1,1)模型;对数变换;奥运会男子100 m跑
体育成绩的预测是一个历久弥新的课题。随着体育以及其它相关领域如数学和计算机等学科的发展,准确迅速地预测体育成绩已成可能。预测未来奥运会成绩是当今各国体育工作者研究的热点之一,因为它关系到各国体育战略发展目标的建立与决策管理,是体育发展战略的基础和目标管理的依据,尤其是关系到一个国家或省市竞技主攻方向的选择、重点项目的布局与设置等。所以,对体育成绩的预测具有全局的、总体的和系统的战略意义。而灰色预测具有需要原始数据少、计算简单、预测精度高等特点,并且只需预测对象本身的单因素数据就可做出近期、中长期的预测[1]。由于田径成绩具有明显的灰色特征,又是奥运会的主要项目之一,因此,对其研究具有深远意义。
预测运动成绩与体育发展战略和训练决策密切相关,也是目标管理,制定具体训练方案的依据之一。预测和掌握未来世界运动水平的趋势,有利于我们在训练中统筹规划,控制训练过程,逐步逼近目标。因此,对运动成绩预测和研究是很有价值的工作。灰色预测GM(1,1)模型由于其具有需要原始数据少、计算简单、不需要预先知道原始的时间序列统计分布、预测精度高等特点而被广泛应用于体育成绩预测[2]。
体育成绩是时间轴上的数据序列,总体趋势呈现单调性(如本文中提到的男子100 m跑成绩总体呈单调递减趋势),由于成绩的影响因素复杂,因此成绩实际上是摆动的。以前大多采用传统的GM(1,1)模型或者改进的 GM(1,1)模型(如残差 GM(1,1)模型等)对其成绩进行预测[3-6]。而传统的GM(1,1)模型要求原始数据为光滑序列[7],原始数据越光滑,其预测模型越精确。但是原始数据是客观的,并不能像人们想象那样光滑,因此,预测模型的精确度受到了很大的影响,如何解决原始数据的不规则性,是首先要解决的实际问题。本研究在建模的同时结合C语言编程,对原始数据进行了对数变换[8](其它的变换方法有幂函数变换[9]、余切函数变换[10]等),提高了数据序列的光滑度,从而更适用于GM(1,1)模型,提高了预测精度。
1 研究方法
首先探讨了灰色预测 GM(1,1)模型及其检验方法。GM(1,1)模型的具体实施步骤包括:(1)对原始数据的处理,弱化随机性;(2)根据所选择白化微分方程,求解发展系数α和灰色作用量 u;(3)根据初始条件求累加生成序列,并还原求原始数据的模型序列。根据所描述的GM(1,1)模型,我们采用C语言自主完成了程序的编写,以方便今后的科研工作需要。该程序当前的功能和选择包括:①只需要输入原始数据序列。注意,原始数据序列的多寡会影响预测精度,这由用户自己选择决定和负责。②对原始数据的处理(即弱化随机性),提供了两个选择:直接累加和对数变换。其它的弱化随机性的方法也可根据需要实现;③打印输出中包括多种信息以方便随时分析使用,包括:原始数据的均值、方差和均方差,残差序列、相对误差,精度和滤波精度等等。
本研究选择二战后男子100 m跑最好成绩为原始样本。通过分析原始数据,并从专项训练学角度出发,结合数学函数的合理性,用C语言程序建模处理、分析数据,用基于对数变换的GM(1,1)模型对2012年奥运会男子100 m跑的成绩进行了研究和预测。
2 样本选取
选取1948年第14届奥运会到2008年第29届奥运会的历届男子100 m跑的第1名的比赛成绩和夺冠年份作为样本(见表 1)。全部数据来源于http://www.olympic.cn。这部分数据反映了第2次世界大战以后,奥运会100 m跑成绩的发展水平与趋势。

表1 1948~2008年奥运会男子100 m奥运会第1名成绩 s
3 灰色预测GM(1,1)建模及检验
3.1 灰色预测GM(1,1)模型[11]


3.2 灰色预测GM(1,1)模型的检验
灰色预测GM(1,1)模型的检验方法主要包括:(1)相对误差检验;(2)后验差检验;(3)关联度检验等[5]。
4 结果与分析
4.1 原始数据分析
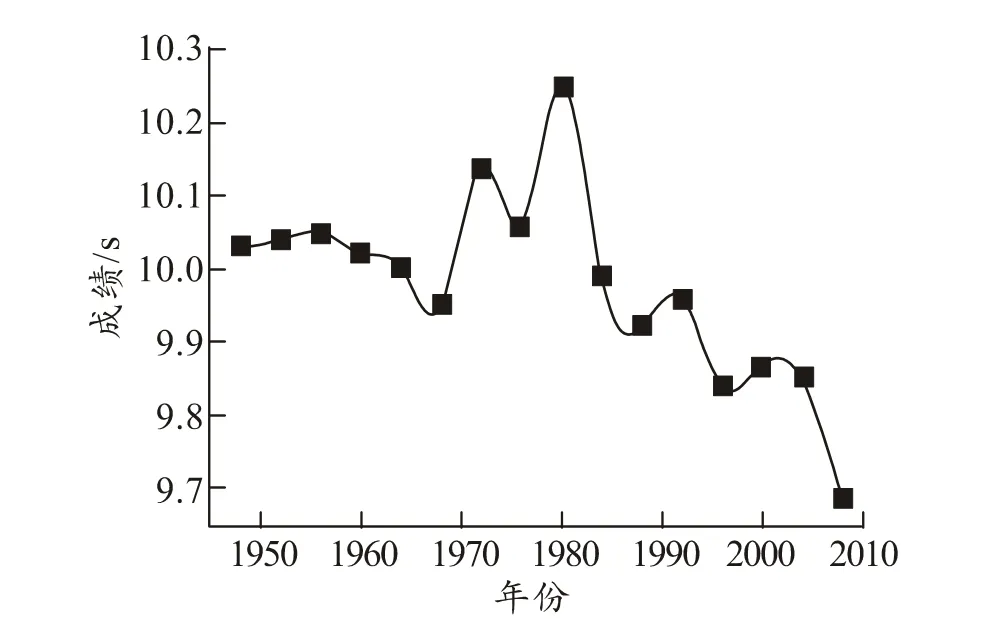
图1 二战后奥运会男子100 m跑第1名成绩变化
对1948~2008年奥运会男子100 m跑第1名成绩作图(见图 1)。由图1可知,1948~2008年间的成绩波动较大,很难用某个函数来拟合,即便是按照现代奥林匹克运动的发展阶段将其分成两个部分,即 1948~1976年,1980~2008年,波动性仍然较大,难以拟合预测。为了降低波动性,弱化随机性,对原始数据采用一次累加处理,将年代改为 1,2,3,…,16,如图 2。由图 2可知,累加生成序列可以由线性函数 Y=0.202 75+9.998 5X(X=1,2,3,…,16)拟合,相关系数R=0.999 9,因此在该线性函数下,原始数据序列中第n个成绩的模型值为yn=Yn-Yn-1=9.998 5,是定值,即线性处理后,预测值即为全部原始数据的平均值,所得到的成绩随时间不发生变化,显然是不合理的,这种预测没有任何意义;累加生成序列也可以由指数函数 Y=-3 707 691.839 34+3 707 692.042 78 eX/370833.34361(X=1,2,3,…,16)拟合,因此在该指数函数下,原始序列中第n(n=1,2,3,…,16)个成绩的模型值为:

此时其预测模型是有明确意义的,即预测值yn将会随着时间(这里为年代n)发生变化,这显然是合理的。

图2 累加生成序列
但是,通过函数拟合方法预测未来成绩时,所需样本数目一般都比较大,而且这种方法是完全建立在旧信息的基础之上的,即在旧信息足够的情况下,未来的信息是完全确定的,没有考虑到未来可能发生的变化,并且认为样本中所有数据对未来系统发展的贡献是完全一样的。显然在实际情况中,这是不合理的。比如,体育发展阶段的不同,各发展时期所表现出来的运动成绩的发展趋势不同,其对未来的贡献肯定也是不同的,一般来说越新的(时间上表现为越靠后)数据,对未来时间序列所起的贡献就越大。
4.2 灰色预测GM(1,1)模型预测的结果
文献[8]证明对数变换能够增加原始数据序列的光滑度,从而提高模型的预测精度。其它变换方法计算复杂,且对预测精度没有明显改善,因此不便应用。对数变换的GM(1,1)预测思想是:首先将原始数据采用自然对数变换后再用传统的GM(1,1)模型处理,最后还原即可。
1)第1部分(1948~1976年)建模分析。
通过反复建模分析,选择传统模型预测误差最小的6样本数(1952~1972年的成绩)作为预测1976年第21届奥运会男子100 m跑成绩的建模数据。然后采用基于对数变换的 GM(1,1)模型再进行建模分析(见表2)。从表 2看出,模型值与实际值非常接近。最大误差出现在1968年的墨西哥奥运会成绩(-9.95 s),由美国人詹姆斯·西恩斯创造。这是首次破10 s,且该纪录保持了15年之久。这种由天才运动员创造的记录属于偶然事件,所以会出现较大的误差。但是对于预测的1976年的100 m跑成绩,其误差仅为0.005 s,相对误差为0.05%,这是非常精确的。这说明了本研究选择的对数变换的GM(1,1)模型具有较高的预测精度。

表2 对数变换对1976年奥运会男子100 m跑成绩的预测
2)第2部分(1980~2008年)建模分析。
选择传统模型预测误差最小的 5样本数(1988~2004年的成绩)作为预测2008年第29届奥运会男子100 m跑成绩的建模数据。然后采用基于对数变换的GM(1,1)模型再进行建模分析(见图3)。

图3 1980~2008年实际值与模型预测值
从图3看出,模型预测值与实际值非常接近,1992年到2004年的100 m跑成绩误差为0.005~0.055 s。当然,2008年北京奥运会上,牙买加飞人乌赛恩.博尔特创造了新的世界记录 9.69 s。天才运动员的出现是不能包括在以往的信息中的,因此,产生了较大的误差。
以上两部分都是基于对原始数据对数变换的灰色GM(1,1)预测模型,容易看出,该方法简单实用,预测精度很高,适合于男子成绩100 m跑的预测。
3)对2012年奥运会男子100 m跑成绩的预测。
按照奥运田径运动发展阶段的划分,1980年以后的成绩反映了世界经济和科技高速发展的情况。因此,选择1980年以后的成绩,并结合对数变换预测了2012年奥运会男子100 m跑的最好成绩(见表3),同时考虑了不同样本数的预测情况。从平均相对误差来看,预测模型的精度是很高的。因此认为2012年奥运会男子100 m跑的最好成绩是9.63~9.71 s。

表3 不同样本数预测2012年奥运会成绩
4.3 灰色预测GM(1,1)模型预测的应用分析
体育成绩是时间轴上的数据序列,总体趋势呈现单调性,由于成绩的影响因素复杂,因此成绩实际上是摆动的。在一定程度上影响GM(1,1)模型预测准确度的因素是很多的,例如样本数、原始数据的平滑处理等都会影响模型预测精度。如果对原始数据进行对数变换、幂函数变换、余切函数变换等方法能增加数据序列的光滑度,从而更适用于GM(1,1)模型,在查阅参考文献,确认对数变换能够提高预测精度的情况下,采用基于对数变换的灰色预测GM(1,1)模型预测。由于同时考虑了不同样本数的预测情况,从平均相对误差来看,预测模型的精度是很高的。
对奥运会等大赛成绩的科学预测,是现代运动科学化训练的重要组成部分。我们以二战后奥运会男子100 m跑成绩为基础,以统计学和灰色理论为依据,结合计算机技术,运用编程方法,自行研发出一套应用系统;分析灰色预测GM(1,1)模型,自编程序实现了对成绩的GM(1,1)模型的预测。本研究所采用的基于对数变换的灰色预测GM(1,1)模型可以被用来进行成绩预测,且方法简单易行。本方法不仅在奥运会田径项目中适用,而且在其他项目中以及更重要的比赛中都有一定的适用性,诸如游泳、划船等测量类运动项目。该模型开拓性的预测方法,简便实用的操作过程,可为我们今后研究确定比赛成绩的预测工作提供参照模版,也可为其它竞技体育运动项目成绩的预测研究工作提供参考。任何预测都是建立在已有信息的基础上的,而未来不是过去的简单延续,因此,预测是有一定偏差的,但是该预测可以为目标管理决策部门或运动训练提供参考和依据。
[1]范振国. 运动训练控制领域中的灰色系统模型分析[J]. 体育学刊,2006,13(6):104-106.
[2]金川江,童丽平. 男子跳远全国纪录的等维灰数递补GM(1,1)模型及预测[J]. 体育学刊,2002,9(5):134-135.
[3]李毅青,邓宗琦. 1990,1994,1998,2002年亚运会部分项目成绩的预测[J]. 华中师范大学学报:自然科学版,1990,24(3):365-375.
[4]阎守扶,段赛勇. 对第26届奥运会田径成绩的灰色预测[J]. 中国体育科技,1996,32(5):60-62.
[5]张芝兰,徐明,刘艇. 对第27届奥运会游泳成绩的灰色预测[J]. 上海体育学院学报,1997,21(3):46-51.
[6]范文杰,周爱国,刘建敏. 对第28届奥运会田径运动成绩的灰色预测[J]. 北京体育大学学报,2002,25(6):847-849.
[7]邓聚龙. 灰色系统理论教程[M]. 武汉:华中理工大学出版社,1990.
[8]陈涛捷. 灰色预测模型的一种拓广[J]. 系统工程,1990,8(4):50.
[9]李群. 灰色预测模型的进一步拓广[J]. 系统工程理论与实践,1993,13(1):64.
[10]李翠凤,戴文战. 基于函数cotx变换的灰色建模方法[J]. 系统工程,2005,23(3):110-114.
[11]Chen Li-Hui. Using grey Markov forecasting model to examine the merger announcement affected the banks’stock values[J]. Journal of Grey System,2004,7:1.
Prediction of the result of men’s 100m run in the Olympic Games based on the grey GM(1, 1) model
ZHANG Zheng-min
(School of Physical Education,China West Normal University,Nanchong 637009,China)
Firstly, the author discussed the GM(1, 1) model based on logarithmic transformation, and realized the programming of this model by using C language. Then, by taking the men’s 100m run in the Olympic Games for example, from the perspective of the science of event specific training, the author carried out data processing,analysis and verification based on the program he compiled in C language, and predicted that the result of the men’s 100 m run in the 30thOlympic Games in 2012 would be somewhere between 9.63 s and 9.71 s.
scientific metrology;competition result prediction;grey GM(1,1)model;logarithmic transformation;Olympic Games;men’s 100 m run
G811.21
A
1006-7116(2011)04-0111-04
2010-10-24
张正民(1968-),男,副教授,硕士,硕士研究生导师,研究方向:体育教学与训练。
