无资料地区径流预报方法比较与改进

李红霞，张永强，敖天其，张新华

无资料地区径流预报方法比较与改进

李红霞1a，1b，张永强2，敖天其1b，张新华1b

（1.四川大学a.水利水电学院，b.水力学与山区河流开发保护重点实验室，成都 610065；2.CSIRO Land and Water，Canberra ACT Australia 2601）

利用新安江模型对无资料地区径流预报方法进行研究。以澳大利亚东南地区的210个流域为例，首先利用距离相近法、属性相似法和回归法进行预报，并对3种方法进行比较，结果表明，距离相近法精度最高，属性相似法次之，回归法效果较差。然后在距离相近法和属性相似法的基础上提出了综合相似法，使得模拟结果进一步提高。此方法可对中国无资料或者资料缺乏流域进行水文预报。

新安江模型；无资料地区；径流预报；区域化

无资料地区的径流预报具有重要的作用和意义［1，2］。目前对无资料地区径流预报常用的方法为区域化方法（regionalization）［3－8］，即通过某种途径，利用有资料流域的模型参数推求无资料流域的模型参数，从而对无资料流域进行预报。常用的区域化方法有空间相近法、属性相似法和回归法［6，7］。空间相近法是指找出与研究流域（无资料流域）距离上相近的一个（或者多个）流域（有资料流域），并把其参数作为研究流域的参数。其研究根据为同一区域的物理和气候属性相对一致，因此相邻流域的水文行为相似。属性相似法是指找出与研究流域属性（如土壤、地形和气候等）上相似的流域，并把其参数作为研究流域的参数。回归法是指根据有资料流域的模型参数和流域属性，建立二者之间的多元回归方程，从而利用无资料流域的流域属性推求其模型参数。

目前有不少研究对上述3种方法进行分析与比较。Young［3］利用6参数的PDM模型对英国260个流域进行研究，结果表明回归法优于距离相近法和属性相似法。Oudin［7］等利用GR4J和TOPMO模型对法国913个流域进行研究，结果表明距离相近法最优，属性相似法次之，回归法最差。Kay等［8］利用2个6参数的模型（PDM和TATE）对英国119个流域进行研究，结果发现对于PDM模型，属性相似法略优于回归法，而对于TATE模型，回归法表现最优。

以上研究结果不同原因在于，不同的研究采用不同的流域和数据；研究者对每种方法的使用也影响到结果的不同，如参考流域的个数，相似度的计算方法等；最后不同的研究采用不用的模型，也对结果有很大影响。同时，与率定结果相比，区域化预报的精度偏低，因此有必要进一步对区域化方法进行深入的研究和比较。本文以澳大利亚东南地区210个流域为例，对距离相近法、属性相似法和回归法3种方法在无资料地区径流预报的性能上进行研究和比较，并在此基础上提出了一种综合相似法。

1 新安江模型

新安江模型是赵人俊教授于1973年提出的降雨径流模型［9，10］，在湿润和半湿润地区得到广泛应用［11，12］。本文采用三水源模型，采用蓄满产流计算产流量；径流分为地面、地下和壤中流3种；采用三层蒸散发计算模型，3种水源均按线性水库计算河网总入流，河网汇流采用延迟滞时法。模型输入为降雨和潜在蒸散发，输出为径流，共包含14个参数：上层张力水容量UM，下层张力水容量LM，深层张力水容量DM，深层蒸散发系数C，张力水蓄水容量曲线方次B，不透水面积比例Im，表土自有水蓄水容量Sm，表土自由水蓄水容量曲线方次Ex，自有水蓄水水库对地下水的出流系数Kg，自由水蓄水水库对壤中流的出流系数Ki，壤中流消退系数Cg，地下水库消退系数Ci，河网蓄水量消退系数Cs和滞时L。

研究表明，当模型输入为降雨、蒸发时，模型能够优化的参数为5～8个［13］，简单的模型往往比复杂的模型能够取得更好的效果，为了减少需要优化的参数，本文将相对不敏感的参数C，Ex和Im固定，根据所研究的流域特性，分别设为0.15，1.2和 0。对于参数B，由于其大小与流域面积（A）相关，在本文中利用Log10（A）／10进行估算。这样本文中只有10个参数需要优化，参数的范围见表1。对于10参数模型和14参数模型的性能比较见图1，其中Kgi＝Kg＋Ki。

图1 10参数和14参数模型率定和区域化结果比较Fig.1 Calibrated and regionalized results of the 10-parameter model and the 14-parameter model

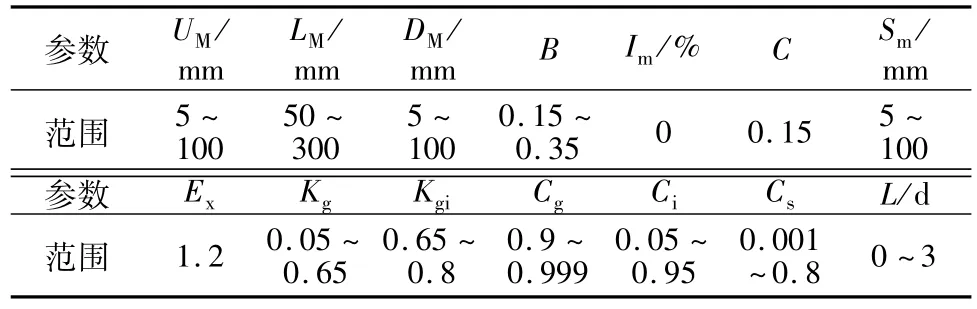
表1 新安江模型参数取值范围Table 1 Range of Xinanjiang model parameter values

2 研究区域和数据

本文以澳大利亚东南地区210个受人类活动影响较小的流域（流域面积为50～2000 km2）为例进行研究（图2）。表2给出了流域的水文气象特性，其中径流系数（多年平均径流与多年平均降水量的比值）为0.1～0.7，干旱指数（多年平均潜在蒸散发与多年平均降水量的比值）为1.1～3.6，可以看出大部分流域属于半湿润流域。模型输入采用2000- 2006年的日降水、日径流和日潜在蒸散发（由Priestley-Taylor公式估算），其中2000年数据用来预热模型。

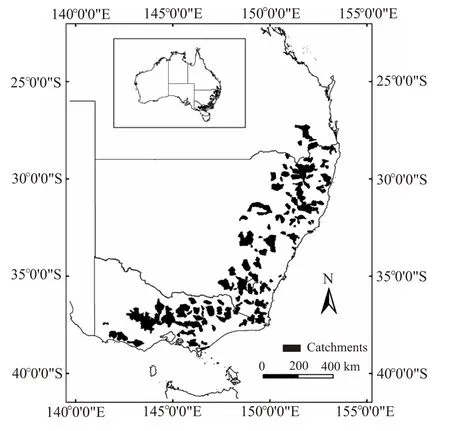
图2 研究流域的地理分布Fig.2 Locations of the catchments used in this study

对于距离相近法，2个流域间的距离利用流域质心间的经纬度进行计算。

对于属性相似法，本文采用如下4个属性（见表2）：

（1）干旱指数A（代表气候特征）；

（2）森林覆盖率W（代表植被特征）；

（3）流域坡度S（代表地形特征）；

（4）土壤持水能力P（代表土壤有效厚度）。

4个属性均采用多年平均值，并利用以下方程计算流域相似度

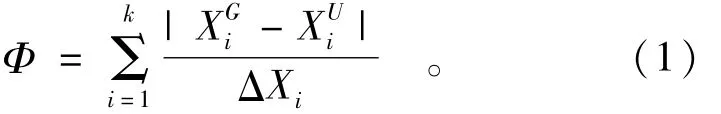
式中：XG和XU分别为有资料流域和无资料流域的k个属性；ΔX为属性最大值与最小值的差值；Φ的范围为0～1，Φ越小表示2个流域越相似。

对于回归法，仍然利用以上4个属性，分别建立每个参数与属性间的多元线性回归方程。

3 结果与讨论

3.1 模型率定与评价

本文以澳大利亚东南地区的210个流域为例进行研究，其中模型率定采用粒子群优化算法（ParticleSwamp Optimization PSO）［14］，目标函数采用 Nash－Sutcliffe有效性系数（NSE）（最大化）

表2 研究流域水文气象特性和属性特征Table 2 Summary of hydroclimatic characteristics and attributes of the catchments used in this study

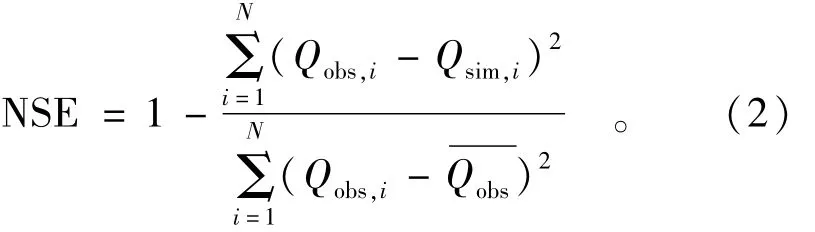
式中：Qsim和Qobs分别为模拟径流和实测的径流；Qobs为实测径流的算术平均值。NSE越大表明实测与模拟径流拟合越好，模拟精度越高。

对于模型区域化研究，首先我们采用粒子群算法优化得到每个流域的模型参数，然后将其中一个有资料流域人为假定成“无资料流域”（目标流域），然后利用其他209个有资料流域优化后的参数，采用区域化方法，获得“无资料流域”的参数并来驱动模型，即可得到无资料地区的模拟径流，最后将模拟径流与实测资料进行比较即可对模拟结果进行评价。同理，依次循环直到210个无资料流域都进行区域化。本文仍以Nash-Sutcliffe有效性系数对模拟结果进行评价。

图1为10参数模型和14参数模型的率定（a）和区域化（b）的NSE累积曲线（210个流域的NSE从大到小进行排序），其中区域化采用距离相近法。可见对于模型率定，10参数的结果与14参数无显著差别，对于无资料地区径流预报，10参数模型比14参数模型略优。图1说明了较少的参数由于减少了参数间的互相关性，提高了对无资料地区的预报。因此本文以下的研究均基于10参数新安江模型。

3.2 3种区域化方法的比较

对于距离相近法和属性相似法，可以采用一个或者多个参考流域。因此本文首先研究了参考流域个数对区域化结果的影响，当采用m个参考流域时，研究流域径流为利用m个参考流域的参数模拟径流的平均值，即第j天的径流为

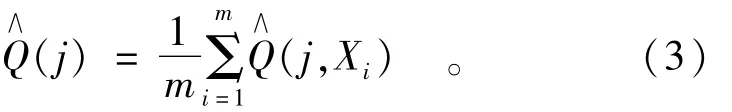
其中Xi为第i个参考流域的参数。

图3为选择1～100个流域作为参考流域时两种方法的模拟结果。可以看出，参考流域的个数对区域化结果有很大影响，选择多个参考流域模型的模拟精度明显高于仅选择1个参考流域的情况。但是随着参考流域个数的增加，模型精度不再增加，呈逐渐降低趋势。图3表明，对于本文研究，参考流域个数为2～5时模拟精度最高。

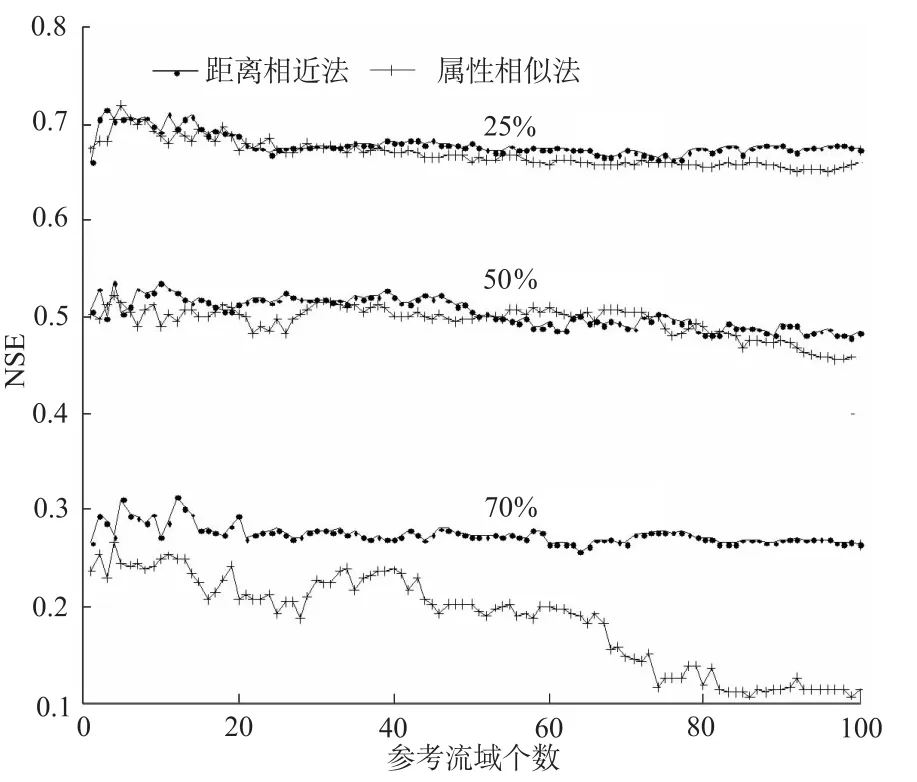
图3 参考流域个数对模型模拟精度的影响Fig.3 Impact of the number of reference catchments on simulation precision

表3 模型参数与流域属性间的相关关系及多元线性回归方程Table 3 Correlations between optimized model parameter values and catchment attributes and linear multiple regression equation

表3为模型参数与4种属性的相关系数以及参数与属性间的多元线性回归方程，回归方程中采用的流域属性利用显著性水平确定。表中第2～5列分别为参数与4个属性间的相关系数，第7列为方程的复相关系数。可以看出，模型参数与流域属性间相关关系不是很强，其中参数与单个属性的相关系数最大为0.32，方程的复相关系数最大为0.33，这与Oudin等［7］的研究结果相似。从表3还可以看出，在模型的10个参数中，表土自由水蓄水容量Sm与4个属性的相关关系最好，相关系数均为0.2以上，而在4个属性中，干旱指数（A）和森林覆盖率（W）与参数的相关性最好，所建立的10个方程中分别有6个和7个方程用到这2个属性。

图4为3种方法对无资料地区的径流模拟精度，其中距离相近法和属性相似法选择的参考流域个数为4。为了比较，图4同时给出了平均法的模拟结果，平均法即模型的每个参数均取所有流域对应模型参数的平均值。可以看出3种方法均好于平均法，其中距离相近法和属性相似法精度最高，回归法较差，仅比平均法略好。

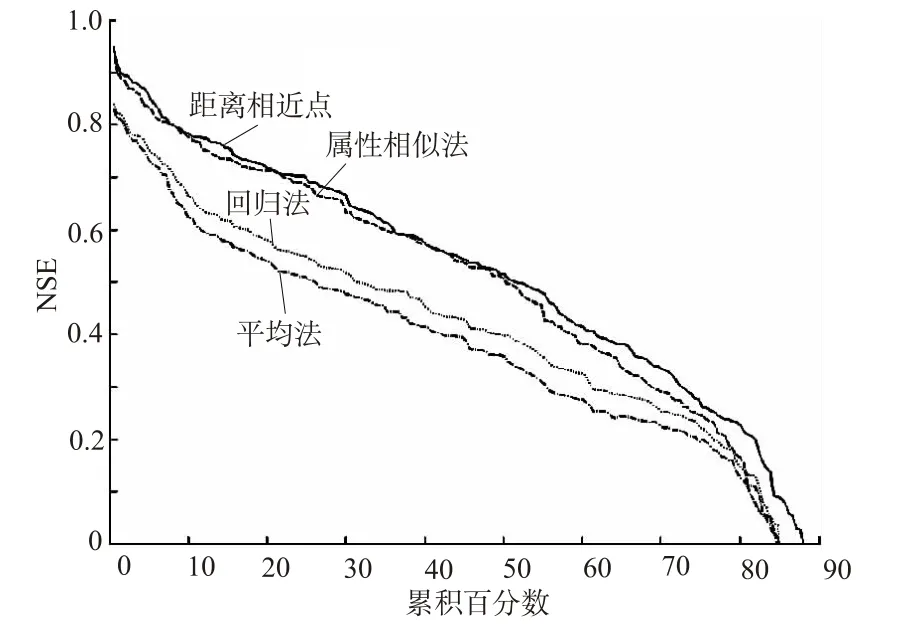
图4 不同方法对无资料地区的径流模拟结果比较Fig.4 Results of runoff prediction in ungauging catchments using different regionalization methods

平均法模拟精度最低，说明模型的参数具有一定的流域性，不同流域的参数不同。回归法模拟结果较差的原因可能为：①异参同效现象的存在，使得优化得到的模型参数具有很大的不确定性，因此很难建立参数与流域属性间的关系；②本文选择的流域属性不能很好地代表流域行为，模型参数与流域属性之间的相关性不强；③模型参数间存在一定的相关性。因此减少模型参数的不确定性或选择更有代表性的流域属性，可能会提高回归法的模拟精度。距离相近法与属性相似法结果接近，说明距离上相近的流域基本上具有相似的气候和物理属性。通过选择其他更有代表性的属性，有可能提高属性相似法对无资料流域径流预报的精度。

3.3 综合相似法

3种方法中，距离相近法和属性相似法原理相同，二者都是通过选取相似的流域，然后移用其参数到无资料流域。不同的是距离相近法选取距离上相近的流域，而属性相似法选取属性上相似的流域，因此将两种方法进行结合，有可能进一步提高无资料地区径流预报的精度。

在本文研究中，距离相近法略优于属性相似法，但是并非在所有流域中前者表现都好于后者（图5）。因此，本文在这两种方法的基础上提出一种综合相似法。在此方法中，距离（D）被作为一种属性，并与其他4种属性一起计算流域的相似度。我们采用如下方法进行属性之间的结合：由于单独利用距离已可以获得较好的结果，因此距离作为必选的一种属性，并分别与其他属性进行组合，产生了共15种组合，然后利用公式（1）计算流域的相似度，选择相似流域并进行径流预报。15种组合的预报结果见表3，在所有组合中，距离、干旱指数和森林覆盖率的组合效果最好，并且比距离相近法的NSE平均提高了约0.02（图6）。可见综合相似法一定程度上弥补了距离相似法和属性相似法的不足，使得径流预报的精度进一步提高。

图5 距离相近法和属性相似法的比较Fig.5 Comparison of spatial proximity and attributive similarity

图6 综合相似法与距离相近法比较Fig.6 Comparison of integrated similarity and spatial proximity

4 结 语

本文以澳大利亚东南区域210个流域为例，利用新安江模型对距离相近法、属性相似法和回归法进行研究和比较。结果表明，回归法由于模型的异参同效现象及参数与属性间的较弱的相关关系，模拟效果较差，在本文中仅比参数平均法精度略高。距离相近法和属性相似法模拟结果较好，其中前者略高于后者。此外，本文在距离相近法和属性相似法的基础上提出了综合相似法，使得预报精度进一步提高。

表4 不同属性组合结果比较（25%，50%，75%NSE）Table 4 Comparison of results with different attribute combination（25%，50%and 75%of NSE）

本文提出的方法也可以对中国存在的许多无资料或者资料缺乏的流域进行水文预报，从而增强对水资源的管理和利用。另外，如何在无资料地区径流预报中考虑模型参数的不确定性，将是下一步要进行的工作。

［1］ XU C Y.Estimation of parameters of a conceptual water balance model for ungauged catchments［J］.Water Resources Management，1999，13（5）：353－368.

［2］ YOUNG A R.Stream flow simulation within UK ungauged catchments using a daily rainfall-runoff model［J］.Journal of Hydrology，2006，320：155－172.

［3］ LI K Y，COE M T，RAMNKUTTY N，et al.Modeling the hydrological impact of land-use change in West Africa［J］.Journal of Hydrology，2007，337：258－268.

［4］ 王国庆.气候变化对黄河中游水文水资源影响的关键问题研究［D］.南京：河海大学，2006.（WANG G Q.Impact of climate change on hydrology and water resources in the middle reaches of the Yellow River basin［D］.Nanjing：Hohai University，2006.（in Chinese））

［5］ 张行南，井立阳，叶丽华，等.基于数字高程模型的水文模拟对比分析［J］.水利学报，2005，36（6）：759－763.（ZHANGX N，JINGL Y，YE L H，et al.Study of hydrological simulation on the basis of digital elevation model［J］.Journal of Hydraulic Engineering，2005，36（6）：759－763.（in Chinese））

［6］ MERZ R，BLOSCHL G.Regionalization of catchment model parameters［J］.Journal of Hydrology，2004，287：95－123.

［7］ OUDIN L，ANDRéASSIAN V C，PERRIN C，et al.Spatial proximity，physical similarity，regression and ungaged catchments：A comparison of regionalization approaches based on 913 French catchments［J］.Water Resources Research，2008，44：1－15.

［8］ KAY A L，JONESD A，CROOKSSM，et al.A comparison of three approaches to spatial generalization of rainfall-runoff models［J］，Hydrology Processes，2006，20：3953－3973.

［9］ ZHAO R J.The xinanjiang model applied in China［J］.Journal of Hydrology，1992，135：371－381.

［10］ 赵人俊.流域水文模拟－新安江模型与陕北模型［M］.北京：水利电力出版社，1984：106－109.（ZHAO R J.Hydrological modelling-Xinanjiang model and Shanbei model［M］.Beijing：China Water Power Press，1984：106－109.（in Chinese））

［11］ JAYAWARDENA A W，ZHOU M C.A modified spatial soil moisture storage capacity distribution curve for the Xinanjiang model［J］.Journal of Hydrology，2000，227：93－113.

［12］ 武新宇，程春田，赵鸣雁.基于并行遗传算法的新安江模型参数优化率定［J］.水利学报，2004，（11）：1－8.（WU X Y，CHENGCT，ZHAOM Y.Parameter calibration of Xinanjiang rainfall-runoff model by using parallel genetic algorithm［J］.Journal of Hydraulic Engineering，2004，（11）：1－8.（in Chinese））

［13］ SERBERT J.Multi-criteria calibration of a conceptual runoff model using a genetic algorithm［J］.Hydrology and Earth System，2000，4（2）：215－224.

Comparison of Regionalization Approaches for Runoff Prediction in Free of Observational Data Catchments

LI Hong-xia1a，1b，ZHANG Yong-qiang2，AO Tian-qi1b，ZHANG Xin-hua1b
（1a.College of Water Resource＆hydropower，Sichuan University，Chengdu 610065，China；1b.State Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu 610065，China；2.CSIRO Land and Water，Canberra ACT Australia，Canberra 2601，Australia）

This paper uses a conceptual rainfall-runoff model，the Xinanjiang model，to evaluate regionalization approaches using 210 catchments in south-east Australia as examples.Three regionalization approaches are compared：spatial proximity，physical similarity and regression.The results show that：spatial proximity provides the best regionalization solution；the physical similarity approach is intermediary；the regression approach is the least satisfactory.A new method，integrated similarity，is proposed by combining the spatial proximity and physical similarity.It turns out the integrated similarity further improves runoff prediction in free of observational data catchments.It is likely that taking into account the parameter uncertainty will improve the performance of predictions in free of observational data catchments.

Xinanjiang model；runoff prediction；free of observational data catchments；regionalization

P333

A

1001－5485（2010）02－0011－05

2009-01-14；

2009-06-03

国家自然科学基金项目（50979062）；国家科技重大水专项（008ZX07526－004－T007）

李红霞（1981-），女，山东烟台人，讲师，博士研究生，主要从事水文模拟及水文预报研究，（电话）15882160760（电子信箱）hx＿li406＠126.com。

（编辑：王 慰）