p-半线性映射的性质
2010-12-27王喜林刘丽红
王喜林,刘丽红,王 波
(吉林农业大学信息技术学院,吉林长春 130118)
p-半线性映射的性质
王喜林,刘丽红,王 波
(吉林农业大学信息技术学院,吉林长春 130118)
首次把p半线性映射引入到线性空间,并深入研究特征p域上的线性空间p半线性映射.给出了p半线性映射的一些基本性质,包含类似线性映射的一些性质和不同于线性映射的性质.
线性空间;p-半线性映射;完备域
现在对于特征零域上的线性空间和线性映射的研究非常成熟,应用也非常广泛,已经取得了相当系统的结果[1],于是我们开始考虑特征p域上的线性空间和p-半线性映射的情况.目前p-半线性映射在特征p域上的线性空间的应用,还处在前期的发展阶段,但是它在模李代数(即特征p域上的李代数)的分类起到非常重要的作用[2].本文把特征零域上的线性空间的线性映射的一些重要性质推广到特征p域上的线性空间,得到了p-半线性映射的一些重要性质.在此,如无另外说明,K均表示特征为p的域;V,W为K上的有限维线性空间.
定义1设K是任意一个给定的域,特征为p,其中p是一个素数.V,W是K上的线性空间.若有V到W的映射f满足

则称f是V到W的一个p-半线性映射.即f(β)可由f(α1),…,f(αn)线性表出.


推论1设f是V到W的p-半线性映射,则f把V中等价的向量组变成W中等价的向量组.
证明设{α1,…,αs}与{β1,…,βt}是V中等价的向量组,则αi可由{β1,…,βt}线性表出,βj也可由{α1,…,αs}线性表出,i=1,…,s;j=1,…,t.由命题1知f(αi)可由f(β1),…,f(βt)线性表出,f(βj)也可由f(α1),…,f(αs)线性表出,i=1,…,s;j=1,…,t.
故{f(α1),…,f(αs)}与{f(β1),…,f(βt)}等价,即f把V中等价的向量组变成W中等价的向量组.
命题2设K是特征为p的完备域,f是V到W的p-半线性映射,则以下结论等价:
(1)f把V中的某组线性无关向量变成W中的一组线性相关向量;
(2)f把V中某非零向量变成零向量.
证明(1)⇒(2).设{α1,…,αs}是V中的一组线性无关的向量且满足{f(α1),…,f(αs)}是W中的一组线性相关的向量,则存在不全为0的k1,…,ks∈K使

又K是特征为p的完备域,即K=Kp,故存在li∈K,i=1,…,s使得ki=lpi,i=1,…,s.则k1f(α1)+…+ks f(αs)=0,即lp1f(α1)+…+lps f(αs)=0,所以f(l1α1+…+lsαs)=0.又ki不全为0,故li不全为0.又α1,…,αs线性无关,故l1α1+…+lsαs≠0.则f把V中的非零向量l1α1+…+lsαs变成0.
(2)⇒(1).若有α∈V使f(α)=0,则f把V中的线性无关向量组{α}变为W中的线性相关向量组{0}.
定理1设U是V的子空间,f是U到W的p-半线性映射,则必存在V到W的p-半线性映射ɡ满足ɡ|U=f,称此ɡ为f的扩张.
证明设U′是U在V中的补子空间:

由分解唯一性知映射定义合理.则∀x=x1+x2,y=y1+y2∈V,k∈K.其中:x1,y1∈U;x2,y2∈U′.有

故ɡ是V到W的p-半线性映射,显然ɡ|U=f.
命题3设f1,…,fn是V到W的互不相同的p-半线性映射,则必存在α∈V,使f1(α),…,fn(α)两两不相同.
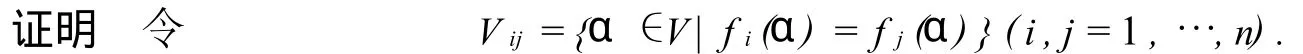
因fi(0)=fj(0)=0,故0∈V ij,又对每两个fi,fj,存在β,使fi(β)≠fj(β),故V ij是V的真子集.

kα∈V ij,则V ij是V的真子空间.
(ⅰ)若V ij都是V的非平凡子空间,则V中至少有一个向量不属于所有的V ij,设这个向量为α,则f1(α),…,fn(α)两两不同.
(ⅱ)若V ij中有V的平凡子空间V i0j0,则必有V i0j0=0,则∀α≠0有fi0(α)≠fj0(α),故可不考虑这样的V i0j0,其余的V ij便可归结为(ⅰ)的情形.
定义2设f是V到W的p-半线性映射,f的核定义为

命题4设f是V到W的p-半线性映射,则以下结论成立:
(1)f是单射⇔Kerf={0};
(2)f是满射⇔Cokerf={0}.
证明
(1)若f是单射,则只存在一个α∈V,使f(α)=0.但f(0)=0,故α=0,则Kerf={0}.
反之,设Kerf={0}.若有α,β∈V,使f(α)=f(β),则f(α-β)=f(α)-f(β)=0,故α-β∈Kerf={0},则α=β,f是单射.
(2)f是满射⇔Imf=W⇔W/Imf={0}⇔Cokerf={0}.
定理2设f是V到V的p-半线性映射,K是完备域(即K=Kp),则有
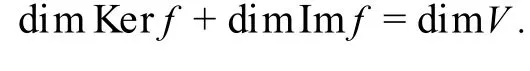

则f(es+1),…,f(en)是Imf的生成元,下面证明它们线性无关.
否则,若它们线性相关,则存在不全为0的ls+1,…,ln∈K满足

因K=Kp,故存在hs+1,…,hn∈K,满足hpi=li,i=s+1,…,n,则有f(hs+1es+1+…+hn en)=0,故
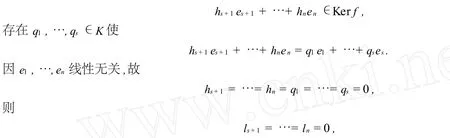
产生矛盾.故f(es+1),…,f(en)线性无关,并且是Imf的基,dim Imf=n-s=dimV-dim Kerf.
定理3设f是V到V的p-半线性映射,K是完备域(即K=Kp),则f是单射⇔f是满射.
由命题4和定理2知,f是单射⇔Kerf=0⇔dim Imf=dimV⇔Imf=V⇔f是满射.
定理4设f是V到V的p-半线性映射,K是完备域(即K=Kp),且dim Imf=r.则存在V到V的p-半线性映射f1,…,fr满足条件dim Imfi=1,i=1,…,r,且使得

证明不妨设dimV=n.因dim Imf=r,故dim Kerf=n-r.在Kerf中取基α1,…,αn-r,扩充为V的基α1,…,αn-r,β1,…,βr.由定理2的证明过程知f(β1),…,f(βr)是Imf的基.∀j∈{1,…,r}构造fj: V→V为
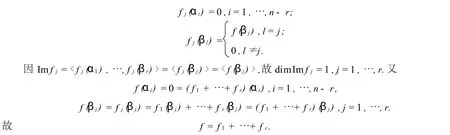
定义3设f是V到V的p-半线性映射,U是V的子空间.若对于任意的向量α∈U,都有f(α)∈U,就称U是p-半线性映射f的不变子空间,简称f-子空间.
例3f-子空间的和与交仍是f-子空间.
证明设V1,V2是V的f-子空间,下面证明V1+V2,V1∩V2是f-子空间.
易知V1+V2,V1∩V2是V的子空间.

故V1+V2是f-子空间.
∀v∈V1∩V2,则v∈V i,i=1,2.故f(v)∈V i,i=1,2,则f(v)∈V1∩V2,且V1∩V2是f-子空间.
命题5设f是V到V的p-半线性映射,U是V的子空间,e1,…,es是U的一组基,则
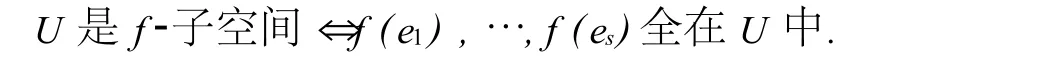
证明充分条件显然.下证必要条件.

[1] WERNER GREUB.Linear algebra[M].New York:Sp ringer,2009:1-185.
[2] STRADE H,FARNSTEINER R.Modular Lie algebras and their rep resentations[M].New Yo rk:Marcel Dekker Inc, 1988:300.
On the properties of p-sem ilinear mapping
WANG Xi-lin,L IU Li-hong,WANGBo
(College of Information and Technology,Jilin Agricultural University,Changchun 130118,China)
In this paper,the definition onp-semilinearmappings for linear spaces is first introduced and ap-semilinear mapping is investigated.Some elementary p ropertiesofp-semilinearmapings are given, w hich contain the same p roperties to linear mappings and the different p roperties from linear mappings.
linear spaces;p-semilinear mappings;perfect field
O 152.5
110·2125
A
1000-1832(2010)04-0021-05
2010-08-10
国家自然科学基金资助项目(10871057).
王喜林(1973—),男,硕士,讲师,主要从事代数研究;通讯作者:刘丽红(1975—),女,硕士,讲师,主要从事代数研究;王波(1973—),女,博士,副教授,主要从事线性代数和数量经济研究.
(责任编辑:陶 理)
