混源油定量判析方法研究新进展
2010-12-26陶国亮秦建中腾格尔张美珍付小东楼章华
陶国亮,秦建中,腾格尔,张美珍,付小东,楼章华
(1.浙江大学 地球科学系,杭州 310028;2.中国石油化工股份有限公司 石油勘探开发研究院 无锡石油地质研究所,江苏 无锡 214151)
全球范围内混源油气藏的普遍存在已成为共识,准确判断混源油气中各套烃源岩的贡献比例,确定主力烃源岩层,对于指导油气勘探具有重要意义[1-18]。从国内外已有文献来看,人工配比混源模拟实验(混源实验)是目前使用较多的判识混源油气烃源组成比例的方法。该方法是以代表不同烃源岩的油/气为端元,按一定比例进行人工混合,研究混合油/气的地球化学特征,分析地球化学指标随混合比例的变化规律,筛选出能够判断混合比例的指标,并用来定量识别混源油/气的烃源组成比例[1-10,19]。然而,尽管这一方法已得到广泛应用,但由于地质条件的复杂性,导致其在应用过程中仍存在待完善之处。笔者在总结前人研究成果的基础上,剖析了混源实验存在的待改进之处,并针对每一问题提出了相应对策;对比分析后认为,多元数理统计学方法可以在没有端元样品、不进行混源实验的情况下计算端元油数量、组成和混源比例,因而在计算混源油比例时具有特别优势,故对此方法进行了重点介绍。
1 传统混源实验法存在的问题
1.1 不同成熟度原油混源
如果某混源油存在2个油源,且这2个油源的油成熟度存在差异,那么它们的生物标志物浓度就会不同,按比例人工混合后,混合油的整体面貌往往受成熟度较低、浓度较高的原油控制。一般情况下,晚期生成的原油具有较高的成熟度,与早期生成的较低成熟度原油混合后,原油的整体面貌受控于早期原油,常规油气地球化学方法往往会错误判断混源比例。在实际地质条件下经常出现的一个情况是,具有较高成熟度的原油在运移过程中溶解混入了地层中的较低成熟度的有机质,即使溶解混入的量少,也会改变原油的整体面貌,影响油源对比的准确性。
在这种情况下,虽然生物标志物比值参数随混合比例递增或递减的趋势不变,但是其变化规律是非线性的,这就给建立混源油油源组成的定量判识模型带来难度。陈建平等[20]研究表明,在成熟度差异较大的情况下,二元混合时生物标志物比值参数与混合比例呈双曲线关系,三元混合时呈双曲面关系,四元及以上的多元混合时呈多维曲面关系,可见表达混源比例关系的方程式以及图版势必十分复杂。
1.2 高成熟或强降解原油混源
在中国南方海相碳酸盐岩油气藏中,烃源岩、原油、天然气往往都达到了高、过成熟演化阶段,常规生物标志物已经失效,突出表现为不同来源的原油和天然气往往具有相同的生物标志物特征,稳定碳同位素因为具有明显的热演化分馏作用,也难以进行精细的油源对比[21]。在原油遭受强烈降解后也会出现同样的情况。在这样的情况下,基于原油生物标志物和碳同位素的传统混源实验方法将无法起到有效的作用。
1.3 无法获得端元油/气
在一些复杂的盆地,油气混源情况十分普遍,导致无法直接获得准确的单源未混的端元油气样品,混源实验无法进行。
1.4 多源多期油气混源
目前除陈建平等[1-2]进行过三元混合模拟实验外,其他研究都是两元混合模拟实验,也就是说这些工作都是针对2期不同性质原油的混源进行的。而在实际地质条件下,多源多期成藏是常见现象,因此进行传统的两端元混源实验肯定是不够的,三元甚至更多元混源的情况都是常见的,实验和计算的复杂程度可想而知。
2 问题对策
特殊情况下的混源实验,虽然面临种种挑战,但是并非没有应对方法。笔者在总结前人研究成果的基础上,针对前文所述问题,总结了相应的对策和方法。
2.1 生物标志物定量
对于成熟度差异较大条件下的混源实验,虽然生物标志物比值参数变化规律复杂,但是混合油生物标志物的绝对含量是随着混合比例线性变化的。对特定生物标志物进行绝对定量分析,总结其随混合比例的变化规律,仍然可以通过线性方程定量判识混源比例。
2.2 特殊生物标志物筛选
对于高成熟或强降解条件下的混源实验,需通过充分的地球化学分析,筛选出生源意义明确、受成熟演化、运移和次生变化影响小的生物标志物,如三芳甾烷等[21]。针对这些生物标志进行混源实验,也同样可以定量判识混源比例。
2.3 多元数理统计学方法
对于无法获得端元样品情况下的混源油气判析,可以采用多元数理统计学方法。杜德文等[22]和Peters等[23]研究表明,可以在没有获得混合物端元组成、不进行混源模拟实验的情况下,通过多元数理统计学方法定量计算出混合物的端元数量、组成和比例。
杜德文等[22]研究了冲绳海槽沉积物物源组成的定量判识方法。通过数据成分化、初始端元成分求解、端元初始含量求解、调整初始端元获得最优端元与端元含量等4个步骤,成功完成了计算过程。并通过混源实验方法进行验证,表明多元数理统计学方法计算得到的端元成分与实际端元的相似系数接近“1”,端元组成比例与实际比例的误差仅为0.078,在可以接受的范围内。说明多元数理统计学方法成功计算出了沉积物的物源组成。
Peters等[23]研究了美国阿拉斯加州普拉德霍湾(Prudhoe Bay)74个石油样品。通过分析这些实际地质样品C19—C35之间的46个生物标志物浓度数据,利用一定的数理方法计算出该地区主要存在3套烃源岩,以及每个石油样品中这3套烃源岩的组成比例。并特别指出,通过该方法计算混源比例,可以不需要单源的端元油样品,也不要实验室人工配比模拟混源油样品。在计算中需要采用生物标志物浓度数据,而不是比值数据,因为比值数据随混合比例呈非线性变化[20,23]。
2.4 计算机协助处理数据
主要体现在以下2个方面:
一是处理多端元混源情况下复杂的数学计算。对于多元混源实验,理论上并没有任何问题,只是在定量计算的操作上存在难度,如果能借助计算机,通过特定软件来处理数据,那就会达到事半功倍的效果。
二是在多元数理统计分析过程中协助研究者完成复杂的数学推导演算。
3 定量计算混源比例的多元数理统计学新方法
通过前文对传统混源实验存在的问题及相应对策的分析可以发现,采用计算机协助、使用多元数理统计学方法计算混源比例,可以在未获得端元样品、不进行混源实验的条件下进行,这与传统方法截然不同。
3.1 数学原理
以两端元混合为例,设向量X,Y,Z分别代表端元油X、端元油Y和混源油Z的生物标志物浓度数据集:
X=(X1,X2,…,Xi);
Y=(Y1,Y2,…,Yi);
Z=(Z1,Z2,…,Zi)
又设f1,f2分别为混源油中端元油X,Y的比例,e=(e1,e2,…,ei)为不可测量的随机误差向量,
则有如下方程成立:
Z=f1X+f2Y+e
(1)
采用最小二乘算法对方程(1)进行拟合,使e2为最小,此时的f1和f2即为2个端元油的混合比例。
以两端元混源模型为基础,不难得到多端元混合模型,但是涉及的数学计算过程十分复杂,已超出本文讨论范围。
从两端元混源模型来看,实现该计算过程需要已知端元油和混源油的全部数据才能计算比例。然而在实际地质条件下,端元油很可能未知或不确定,该模型虽然原理正确,但是可操作性几乎为零。
本文采用的多元数理统计学方法的关键是基于已知混源油Z的组成,通过一定算法给方程(1)中的向量X和Y赋初始估计值,然后进行“交替最小二乘(Alternating Least Squares,ALS)”拟合,通过多元数理统计学算法不断改变端元赋值,进行迭代拟合,最终得到最佳的f1,f2和e的数值,同时也得到最佳的X,Y向量的值。不断赋值、拟合的计算过程相当复杂繁琐,因此可借助相关多元数理统计学计算机软件进行。
3.2 计算结果准确性验证
3.2.1 已知端元和比例情况
为了验证多元数理统计学方法计算混源比例的准确性,设计了如表1所示的端元样品、配比样品和比例的数据。其中smp1和smp11为端元样品,smp2~smp10是端元样品按比例配比组成的混源样品,var1~var7表示样品的组成参数,其数值均为定量数据。考虑到在测试实际样品时,实验误差无法避免,因此所设计的混源样品数据均不是绝对精确的、完全等于端元乘以比例的数值,而是在精确数据的基础上随机小幅波动。表1中同时给出了所有样品的人工配比比例。将表1中除比例之外的数据进行多元数理统计学计算。

表1 设定的端元样品和混源样品定量组成及混源比例
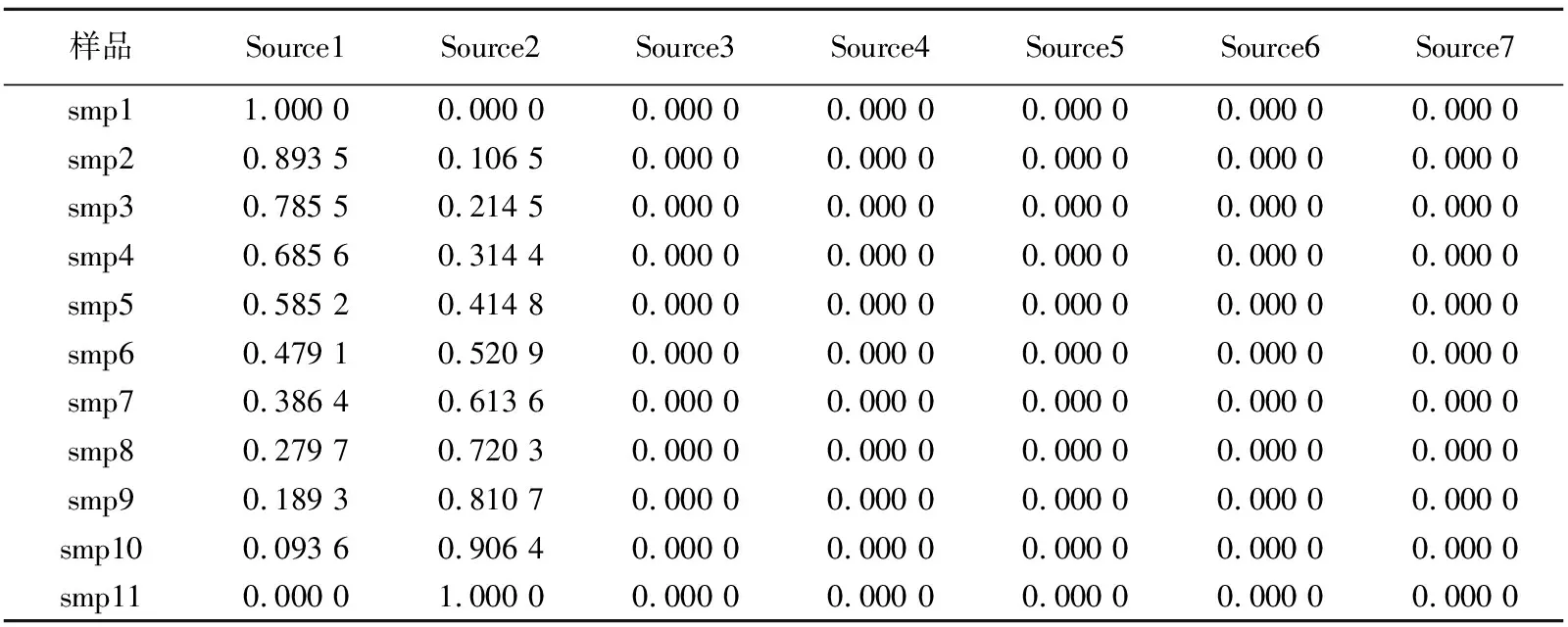
表2 多元数理统计学方法计算得到的混源比例
表2是交替最小二乘法计算结果,展示了计算得到的端元样品的数量和贡献比例。由表2可见,11个样品是由2个端元构成(Source3~Source7所占比例都是0),对比表1中的比例数据可以发现,Source1和Source2这2个端元的贡献比例计算值与实际值基本一致,所存在的微小差别是实验误差和数理统计学误差共同造成的,并不影响结果的准确性,可以忽略。
3.2.2 未知端元或比例情况
采集了某油田20个原油样品进行原油饱和烃萜烷类生物标志物(三环萜烷、四环萜烷和藿烷)定量分析,前人大量研究成果已经证实这些原油都是多套烃源岩、多期次混源形成的。采用多元数理统计学方法对20个原油的定量数据进行分析,结果表明其中存在4个端元,20个原油中4个端元的组成比例见表3。
为了验证计算结果的准确性,笔者根据每个样品的端元比例和端元组成,按公式(2)反推计算了每个样品的萜烷类生物标志物浓度:
Xc=X1f1+X2f2+X3f3+X4f4
(2)
式中:Xc代表某原油中生物标志物X的计算浓度;X1~X4代表端元油1~4中生物标志物X的浓度;f1~f4代表该原油中端元油1~4分别所占比例。
依次计算出全部萜烷类生物标志物浓度数据,得到20个原油的计算定量组成数据,将其与实际定量数据进行对比,可以判断出用多元数理统计学方法计算出的结果是否准确。
如图1所示,全部20个样品的计算生标浓度指纹与实际指纹非常一致,几乎重合,说明多元数理统计学方法计算结果正确。
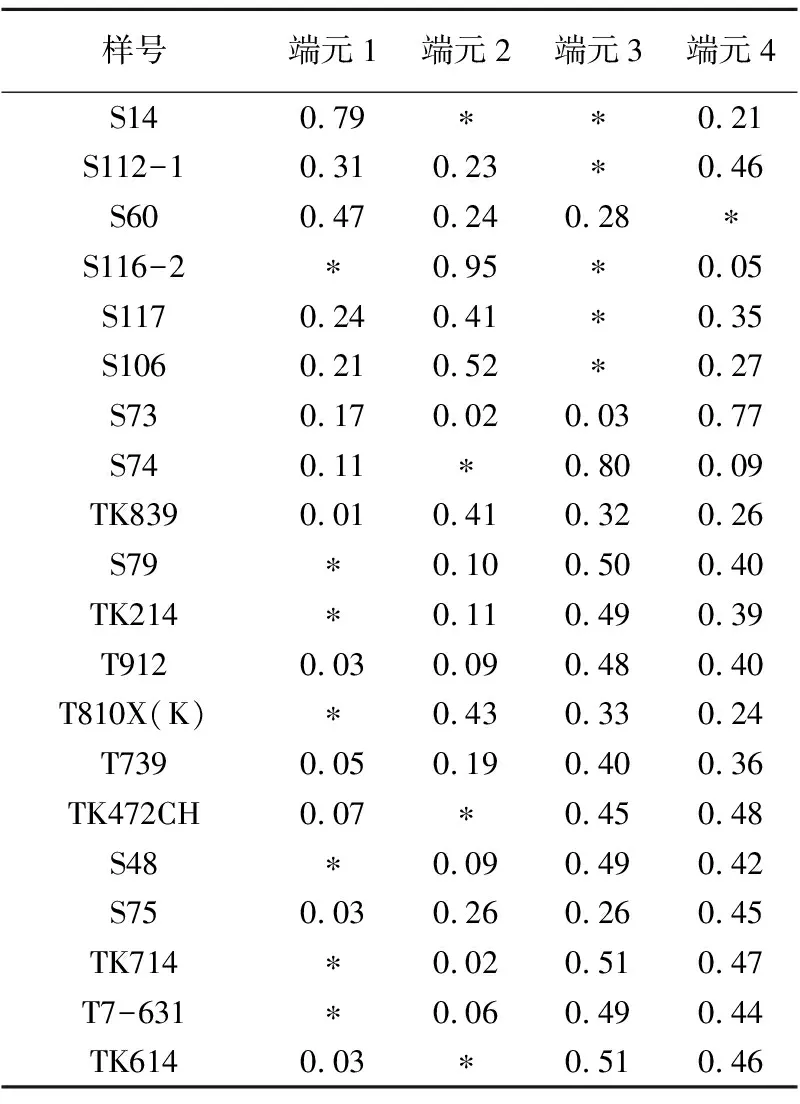
表3 20个原油中4个端元的混合比例
注: “*”表示充注比例很少。
4 结语
混源油人工配比模拟实验是常用的定量判析混源油气的方法。在成熟度差异较大、高成熟或强降解、无法获得端元样品和多端元混源的情况下,必须采用相应的应对策略:生物标志物定量、筛选特殊生物标志物、多元数理统计学方法和计算机协助处理数据,才能准确地完成定量判析。应用多元数理统计学方法,可以在未获得端元样品、不进行混源实验的情况下,采样“交替最小二乘”算法计算实际混源油的定量数据,得到端元的数量、组成和比例。复杂地质条件下,原油往往普遍混源,且单源未混的端元油样品一般无法得到,此时多元数理统计学方法就能够发挥巨大的作用。
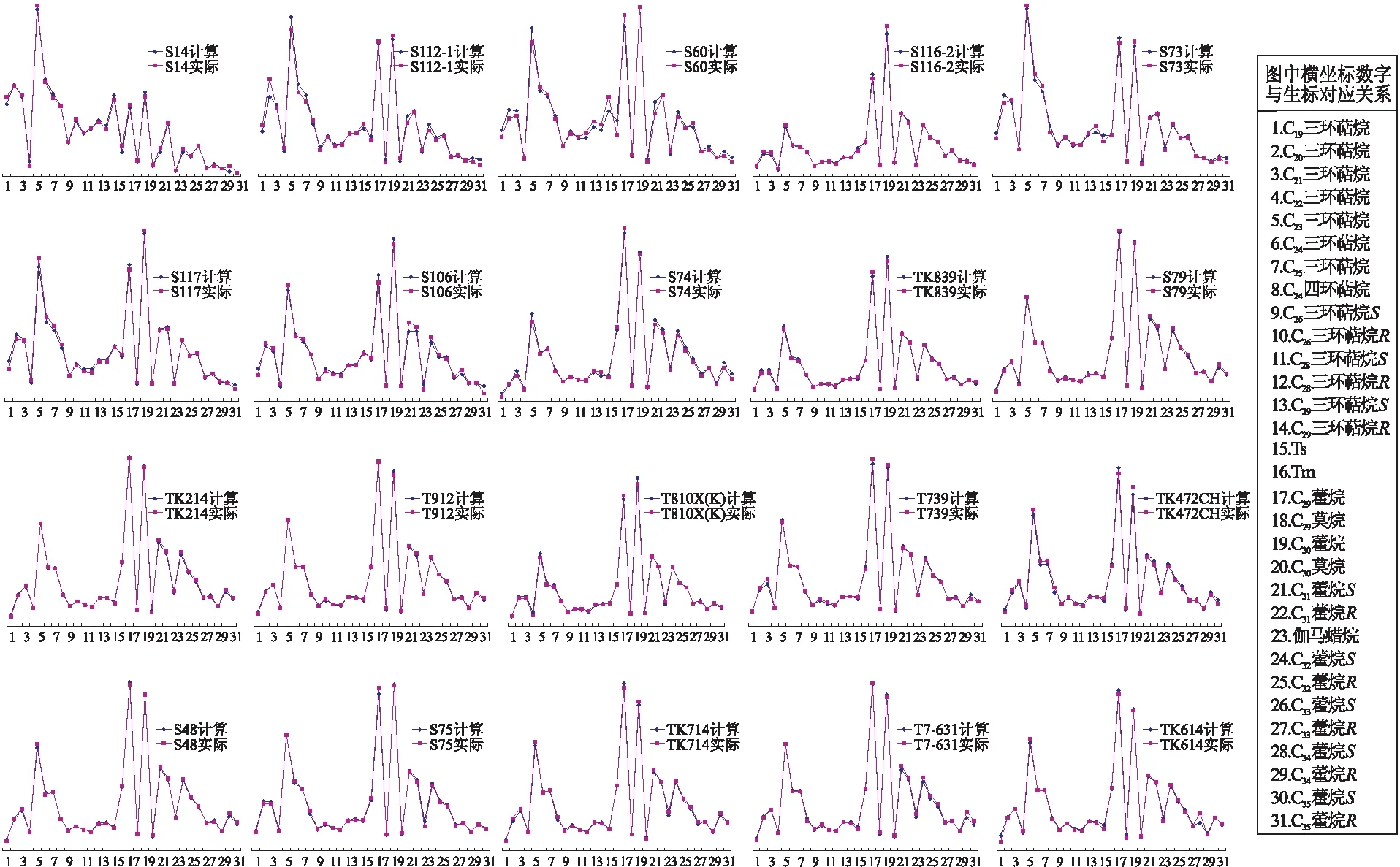
图1 多元数理统计学方法计算得到的生标指纹与实际指纹对比
参考文献:
[1] CHEN JIANPING, DENG CHUNPING, LIANG DIGANG, et al. Mixed oils derived from multiple source rocks in the Cainan oilfield, Junggar Basin, Northwest China, Part Ⅱ: artificial mixing experiments on typical crude oils and quantitative oil-source correlation[J]. Organic Geochemistry,2003,34(7):911-930.
[2] 陈建平,邓春萍,梁狄刚,等. 叠合盆地多烃源层混源油定量判析研究:以准噶尔盆地东部彩南油田为例[J]. 地质学报,2004,78(2): 279-288.
[3] 王铁冠,王春江,何发岐,等. 塔河油田奥陶系油藏两期成藏原油充注比率测算方法[J]. 石油实验地质,2004,26(1):74-79.
[4] 张振英,邵龙义,张世焕,等. 吐哈盆地台北凹陷西部弧形构造带混源原油特征[J]. 石油学报,2005,26(2):15-20.
[5] 程付启,金强,刘文汇,等. 鄂尔多斯盆地中部气田奥陶系风化壳混源气成藏分析[J]. 石油学报,2007,28(1):38-42.
[6] 郑亚斌,黄海平,周树青,等. 牛庄—八面河地区原油混源问题探讨及混合比计算[J]. 沉积学报,2007,25(5):795-799.
[7] 李水福,何生,张刚庆,等. 混源油研究综述[J]. 地质科技情报,2008,27(1):77-79.
[8] 李素梅,庞雄奇,杨海军. 混源油气定量研究思路与方法[J]. 地质科技情报,2009,28(1):75-81.
[9] 陶国亮,胡文瑄,曹剑,等. 准噶尔盆地腹部二叠系混源油油源组成与聚集特征研究[J]. 南京大学学报(自然科学版),2008,44(1): 42-49.
[10] 陶国亮, 胡文瑄, 曹剑, 等.准噶尔盆地腹部侏罗系原油勘探前景探讨[J]. 地质论评, 2008, 54(4): 477-484.
[11] 李素梅,庞雄奇,姜振学,等. 东营凹陷岩性油气藏混源相对贡献及石油地质意义[J]. 石油实验地,2009,31(3):262-269.
[12] ROONEY M A, VULETICH A K, GRIFFITH C E. Compound-specific isotope analysis as a tool for characterizing mixed oils: an example from the West of Shetlands area[J]. Organic Geochemistry,1998,29:241-254.
[13] 夏新宇,赵林,戴金星,等. 鄂尔多斯盆地中部气田奥陶系风化壳气藏天然气来源及混源比计算[J]. 沉积学报,1998,16(3):75-79.
[14] DZOU L I, HOLBA A G, RAMON J C, et al. Application of new diterpane biomarkers to source, biodegradation and mixing effects on Central Llanos Basin oils, Colombia[J]. Organic Geochemistry,1999,30:515-534.
[15] PETERS K E, CLUTSON M J, ROBERTSON G. Mixed marine and lacustrine input to an oil-cemented sandstone breccia from Brora, Scotland[J]. Organic Geochemistry,1999,30:237-248.
[16] ISAKSEN G H, PATIENCE R, VAN GRAAS G, et al. Hydrocarbon system analysis in a rift basin with mixed marine and nonmarine source rocks: the South Viking Graben, North Sea[J]. AAPG Bulletin,2002,86(4):557-591.
[17] JIANG CHUNQING, LI MAOWEN, OSADETZ K G, et al. Bakken/Madison petroleum systems in the Canadian Williston Basin, Part 3: geochemical evidence for significant
Bakken-derived oils in Madison Group reservoirs[J]. Organic Geochemistry,2002,33(7):761-787.
[18] ZHANG SHUICHANG, LIANG DIGANG, GONG ZAISHENG, et al. Geochemistry of petroleum systems in the eastern Pearl River Mouth Basin: evidence for mixed oils[J]. Organic Geochemistry,2003,34(7):971-991.
[19] 王文军,宋宁,姜乃煌,等. 未熟油与成熟油的混源实验、混源理论图版及其应用[J]. 石油勘探与开发,1999,26(4):34-37.
[20] 陈建平,邓春萍,宋孚庆,等. 用生物标志物定量计算混合原油油源的数学模型[J]. 地球化学,2007,36(2):205-214.
[21] 梁狄刚,陈建平. 中国南方高、过成熟区海相油源对比问题[J]. 石油勘探与开发,2005,32(2):8-14.
[22] 杜德文,孟宪伟,王永吉,等. 沉积物物源组成的定量判识方法及其在冲绳海槽的应用[J]. 海洋与湖沼,1999,30(5):532-539.
[23] PETERS K E, RAMOS L S, ZUMBERGE J E, et al. De-convoluting mixed crude oil in Prudhoe Bay Field, North Slope, Alaska[J]. Organic Geochemistry,2008,39(3):623-645.
