分数阶超混沌 Lü系统的吸引子讨论①
2010-12-26隋丽丽刘瑞芹
隋丽丽 刘瑞芹
(华北科技学院基础部,北京东燕郊 101601)
分数阶超混沌 Lü系统的吸引子讨论①
隋丽丽1②刘瑞芹2
(华北科技学院基础部,北京东燕郊 101601)
本文利用 Caputo意义下分数阶导数的概念,将整数阶 Lü系统拓展为四维分数阶的形式,通过分数阶导数的恒等形式,利用预估校正算法把分数阶系统进行了离散化,给出分数阶微分系统的近似数值解,从而刻画出其吸引子的状态。
分数阶导数;预估校正;吸引子
引言
混沌是非线性动力系统所特有的一种运动形式,它广泛的存在于自然界中,一般而言,混沌现象隶属于确定性系统而又难以预测(基于其动力学性态对于初始条件的高度敏感性),隐含于复杂系统但又不可分解 (具有稠密轨道的拓扑特性),已经呈现多种“混沌无序却又颇有规则”的图像 (如具有稠密的周期点)。如今,混沌的发现被认为是 20世纪最伟大的物理学三大成就之一。高维混沌系统的复杂性则可保证通信方面的安全,具有高维吸引子的混沌系统应用更为广泛,目前,它更是与许多的学科相互渗透,得到了广泛的应用。而分数阶高维混沌系统的研究是整数维的拓展,有更广阔的应用性,因此人们便对具有高维混沌吸引子的超混沌系统产生了浓厚兴趣,对其的关注和研究也越来越多,但目前对整数维超混沌系统的研究颇多,分数维超混沌系统的同步研究极其有限,而分数维超混沌系统研究更具现实意义。
本文是利用分数阶系统的预估校正算法把分数阶超混沌Lü系统离散化,给出分数阶微分系统的近似数值解,得到其逼近,并用 matlab进行数值模拟,描绘出该系统的超混沌吸引子及周期轨道。
1 Lü系统研究现状
吕金虎和陈关荣于 2002年通过混沌反控制得到如下的混沌 Lü系统[1],它的动力学
方程为:

其中x,y,z为实变量,且a,b和c是实参数,当参数取为a=36,b=3,18.0 基于Lü系统的超混沌系统同样具有研究的实际意义,超混沌 Lü系统是由陈爱寿等人于2006年提出的[5],其数学模型为 式中参数取为a1=36,b1=3,c1=20,在-1.03≤r1≤ -0.46,-0.46≤r1≤ -0.35,及-0.35≤r1≤1.3时,系统分别产生周期轨道、混沌吸引子以及超混沌吸引子的情况[6]。 目前还没发现对分数阶超混沌 Lü系统的研究,本文利用预估校正算子法研究分数阶超混沌 Lü系统的混沌及超混沌性态,说明分数阶超混沌 Lü系统存在超混沌阶数,利用数值模拟画出其吸引子图像,并求出其超混沌吸引子的指数谱及 Lyapunov维数,从而理论上验证了其超混沌性质。 首先考虑如下初值问题: 利用上述预估校正算法可得分数阶超混沌Lü系统离散化结果: 图 1 α=0.96时分数阶 Lü系统的超混沌吸引子Figure1 the attractor of fractional hyperchaosLüwhenα=0.96 图 2 α=0.99时分数阶 Lü系统的周期轨道Figure2 α=0.99 the periodic orbit of fractionalLüwhen 利用上述离散化方程,可以发现在分数阶Lü系统的确存在混沌和超混沌现象,利用数值模拟和 matlab可发现当参数a=36,b=3,c=12,r=-0.4,分数阶 Lü系统在 0.94≤α≤0.98时系统的吸引子是超混沌的,0.98≤α≤1时分数阶 Lü系统是周期的;其中α=1时的情况文献[6]已给出详细讨论。这就说明分数阶超混沌 Lü系统存在超混沌的阶数为 3.76~3.92。当上述参数不变,α=0.96时 Lyapunov指数谱为:λ1=0.0023,λ2=-0.202,λ3=0.0104,λ4=0.0115,有三个正的 Lyapunov指数,说明此时该系统的奇异吸引子是超混沌的,进一步计算出其 Lyapunov维数为 3.119。下图分别给出α=0.96,α=0.99时分数阶 Lü系统的超混沌吸引子与周期轨道。 本文利用预估校正算法对分数阶超混沌Lü系统进行分析,并用数值模拟刻画了该系统在参数在某一范围的混沌吸引子和周期轨道,从而为该系统混沌性质方面的应用提供了依据。 [1]LüJ.H.,Chen G.R.,Cheng S.Celikovsky,Bridge the gap be tween the Lorenz system and the Chen system[J].Bifurc.Chaos,2002,12(12):2917-2926 [2]Ju H.Park.Adaptive synchronization of hyperchaotic Chen system with uncertain parameters[J].Chaos Solitions Fract,2005(26):959-964 [3]Han X,Lu J A,Wu X.Adaptive feedback synchronization of Lüsystem[J].Chaos Solitions&Fractals.2004,22(1):221-227 [4]Wu Xiangjun.Chaos in the fractional order unified system and its synchronization[J].Chinese physics,2007,16(7):392-401 [5]Chen A M,LüJ A,J H,etc.Generating hyperchaotic Lüattractor via state feedback control[J].Physica A,2006(364):103-110 [6]M.T.Yassen.Synchronization hyperchaos of hyperchaotic systems [J].Chaos,Solitions&fractals,2008(37):456-475 [7]Diethelm,K.,Ford,N.J..Analysis of fractional differential equations[J].Mathematical Analysis and Applications,2002(265):229-248 Discussion on THE Attractor of Haperchaotic Lü SUI Lili,LIU Ruiqin (Noth China Institute of Science and Technotogy,YanjiaoBejing-East 101601) In thispaper,we give the integer-orderLüsystem an expansion for the four-d imension fractionalorder under the sense of Caputo fractional derivative concept for the first t ime.And also we give the approximate numerical solution of the differential system using predictor-corrector algorithm for the fractional-order system of the discretization,which depicts the attractor state. fractional derivative;predictor-corrector;attracor 019 A 1672-7169(2010)02-0084-05 2010-01-14基金项目:国家自然科学基金项目,项目批准号:60872062 隋丽丽 (1983-)女,硕士,华北科技学院基础部教师。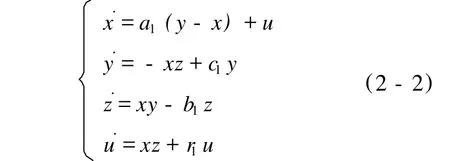
2 离散化过程



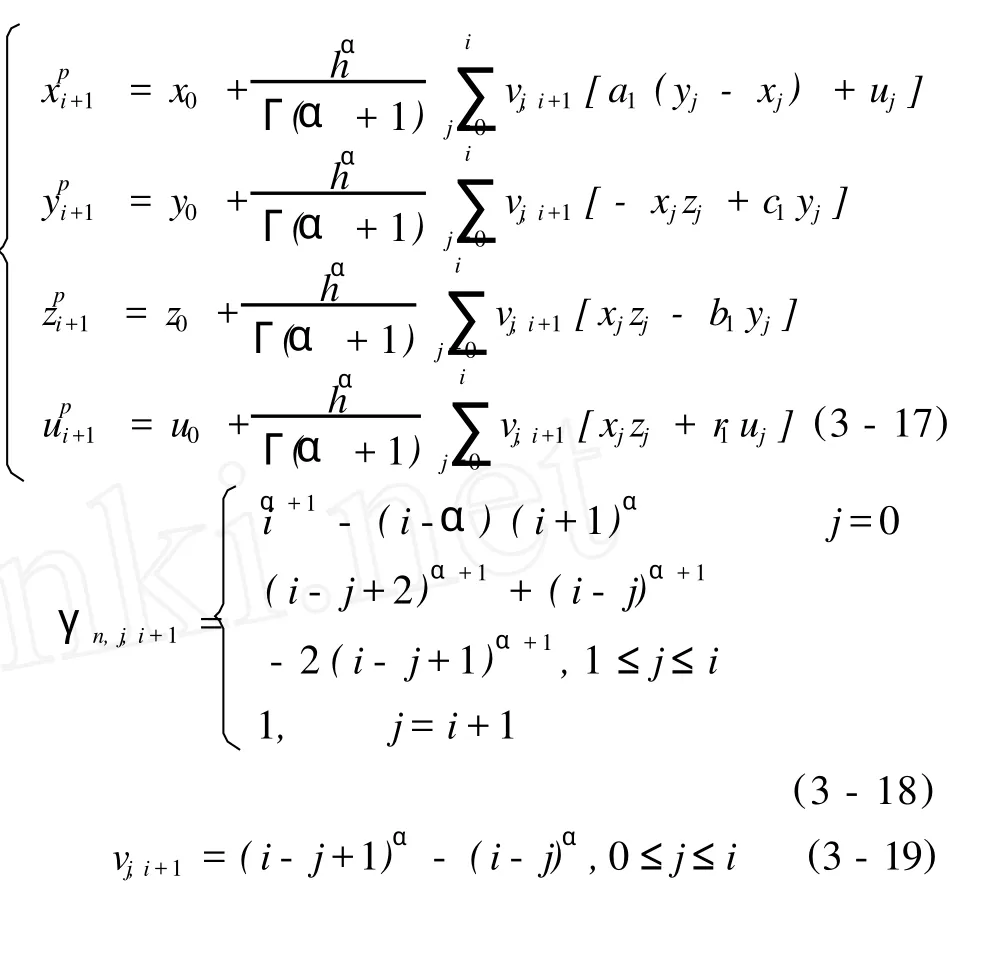
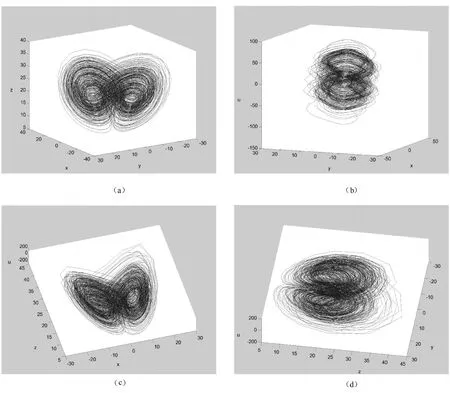
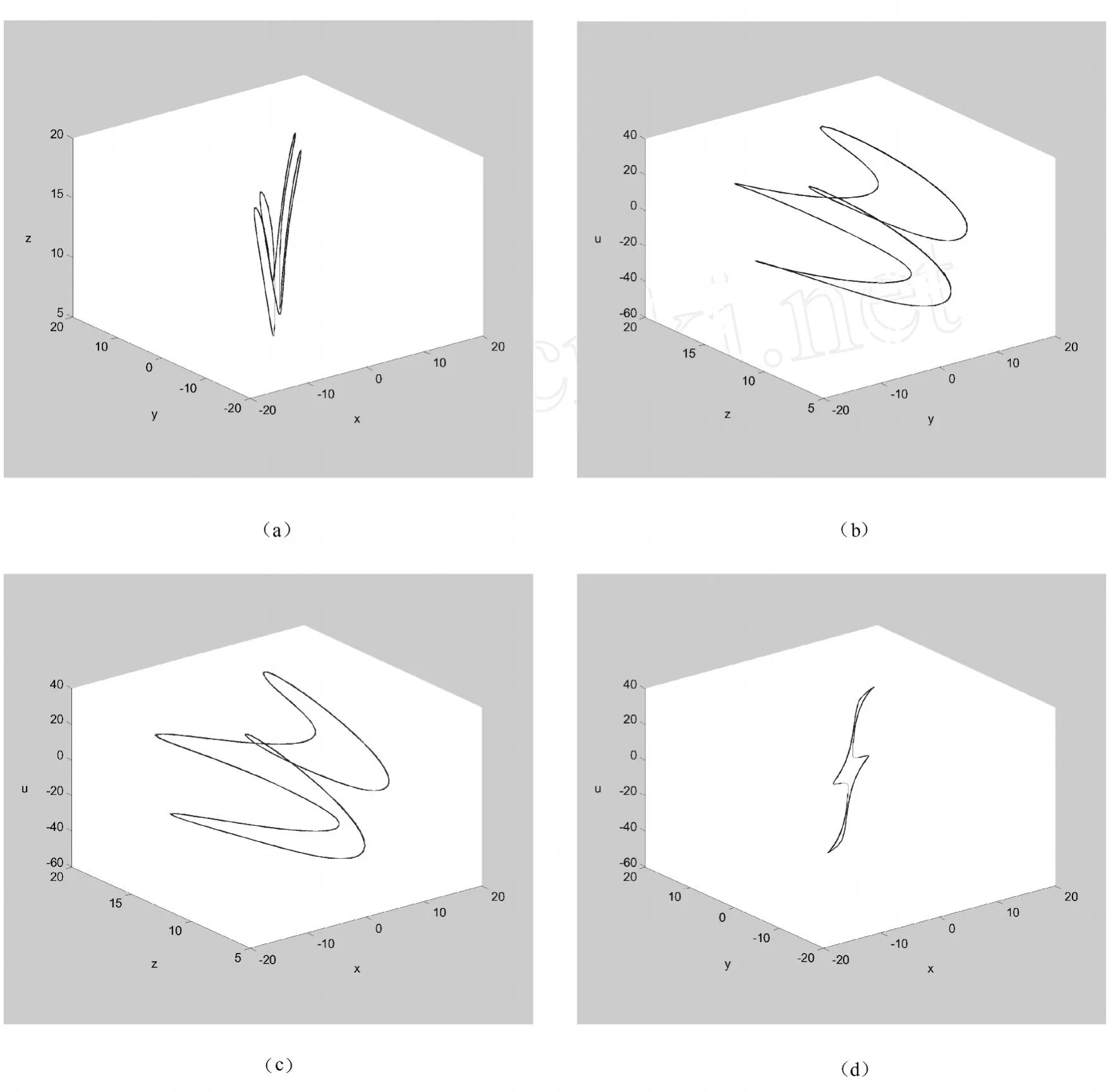
3 数值模拟
4 结论
