层次分析法在高校仪器设备招标评标中的应用①

宋 云 王新玲 王 鹏

(华北科技学院 资产管理处,北京 东燕郊 101601)

层次分析法在高校仪器设备招标评标中的应用①

宋 云②王新玲 王 鹏

(华北科技学院 资产管理处,北京 东燕郊 101601)

本文运用层次分析法对影响高校仪器设备招标评标评标的各种指标分层排序,组成一个有序的递阶层次结构,通过计算确定其权重,将定性和定量相结合提供一种科学的方法,从而减少人为因素的影响,体现“公开、公平、公正”的竞争原则。

层次分析法;高校;设备;招投标

近年来,随着高校招生规模不断扩大,在校学生人数陡增。为保证教学质量,国家及学校增加了教学仪器设备经费的投入,高校仪器设备采购任务也日益趋繁重。由于该工作是一项具体的,政策性强,涉及面广,技术知识要求高,多因素复杂的系统工程[1-4];采购工作在遵循市场经济活动的原则下,按国家的政策法规和学校的规定以竞争方式通过招标、投标、开标、评标和定标等一系列步骤来确定中标单位并签订合同,从而减少人为因素的影响,体现出公开、公平、公正和诚信与竞争的原则。但由于评标方法的不同,有时会得出不同的中标者。

层次分析法是对复杂问题做出决策的一种简明有效的方法[5]。将层次分析法用在招标评标工作中,在一定程度上满足了这种需要。它把定性分析与定量分析相结合,根据问题的总目标,以系统的观点,把问题分解成若干因素,并按其支配关系构成递阶层次结构模型,然后应用两两比较的方法确定决策方案之间的相对重要性,从而获得满意的决策。

1 层次分析法计算模型

1.1 确定评标条件,建立层次结构

根据某高校在采购仪器中的需要考虑的因素,按照招标文件的要求将从 4个角度 16个要素进行评价,现有 3个公司参与招投标竞争。建设一个层次结构模型如图 1所示。

1.2 判断矩阵构造

评标指标的权重是评价评标指标相对重要性的定量表示。首先,构造判断矩阵,其元素是对上层中某元素而言,将本层次中各支配元素两两比较。比较采用 1-9标度法[5]将其相对重要程度赋予一定数值而构造的。通过请有关专家对各影响因素的重要性予以量化,构成如下两两比较判断矩阵。

以总目标O层为准则,A层次各元素的两两比较判断矩阵OA为

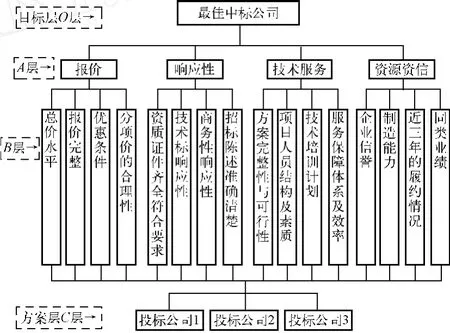
图 1 评标条件层次结构模型

类似地,以A层各指标为准则,B层各元素的两两比较判断矩阵A1B、A2B、A3B、A4B分别为

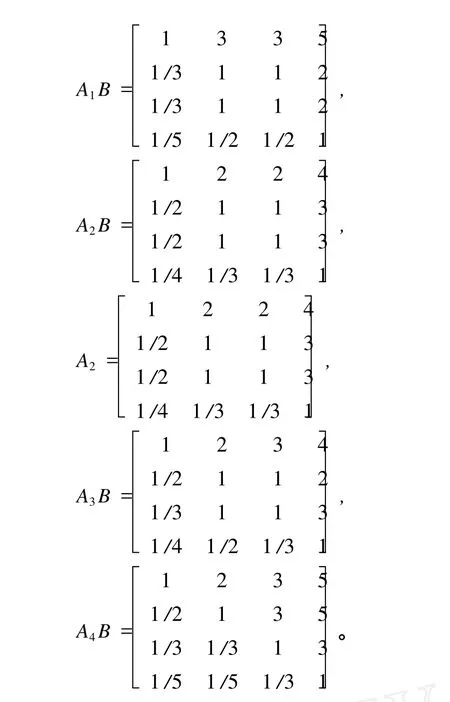
以B层各指标为准则,C次各投标公司的两两比较判断矩阵B1C、B2C、B3C、B4C、B5C、B6C、B7C、B8C、B9C、B10C、B11C、B12C、B13C、B14C、B15C、B16C分别为

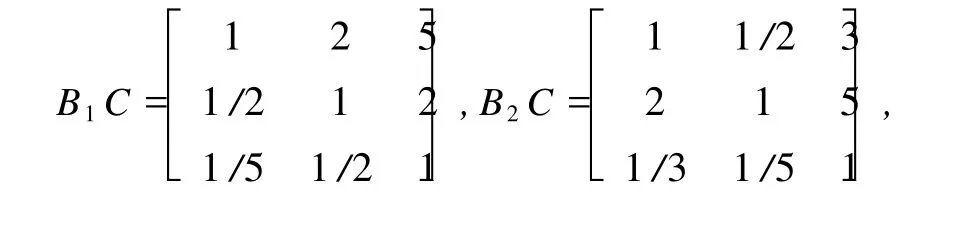
2 各判断矩阵一致性检验

根据判断矩阵随机一致性比率CR确定其一致性,当CR<0.1时认为判断矩阵具有一致性,否则需要调整矩阵元素的值。随机一致性比率CR由下式计算

表 1 平均随机一致性指标

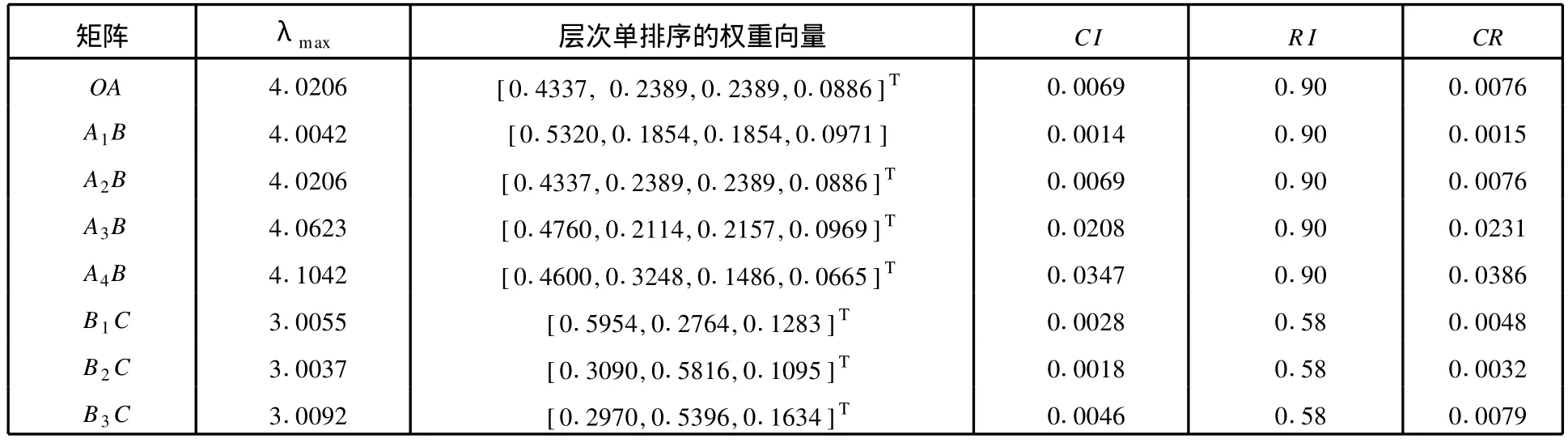
表 2 各矩阵的最大特征值λmax、相应的特征向量、CI和 CR

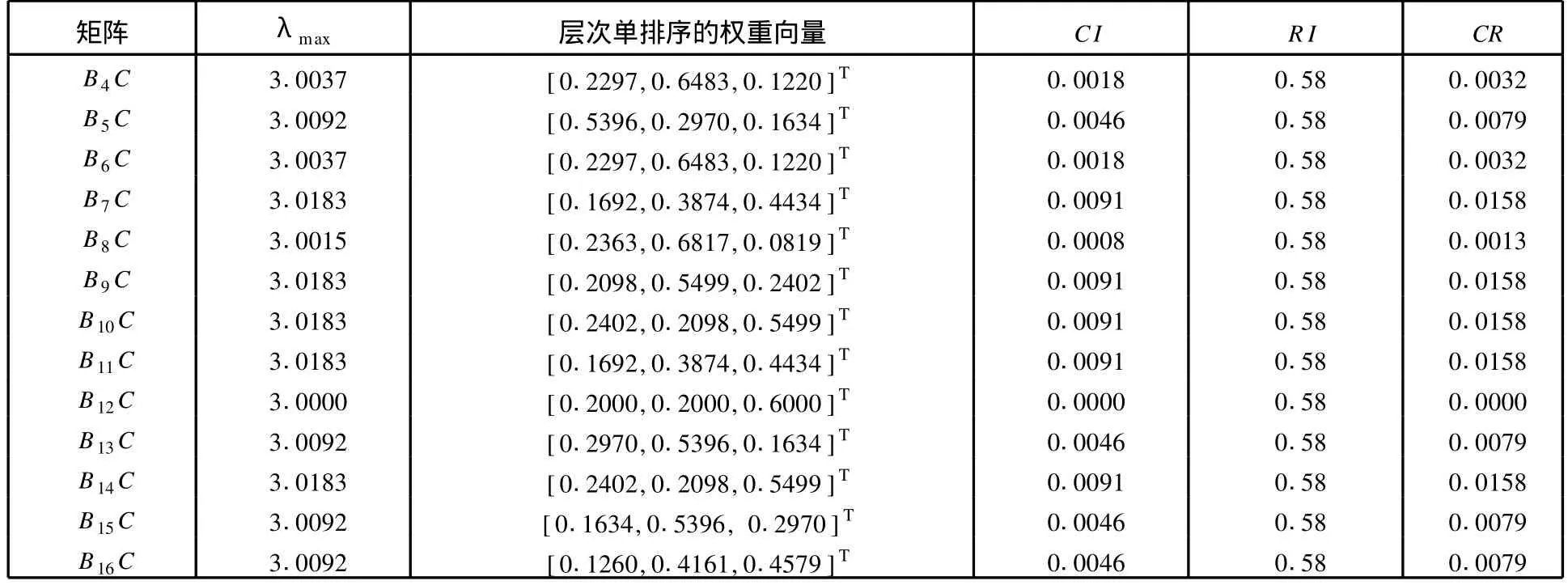
续表

式中,R I—平均随机一致性指标,与判断矩阵的阶数p有关,相应值列于表 1[5];

CI—判断矩阵一致性指标,与最大特征值λmax有关,由下式计算

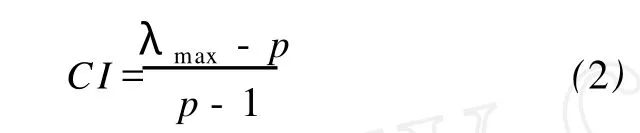
计算结果表明,所有 21个层次单排序的CR值都小于 0.1,均符合一致性要求。

3 层次总排序的一致性检验

如果层次结构的总层次数n≥3时,除了进行层次单排序进行一致性检验外,还需要对层次总排序进行一致性检验,各层次总目标的一致性比例小于 0.1。其中第k层次对总目标的一致性比例CRk为

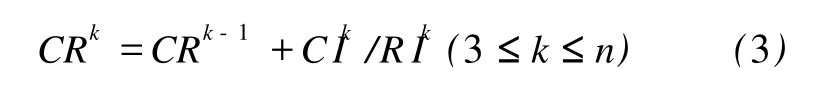
式中,CIk—第k层对总目标的一致性检验指标;

R Ik—第k层对总目标的随机一致性指标。

CIk和R Ik分别由下式计算

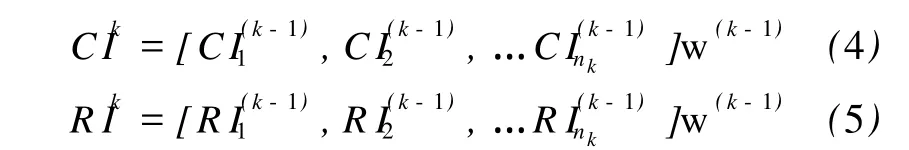
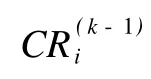
w(k-1)—第k-1层对总目标的总排序向量,由下式计算

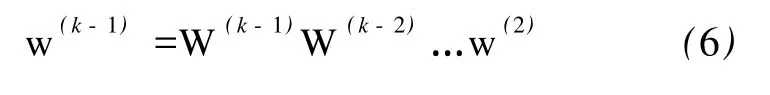
式中

w(2)—第 2层(即A层)各指标对总目标的排序,即矩阵OA最大特征值对应的特征向量

W(k-1)—第k-1层各元素对上一层第k-2层各指标权向量构成的矩阵

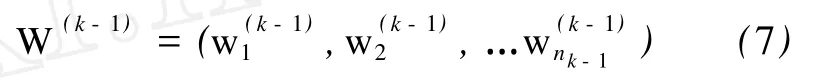
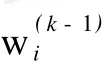
由表 2计算结果,得到第 3层(B层)对第2层(A层)各指标的排序矩阵 W(3)及第 4层(C层)次对第 3层(B层)各指标的排序矩阵W(4)。

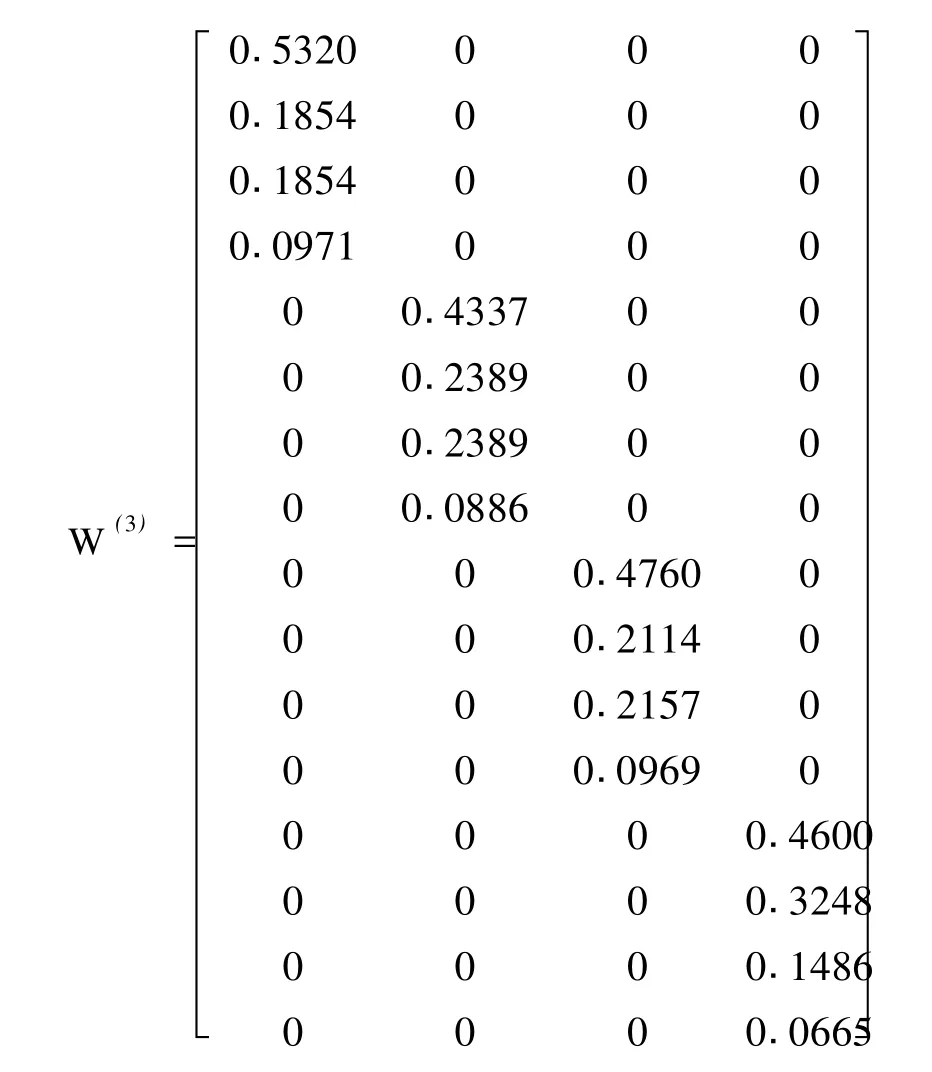
由公式(6),第B层各指标对总目标的排序为[0.2307,0.0804,0.0804,0.0421,0.1036,0.0571,0.0571,0.0212,0.1137,0.0505,0.0515,0.0231,0.0408,0.0288,0.0132,0.0059]T。

方案C层对总目标的排序为 [0.35067,0.42081,0.22852]T,由此说明,三个投标公司对总目标的优劣顺序为公司 2、公司 1、公司 3,其中公司 2为最优。

第三层对总目标的一致性指标CI=0.0103,相应的随机一致性指标R I=0.9000,一致性比例CR=0.0191<0.1,符合满意一致性要求。

第四层对总目标的一致性指标CI=0.0049,相应的随机一致性指标RI=0.5800,一致性比例CR=0.0274<0.1,符合满意一致性要求。

4 结语

应用层次分析法通过构造判断矩阵将评标指标量化,便于实现计算机上的运算操作,为更好地确定最终中标者提供了科学的依据,减少了人际关系的干扰,增加了经费支出透明度,体现了评标的公正、合理,是一种较为有效实用的评标办法。具有普遍推广的价值。

[1]国家计委政策法规司 .招投标法释义[M].北京:中国计划出版社,1999

[2]张国兴,胡绍兰 .运用层次分析法进行招标评标[J].基建优化,1997,18(1):23-27

[3]段爱玲,王高平,李永刚 .层次分析法在设备采购评标中的应用[J].计算机与信息技术,2005(12):39-41

[4]郑勇强,陈伯望 .模糊层次分析法在工程招投标中的应用 .湖南城市学院学报(自然科学版),2005,14(1):11-14

[5]赵焕臣,许树柏 .层次分析法—一种简易的新决策方法[M].北京:科学出版社,1986

Application of the Analytic Hierarchy Process on the Equipment Tender Evaluation at the College

SONG Yun,WANG Xinling,WANG Peng

(AssetManagementDepar tment,North China Institute of Science and Technology,Yanjiao Beijing-East 101601)

The procurement of the equipment is a policy-oriented,wide range,high technical knowledge and many complicated factors systems engineering.This paper applies analytic hierarchy process(AHP)to hierarchical order various indicators on the impact of evaluation and forms an orderly hierarchical structure.By calculates and deter mines the weight,provides a qualitative and quantitative scientific method.Thereby the influence of human factors is reduced,which reflects an open,fair and just principle of competition.

Analytic Hierarchy Process;College;Equipment;Tender and bid

G647

A

1672-7169(2010)04-0093-04

2010-07-15

宋云(1968-),女,山东泰安人,大学毕业,华北科技学院资产管理处工作人员。