一种高精度模糊控制方法①

杨文光

(华北科技学院 基础部,北京东燕郊 101601)

一种高精度模糊控制方法①

杨文光②

(华北科技学院 基础部,北京东燕郊 101601)

本文介绍了基于矩形邻域的泰勒二元一次展开式的改进控制方法,并将其应用到二阶系统的控制仿真实验中。仿真结果表明该方法具有响应快,无超调,稳态误差极小等优点,在要求高精度的复杂、时变、非线性的工程实践中具有很好的应用前景。

泰勒展开式;矩形邻域;稳态误差;插值;仿真

0 引言

由于常规模糊控制的量化取整和调节死区的存在,得到的控制仿真曲线一般都有稳态误差与振颤现象,为此有许多学者着手于提高模糊控制系统稳态性能的研究,并且已经取得了很多成果。李洪兴教授在文献[1]中提出,模糊控制本质上是一种插值控制,为我们研究模糊控制性能的提高提供了崭新的思路。章卫国等人则在模糊数模型基础上开展了具体的插值方法的分析研究,先后在文献[2]、[3]中提出了基于矩形域的二元插值法,基于矩形域的一次、二次样条的曲面磨光法,以及泰勒二元函数的一次展开式法,这些方法显著提高了模糊控制系统的性能,克服了常规模糊控制器存在的固有缺陷,并且具有简单易行和很好的普适性。但具体分析原文中的泰勒二元函数的一次展开式,由于只取到一阶而舍弃了很多项,故在要求精度较高的控制场合,则有些粗糙,本文拟使用泰勒二元函数一次展开式法,通过矩形邻域泰勒展开得到近似程度较高的公式,使其满足模糊控制的插值性,并进行仿真实验。

模糊控制器建立了控制输入与控制输出之间的映射关系。对于多输入单输出模糊控制系统,随着某个输入变量取值的增大而其他的输入变量取值不变时,为了跟踪参考输入,模糊控制器的输出就会做出相应的调整,表现为不减趋势。这种性质就是模糊控制器所具有的单调性。使用泰勒展开式得到的模糊控制器,较好的满足了单调性,在保证插值的前提下,这种映射关系非常容易建立。以下开始基于泰勒展开式的双输入单输出模糊控制器的建立。

1 矩形邻域泰勒展开式

设X=[a,b]⊂R,Y=[c,d]⊂R分别是输入变量x和y的论域,Z=[e,f]⊂R为输出变量z的论域。给定双输入单输出模糊控制规则库：

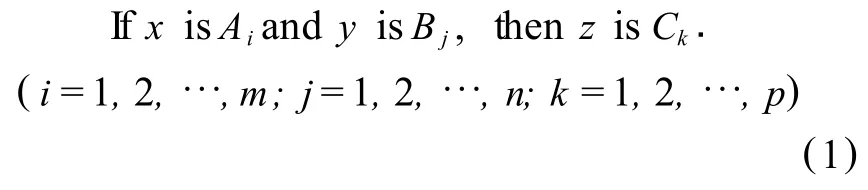
设xi分别为Ai的峰点,yj分别为Bj的峰点,zk分别为Ck的峰点,而Ai,Bj,Ck分别为论域X,Y, Z上的正规三角形全交迭的模糊集(i=1,2,…, m;j=1,2,…,n;k=1,2,…,p)。根据专家经验,对应典型的控制输入数据对(x,y),就有典型的输出z,从而由插值机理就确定了输入事实与输出结论之间的映射关系：f：(x,y)|→z,x∈X,y∈Y,z∈Z。

在上面得到的模糊控制规则的基础上,很容易由两个输入变量确定一个输入平面。输入平面内许多峰点搭配组成网点,彼此相邻网点构成矩形。设某个矩形邻域V的四个顶点分别为(xi, yj),(xi+1,yj),(xi,yj+1),(xi+1,yj+1)(见图1)。假设相对已知输入事实的输出控制策略是明确的,那么在f作用下显然有

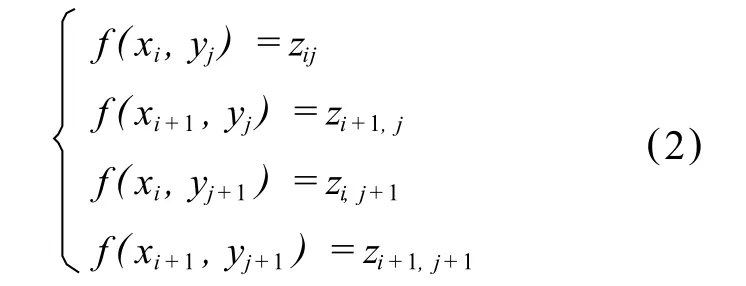
其中zij,zi+1,j,zi,j+1,zi+1,j+1分别对应某个zk,k=1,2,…,p。

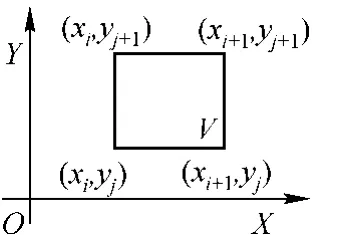
图1 矩形邻域

2 仿真实验

通常的工业过程可以等效成二阶系统加上一些典型的非线性环节,如死区、饱和、纯延迟等环节,设某个带有0.1秒纯延迟系统的传递函数为

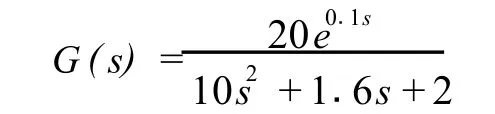
设误差E、误差变化CE及控制量U的论域均选取为

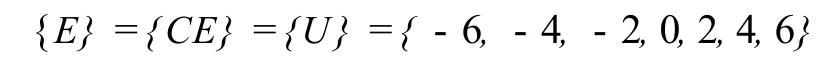
则在全论域内的控制规则按照解析表达式概括为

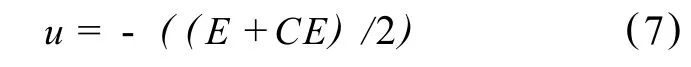
式中E、CE及U均为经过量化的模糊变量,但u未经取整运算。在以下实验中,取ke=10,kd=1/2, ku=100,且E=ke×e,CE=kd×ce,U=ku×u。

情形1 若采样时间T=5s,采样步长h= 0.01s,初始状态选取为x1(0)=0,x2(0)=0,参考输入为r(t)=2.5cost+1.5,则在⑹式作用下得到的控制仿真曲线非常理想(见图2),如果排除0.1s的纯延迟时间,则上升时间与调整时间的总时长仅约为0.4s,图3给出了误差绝对值变化曲线,系统响应非常好,稳态误差极小。

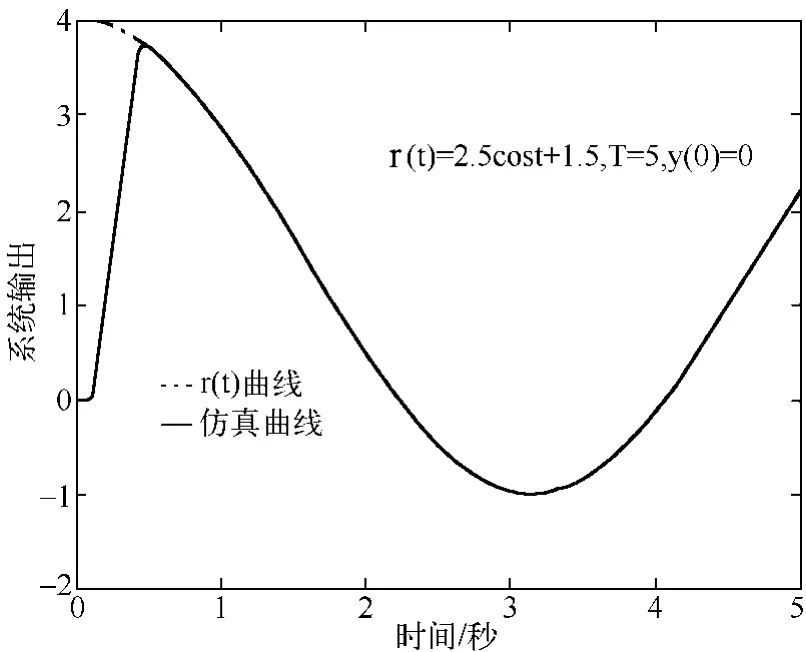
图2 r(t)=2.5cost+1.5的仿真曲线

图3 参考r(t)=2.5cost+1.5输出的误差绝对值曲线

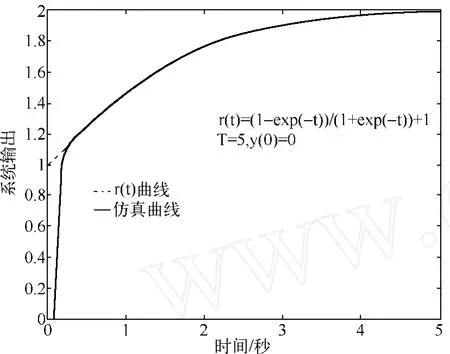
图4 r(t)=1的仿真曲线

3 结论

本文在泰勒二元函数一阶展开式的基础上附加上了一个修正项,在该公式控制作用下使得落在输入平面某个矩形网格内的输入事实有相应的控制输出,得到非常理想的控制效果,基本上消除了稳态误差,并且响应快,无超调。该方法在要求高精度的工程实践中具有很好的应用前景。

图5 参考r(t)+1输出的误差绝对值曲线

[1] 李洪兴.Fuzzy控制的数学本质与一类高精度Fuzzy控制器的设计[J].控制理论与应用, 1997,14(6)：868-876

[2] 章卫国,薛璞,段富海.一种高精度模糊控制系统的设计方法[J].测控技术,1997,16(2)：22-24

[3] 章卫国,薛璞,杨向忠.一种高精度模糊控制器[J].自动化与仪器仪表,1997(73)：35-39

[4] 章卫国,杨向忠.模糊控制理论与应用[M].西安：西北工业大学出版社,2000

[5] 易武,李力争.模糊控制器的一种加权算法[J].控制与决策,1992,7(5)：382-385

[6] 李士勇编著.模糊控制、神经控制和智能控制论[M].哈尔滨：哈尔滨工业大学出版社,1998

[7] 杨文光,赵海良.基于样条插值的模糊控制算法[J].模糊系统与数学,2009,23(3)：152 -157

A Highly-accurate Fuzzy ControlM ethod

YANG W enguang

(Depar tment ofBasic Course,North China Institute of Science and Technology,Yanjiao Beijing-East 101601)

This paper introduces the improvementof Taylor's expansion of first-order based on rectangular domain.And themethod was applied to control a second system in simulation exper iment.The result of the improvementmethod indicates the requirement of control is quick,and no overshoot,the steady state error can be negligible.So the improved method has a good application in the future.

Taylor's expansion;Rectangular domain;Error;Interpolation;Simulation

TP273.+4

A

1672-7169(2010)04-0090-03

2010-08-21

杨文光(1981-),男,河北涞水人,硕士,华北科技学院基础部教师,研究方向：模糊控制与神经网络。