条件(PA)对幺半群的刻画①

2010-12-26许军

华北科技学院学报 2010年4期

关键词：条件

许军

(酒泉职业技术学院,甘肃酒泉 735000)

条件(PA)对幺半群的刻画①

许军②

(酒泉职业技术学院,甘肃酒泉 735000)

利用条件(PA)刻画了左可消幺半群,给出了一类特殊幺半群的S-系范畴特征.关键词：条件(P);条件(PA);左可消

0 引言

除特别声明外,本文中总是以S表示幺半群,所用其他符号均同文[1].

相应于R-模范畴中的平坦性概念,在S-系范畴中有强平坦、平坦、弱平坦、条件(P)、条件(E)等不同概念.称左S-系A满足条件(P)[2],如果sa=s′a′(s,s′∈S,a,a′∈A),则存在a″∈A, u,v∈S,使得su=s′v,a=ua″,a′=va″.称左S-系A满足条件(E)[2],如果对任意s,t∈S,任意a∈A,若sa=ta,则存在a′∈A,u∈S,使得su=tu,a= u a′.称左S-系A是弱平坦的[2],如果对于S的任意右理想I,映射I⊗A→S⊗A是单的.称左S -系A是主弱平坦的[2],如果对于S的任意主右理想I,映射I⊗A→S⊗A是单的.设A、B分别为右、左S-系,称B满足条件(PA)[3],对于任意a,a′∈A,b,b′∈B,若在A⊗B中有a⊗b=a′⊗b′,则存在b″∈B,x,y∈S,使得ax=a′,b=x b″, b′=y b″.称S是右PP幺半群[2],如果S的任意主右理想是投射的.右S-系A的相关定义可对偶得到.

设I是S的左理想,且I≠S,x,y,z是三个符号,令(S,x)={(s,x)∣s∈S},(S,y)={(s,y)∣s∈S}, (I,z)={(s,z)∣s∈I}.构造A(I)=(I,z)∪{(s,x)∣s∈S-I}{(s,y)∣s∈S-I},定义S在A(I)上的左作用为

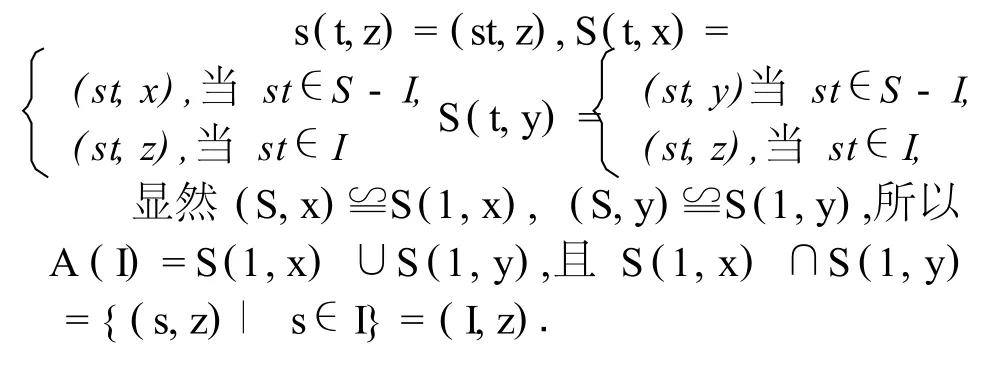
1 几个引理

引理1.1[2]设A,B分别是右左S-系,a,a′

2 主要结果

定理2.1 所有S-系满足条件(PA)当且仅当S是群.

定理2.2 对于幺半群S,以下条件等价：(1)所有满足条件(E)的S-系满足条件(PA); (2)所有满足条件(E)的S-系是平坦的;(3)所有满足条件(E)的S-系是投射的;(4)所有满足条件(E)的S-系是自由的;(5)S是群.

定理2.3对于幺半群S,以下三条等价：(1)S是左可消幺半群;(2)S是右PP的,且任意平坦S-系满足条件(PA);(3)S是右PP的,且任意弱平坦S-系满足条件(PA).

3 定理的证明

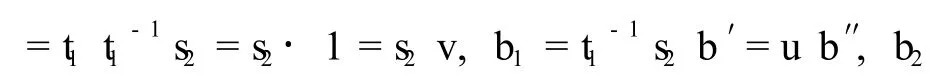
此等式组的个数比(＊)少2,所以可用数学归纳法完成证明.

⇒)设所有S-系满足条件(PA),则所有S-系满足条件(P).假定L是S的真左理想,构造S -系A(L)=S(1,x)∪S(1,y).因为S(1,x)∩S (1,y)≠Φ,S(1,x)≠S(1,y),由命题知有限生成的S-系A若满足条件(P),则A是有限个循环子系的不交并即得矛盾.矛盾说明S没有真左理想,所以S是群

定理2.2证明：(4)⇒(3)⇒(2)⇒(1)显然.

(1)⇒(5)设I是S的真左理想,则A(I)满足条件(E),由条件知,A(I)满足条件(P),当然满足条件(PA),矛盾,因此,S是群.

(5)⇒(4)设S是群,则易证所有左S-系都是循环子系的不交并,若B是满足条件(E)的S-系,则B≌S,因此,满足条件(E)的S-系是自由的.

定理2.3的证明：(1)⇒(3)当S是左可消幺半群时,显然是右PP的,设A是弱平坦S-系,a,a′∈A,x,y∈S,满足xa=ya′.则在S⊗A中有x⊗a=y⊗a′,由A的弱平坦性可知在(xS∪yS)⊗A中有x⊗a=y⊗a′,所以存在x1,…xn∈(xS∪yS),a2,…an∈A,u1,v1,…,un,vn∈S,使得

令z1=x,zi=xi-1vi-1,i=2,…,n+1.显然存在k={1,2,…,n+1},使得z=zk∈(xS∩yS),令a″=ak∈A,则利用上述等式组计算可知xa=ya′= z1a=zn+1a′=zkak=zka″=za″.因为xa=za″=xsa″,则在S⊗A中有x⊗a=x⊗sa″,由引理2.1可知,存在c1…,cn∈A,w2,…,wn∈S,s1,t1…sn,tn∈S,使得

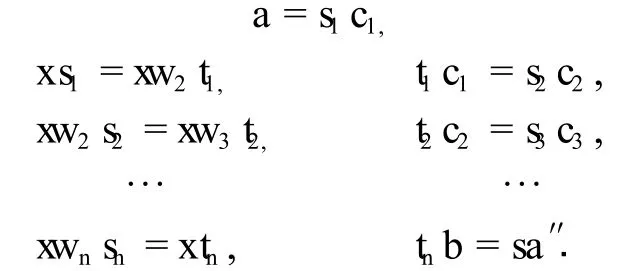
因为S是右PSF的,所以xS是强平坦的,自然满足条件(E),则对等式xs1=xw2t1,存在v∈xS,p∈S,使得x=vp,ps1=pw2t1,而v=xq,这里q∈S.所以有x=xqp,s1qp=w2t1qp,这说明x是左半可消元.因此,存在h1∈S,使得x=xh1,h1s1=h1w2t1,由x的左半可消性知,存在h2∈S,使得x= xh2,h2h1w2s2=h2h1w3t2.令h′=h2h1,则x=xh′, h′s1=h′w2t1,

h′w2s2=h′w3t2,利用数学归纳法可以证明存在h∈S,x=xh,hs1=hw2t1,hwnsn=htn,hwisi= hwi+1ti,i=2,…,n-1.因此,ha=hs1c1=hw2t1c1=h w2s2c2=…=hwnsncn=htncn=hsa″.

同理,由ya′=za″=yta″知,存在g∈S,使得y =yg,ga′=gta″.

令m1=hs,n1=gt,则ha=m1a″,ga′=n1a″,且xm1=xhs=xs=yt=ygt=yn1,由S的左可消性可知,h=1=g,所以a=m1a″,a′=n1a″,因此A满足条件(P),自然满足条件(PA).

(3)⇒(2)显然

(2)⇒(1)由引理2.4知,E(S)=1,设r,x,y∈S满足条件rx=ry,因S是右PP的,所以存在e∈E(S),使得r=re,且若rs=rt,则es=et,特别地有ex=ey,但e=1,所以x=y,这说明S是左可消的.

[1] J.M.Howie.An Introduction to Semigroup Theroy [M].Academic Press,1976

[2] 刘仲奎.半群的S-系理论[M].科学出版社,1998

[3] 刘仲奎.强忠实右S-系[J].数学杂志,1995, 15(4)：,429-435

Describe theM onoids with the Condition(PA)

XU Jun

(Jiuquan Vocational and Technical College,Jiuquan Gansu 735000)

we describe the left el iminationmonoidiwith the condition(PA),and get a characterization of S-actson some specialmonoids.