基于遗传算法的路由选择问题的研究①

申彦春

(唐山学院信息工程系,河北唐山 063000)

基于遗传算法的路由选择问题的研究①

申彦春②

(唐山学院信息工程系,河北唐山 063000)

针对多目标优化问题,应用免疫遗传算法的基本思想,提出了一种求解满足带宽-时延约束多组播路径问题的两层遗传算法。在算法中设计了一种基于节点连接路径的具有树状结构的染色体表示方法及可以实现树状染色体交叉和变异的算子。数值实验结果表明,文中提出的算法可以有效找到多组播路由问题的优化解。

多组播路由问题;免疫理论;遗传算法;QoS路由

0 引言

遗传算法是模拟自然界生物优胜劣汰、适者生存的法则进行科学研究的一种手段。在遗传算法中,个体的适应度是判断个体生存能力的唯一标准。通过对群体中的个体进行遗传操作,实现群体内部结构的重组,进而使群体的性能逐渐得到优化,最终接近最优解。然而遗传算法又是一种新型的优化技术,它今后的发展还有许多工作需要去不断充实和提高。因此以遗传算法为主要研究对象,来求解实际问题是很有意义的[1]。

1 QoS路由问题

目前,在Internet中大部分是“尽力而为”(best-effort)的路由协议,并且采用“最短路径”的寻径策略,因而无法满足多媒体信息传输的要求。从网络用户的角度来看,基于QoS(Quality of Service,服务质量)的路由算法首先应保证满足用户的QoS请求,即寻找一条满足各种条件限制的从源节点到目的节点的传输路径。从服务提供商的角度来看,基于QoS的路由算法应能最优化地使用网络资源[2]。

网络提供给用户的QoS是由网络的各种参数决定的。因此,RFC 2216将QoS定义为：由可用带宽、延时、延时抖动和包丢失率等参数描述的分组传输特性。网络要满足用户的服务质量要求,就必须满足用户要求的QoS参数。

一般地,网络的拓扑结构和链路状态信息可以抽象为一个赋权图(G=V,E),其中：

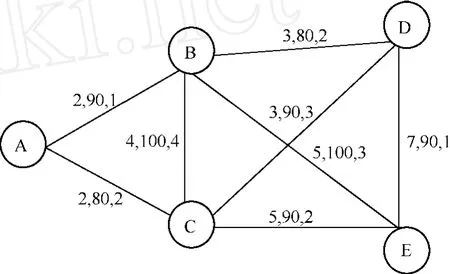
图1 QoS路由选择问题的网络拓扑图

图的顶点表示网络节点,图的边表示网络链路,V=(V1,V2,…,Vn)是代表路由器的所有交换节点的集合,E=(E1,E2,…En)是所有连接路由器的链路的集合。QoS路由选择就是在图1中查找满足网络QoS要求的路由,而QoS路由涉及的度量参数一般包括：带宽、时延和代价等。

2 基于免疫遗传算法的QoS路由选择问题

2.1 QoS路由选择问题的数学模型

为了更好地分析问题和解决问题,为QoS路由选择问题建立一个数学模型。在图1中,A、B、C、D、E表示路由,路由之间的连线表示相连的两个路由之间是通路,每条链路用(cost,width,delay)表示,分别代表这条通路的费用、带宽和时延。

根据上面论述的QoS路由选择问题应考虑的因素和影响,可以认为带宽、时延和费用问题是影响有关QoS路由选择问题的关键因素,但是如果在设计具体的路由算法时考虑所有因素,算法势必太复杂而不能实际应用,所以应该针对不同的实际需要设计相应的算法,处理不同的约束条件。通过进一步的分析,可以知道通常在QoS组播路由选择时,由于延时和带宽是作为实时多媒体传输必须保证的基本条件,而费用作为评价网络使用效率的重要因素,所以可以得到以上条件下的约束条件：

对任意一条链路来说(a,b),D(a,b)表示通过该链路产生的延时,B(a,b)表示该链路的可用带宽,C(a,b)表示该通信过程中所需的费用。设u,v之间的路径的延时为

从上述QoS路由选择问题的约束条件可以得到QoS路由选择问题的数学模型,为：

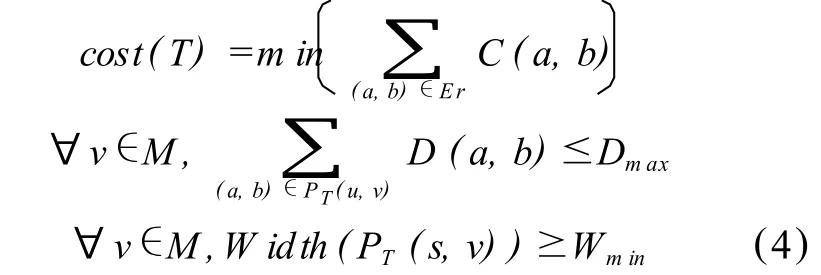
2.2 基于免疫遗传算法QoS路由选择问题解决方案

根据遗传算法的基本原理和免疫算法的核心思想,可以得到解决该问题的流程图,如图2所示：

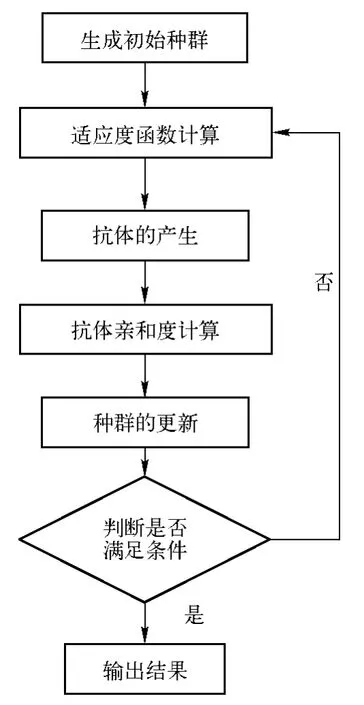
图2 基于免疫遗传算法的QoS路由选择问题流程图

下面对流程图中的每一个步骤进行详细介绍。

2.3 生成初始种群

生成初始种群这一步需要通过三个小的步骤来完成,分别是对链路的编码、种群的初始化和链路的预处理。

1)编码

由于遗传算法不能直接处理解空间的解数据,因此必须通过编码将它们表示成遗传空间的基因型串结构数据。遗传算法将求解目标问题编码表示为“染色体”,在编码过程中,首先根据具体的路由拓扑图确定“染色体”的长度和各位所代表的含义,再通过二进制表示出来,即将原问题的解映射到位串空间,位串的每一位为0或1,以便在位串空间上进行遗传操作。

2)种群的初始化

由于遗传算法的群体型操作需要,必须为遗传操作准备一个由若干“染色体”组成的初始群体。初始群体的每个个体都是通过随机方法产生的。该种群代表优化问题的一些可行解的集合,一般而言初始种群的素质较差,算法的任务是从这一初始种群出发,模拟进化过程,择优去劣,最后找出优秀的群体和个体。

3)对链路的预处理

这一步主要是用于除去不满足带宽约束条件和延时约束条件的链路。通过设置最小带宽约束条件和最大延时约束条件,对每一条链路进行检查,来确保链路符合带宽约束条件和延时约束条件的要求。

2.4 适应度函数的计算

适应度函数为

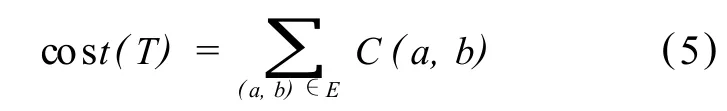
式中,C(a,b)表示通信过程中经过的链路所需的费用。适应度函数值越小,即表明该通信过程中所需要的费用越小,这样的结果是我们所期望得到的。

2.5 抗体的产生

在抗体的产生这一步骤中,共有三项工作需要完成,即选择、交叉和变异。

1)选择

在选择这一步骤中,将按照一定的原则选出一些的个体遗传到子代。这个原则就是根据各个个体的选择概率进行选择操作,其中各个个体选择概率与其适应度函数成比例。选择概率为

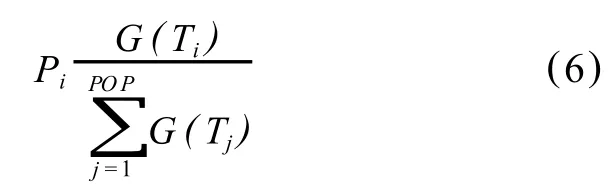
2)交叉

交叉是指选择两个个体,并在个体中选择一个或多个交叉点,通过操作使这两个交叉点之后的信息进行交换。通过交换操作可以得到新一代个体,这些新个体组合了其父辈个体的特性。交换操作体现了信息交换的思想。

3)变异

变异是首先在群体中随机选择一个个体,对其以一定的概率随机地改变串结构数据中某个值。这样可以为新个体的产生提供机会。

2.6 抗体亲和度的计算

抗体亲和度aymv表示抗体m和抗体w之间的亲和力,其公式表示为

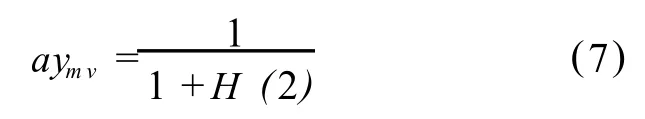
其中,H(2)表示抗体m和抗体w的平均信息量。

2.7 种群的更新

根据免疫遗传的原理,个体适应度越大,则选择的概率越大(促进),保证了进化群体中保留适应值大的个体(加速算法的收敛);个体浓度越大,则选择的概率越小(抑制),保证了进化群体中个体的多样性,避免“早熟”[3]。

所以根据综合抗体浓度和适应度函数来对抗体进行促进和抑制。

式中N表示种群中个体的数量,λ表示种群相似度阈值。

综合后的评价标准聚合适应度,其表达式为

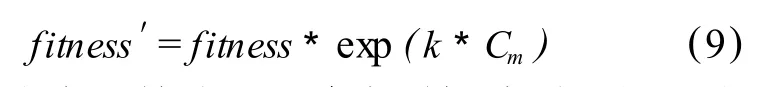
通过这个函数就可以决定对抗体采取促进或抑制的措施,从而使种群得到更新。

3 结果分析

根据该算法各部分程序与设置的参数的关系,可以确定MATLAB程序中的参数值,生成的初始种群个体数量Popsize=50,编码长度xZomelength=9,其中numVar=8表示经过的路径,第九位表示适应度函数值或聚合适应度值;最大延时约束条件Dm=10,最小带宽约束条件Wm=100;交叉参数pc=0.3,变异参数pm=0.15;种群相似度阈值A0=0.03,抗体之间的亲和度阈值A= 0.9,在更新中产生的种群的个体数量P=10。

通过对所编写程序进行仿真运行和数据分析,要想判断这个算法是否起到一定的作用,需要从整体适应度函数和最优路径的选择情况两个方面来进行评价。因此,下面将就结合这两方面的仿真数据进行分析。

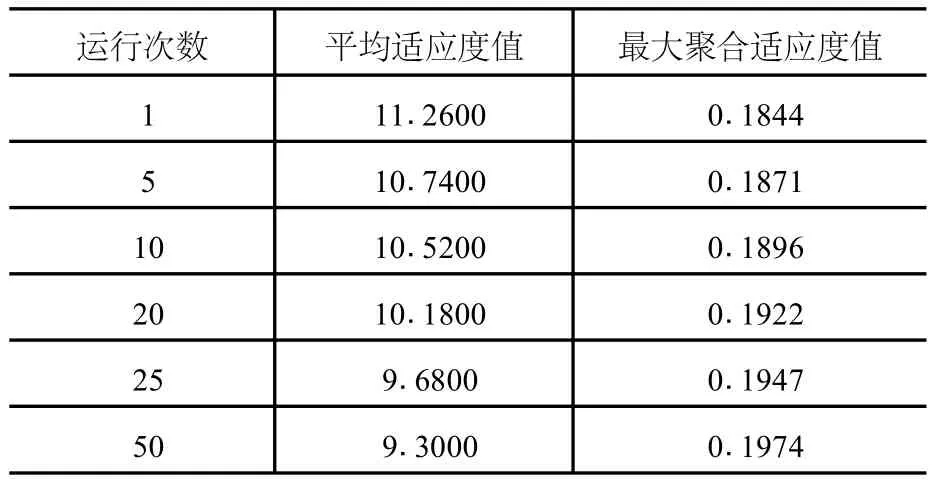
表1 整体适应度函数优化结果评价

从表1的优化结果可以看出,随着运行次数的增加,平均适应度函数值所呈现的趋势是逐渐减小,说明选择的个体所需费用越来越低;最大聚合适应度函数值所呈现的趋势是逐渐增加的,这说明选择个体的适应度越来越符合具体问题所要求的条件。同时可以看出如果对免疫遗传算法程序进行多次运行可以得到更好的效果。

表2中通过最优路径的出现次数和其在最终得到的种群中所占的比例来反映仿真实验的数据：

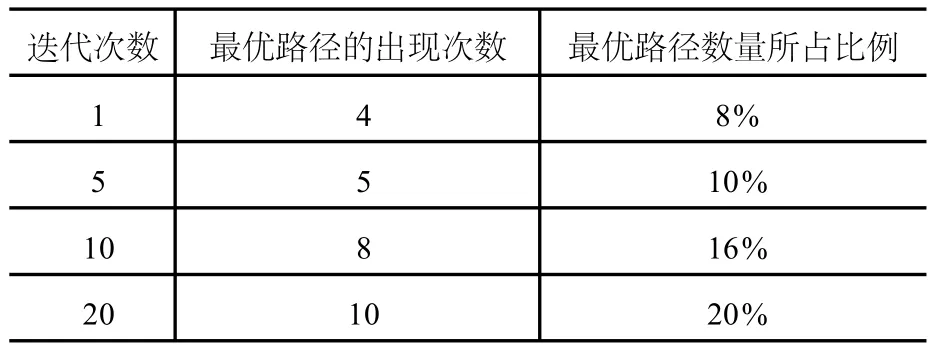
表2 算法最优路径的选择情况

通过上述仿真数据可以看出,上述数据所传递的信息是随着迭代次数的增加,在最终得到的种群中最优路径的出现次数是逐渐增多的,相应地其在种群中所占比例也是逐渐增大的,这符合根据免疫遗传算法特点推断得出的理想结果的要求[4]。

[1] 张安英.遗传算法在多目标优化中的应用研究[D].辽宁工程技术大学,2008

[2] 吴勇,郭京蕾,魏长华.遗传算法求解FDP问题[J].计算机工程与设计,2004(4)：561 -563

[3] 杨波,宋耀良.一种新的混沌遗传算法及其在多播路由选择中的应用[J].南京理工大学学报,2004,28(1)：29-33

[4] 高坚.基于免疫机制和遗传进化的网络组播路由优化算法[J].微电子学与计算机,2003, 20(8)：20-21

Routing problem based on genetic algorithm for

SHEN Yanchun

(Depar tment of Information Engineering,College of Tangshan,Tangshan Hebei 063000)

To solve the problem ofMulti-objective optimization,Thispaperproposed genetic algorithms to solve the problem,an algorithm with two genetic modules are represented.In the module of findingmulticast tree the codingwith tree-structured chromosome by connected nodes,and crossover and mutation operators are designed.The numerical simulation shows that it is efficient to search high quality solutions for the multiple-multicast routing problem.

multiple-multicast routing problem;Genetic algorithm; Immune theory;QoS routing

TP183

A

1672-7169(2010)04-0081-03

.2010-08-29

申彦春(1980-),男,河北唐山人,唐山学院讲师,主要研究方向为：信号处理,控制工程。