Gunther Jäger拓扑空间中的闭包算子和内部算子的研究①

韩元良

(华北科技学院 基础部,北京 东燕郊 101601)

Gunther Jäger拓扑空间中的闭包算子和内部算子的研究①

韩元良②

(华北科技学院 基础部,北京 东燕郊 101601)

本文首先分别定义了 Gunther Jäger拓扑空间上的闭包算子和内部算子,并考查了它们的性质;其次证明了它们 Gunther Jäger与拓扑之间的相互确定性

模糊集;Gunther Jäger拓扑空间;闭包算子;内部算子

1 预备知识

设X是非空集合,记X上的模糊集为A,B,C,…∈[0,1]X.这里假定读者已经了解模糊集理论和模糊拓扑理论的相关知识 .X上的模糊拓扑τ是X上的包含所有常值模糊集的一族模糊集,并且满足其上的任意两个元素的交集以及任意多个元素的并集仍是τ中的元素(Lowen[2]).

设A∈[0,1]X是模糊集,记FX(A):={B∈[0,1]X;B⊆A},并记A0:={x∈X;A(x)≥0}为A的支集,则FA0(A):={B∈[0,1]A;B⊆A}.若B∈FX(A),记B的伪补为〈AB,即〈AB(x):=A(x)-B(x),x∈X.基于此,下面给出Gunter Jäger拓扑(Gunter Jäger[1])的定义,另为方便起见,本文中将该拓扑简记为GJt.

定义 1 设A∈[0,1]X,称集族τ⊆FX(A)为定义在A上的拓扑,当且仅当满足以下条件:

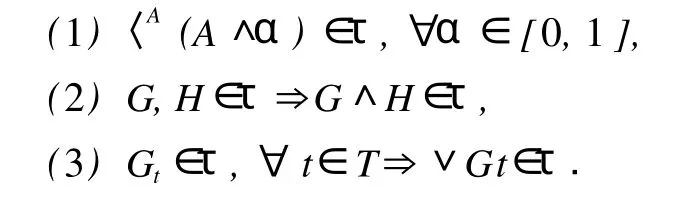
称(A,τ)是Gunter Jäger拓扑空间,也简记为GJts.τ中的任一元素称为τ-开集,则H∈FX(A)是τ-闭集当且仅当〈AH是τ-开集 .

2 Gunter Jäger拓扑空间上的闭包算子和内部算子

本节中,首先定义GJts上闭包和内部的概念,然后定义其上的闭包算子和内部算子,并分别研究它们的性质及它们与GJt之间的相互确定关系.

定义 2 设(A,τ)是GJts,B∈FX(A).分别

定义B的闭包和内部如下:

现在,可以利用闭包和内部的概念分别定义闭包算子和内部算子如下 .

定义 3 设(A,τ)是GJts,B∈FX(A).定义映射

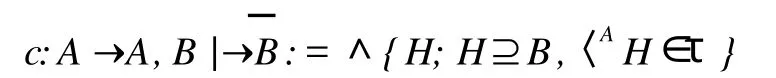
称c是定义在A上的闭包算子 .同样,定义映射

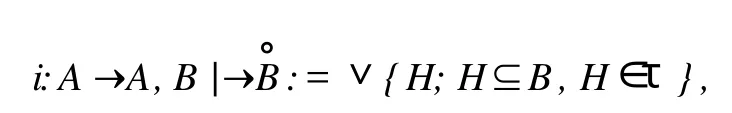
称i是定义在A上的内部算子 .

分别研究A上的闭包算子c和内部算子i,可得到定理 2和定理 3.

定理 2 设(A,τ)是GJts,c是闭包算子 .则算子c有如下性质:

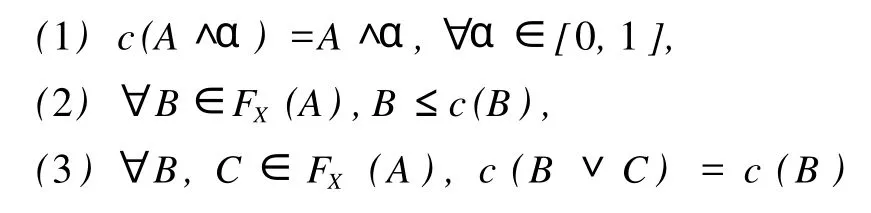
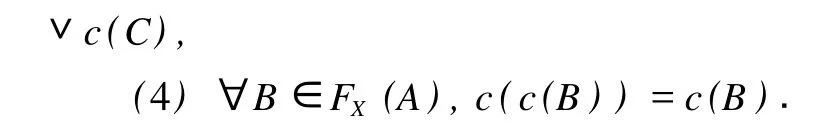
证明(1)由〈A(A∧α)∈τ知A∧α是τ-闭集 .则

c(A∧α)=∧{H;H⊇(A∧α),〈AH∈τ}=A∧α.

(2)由定义 3易知 .

(3)易知映射c是保序的 .因此,c(B∨C)≥c(B),c(B∨C)≥c(C),即c(B∨C)≥c(B)∨c(C).另一方面,,B≤c(B),c≤c(C)成立 .因此,(B∨C)≤c(B)∨c(C),则c(B∨C)≤c(B)∨c(C).综上知(3)式成立 .

(4)任意B∈FX(A),由定义 3知c(B)是τ-闭集 .因此,c(c(B))=c(B).

定理 3 设(A,τ)是GJts,i是闭包算子 .则算子i有如下性质:

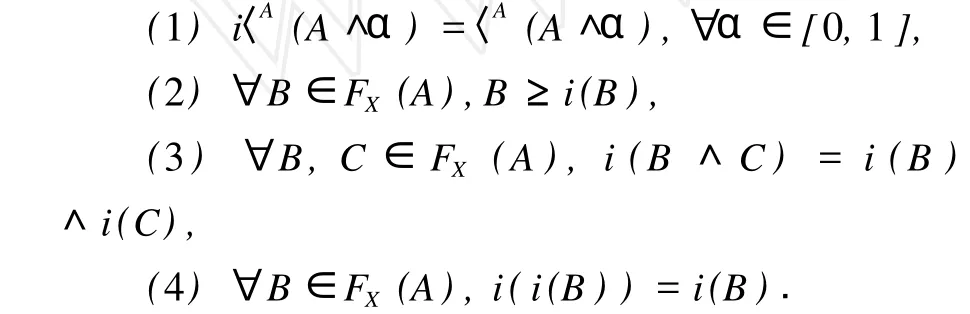
证明 定理 3的证明方法可类似定理 2,这里略去 .

由上可知,若τ是定义在A上的GJt,则可定义A上的闭包算子c和内部算子i.现在研究相反的问题,也即是说,若假设A上没有定义拓扑,有一满足定理 2的算子c:A→A,或是满足定理 3的算子i:A→A,能否由c或i定义上A的Gunther Jäger拓扑τ呢?如果能够定义τ,则可以得到拓扑空间(A,τ),从而由定义 3又可以分别定义A上的闭包算子c1和内部算子i1,那么,是否有i1=i和c1=c分别成立呢?下述定理 4和定理 5分别给出了肯定的回答 .

定理 4 设c:A→A是满足定理 2的算子,τ:={B∈FX(A);〈AB=c(〈AB)}.则 τ是A上的GJt.同时,任意B∈FX(A),设d(B):=∧{H;H⊇B,〈AH∈τ},则d(B)=c(B).

证明 首先,证明τ是A上的拓扑 .

由c(〈A〈A(A∧α))=c(A∧α)=A∧α=〈A〈A(A∧α)成立,则〈A(A∧α)∈τ.又设G,H∈τ,则c(〈AG)=〈AG,c(〈AH)=〈AH,因此,c(〈AG∧H)=c(〈AG∨〈AH)=c(〈AG)∨c(〈AH)=〈AG∨〈AH=〈AG∧H.故G∧H∈τ.最后,设Gt∈τ,

综上证得τ是A上的拓扑 .下面证明对任意B∈FX(A),d(B)=c(B).

设〈AH∈τ,B≤H,则c(B)≤c(H)=H.由d(B)的定义可知c(B)≤d(B).由定理 2(4)知,对任意B∈FX(A),有c(c(B))=c(B)成立 .即c(〈A〈Ac(B))=〈A〈Ac(B). 因此〈Ac(B)∈τ,从而由d(B)的定义知d(B)≤c(B).即证d(B)=c(B).

定理 5 设i:A→A是满足定理 3的算子,τ:={B∈FX(A);B=i(B)},则τ是A上的GJt.同时,对任意B∈FX(A),设j(B):=∨{H;H⊆B,H∈τ},则j(B)=i(B).

证明 首先,证明τ是A上的拓扑 .

由i(〈A(A∧α))=〈A(A∧α)知〈A(A∧α)∈τ.设G,H∈τ,则i(G)=G,i(H)=H,从而G∧H=i(G)∧i(H),因此,G∧H∈τ.最后,设Gt∈τ,∀t∈T,则i(Gt)=Gt.验证i(∨Gt)=Gt.易知i(∨Gt)≤Gt.故只需证i(∨Gt)≥Gt.由于任意t∈T,i(Gt)=Gt,则Gt=i(Gt)≤i(∨Gt),因此 ∨Gt≤i(∨Gt).即证i(∨Gt)=Gt.从而 ∨Gt∈τ.

综上证得τ是A上的拓扑 .下面证明对任意B∈FX(A),j(B)=i(B).

设任意H∈τ,H≤B,则H=i(H)≤i(B).由j(B)的定义知j(B)≤i(B).又由定理 3(4)及j(B)的定义,有i(B)∈τ且i(B)≤j(B).从而任意B∈FX(A),j(B)=i(B).

3 结论

本文给出了 Gunther Jäger拓扑空间中的闭包算子和内部算子的定义,研究了它们各自的性质,并证明了它们与 Gunther Jäger拓扑是可以相互确定的 .从而为更深入地研究 Gunther Jäger拓扑空间提供了理论基础 .

[1]Compactness and connectedness as absolute properties in fuzzy topological spaces,Fuzzy Sets and Systems.94(1998)405-410

[2]R.Lowen,Fuzzy topological spaces and fuzzy compactness,J:Math:Anal:Appl:56(1976)621～633.

[3]罗承忠.模糊集引论[M].北京:北京师范大学出版社,1989

[4]张文修.模糊数学基础[M].西安:西安交通大学出版社,1984

[5]王国俊.拓扑空间论[M].西安:陕西师范大学出版社 .1988

The study of the closure operator and an interior operator in topological space

HAN Yuanliang

(Depar tment ofBasic Curriculum,North China Institute of Science and Technology,Yanjiao Beijing-East 101601)

This paper firstly defines a closure operator and an interior operator in topological space respectively,and studies their properties.Secondly proves the two operators and topology can define each others.

Fuzzy sets;topological space;closure operator;interior operator

0189.13

A

1672-7169(2010)03-0068-03

2010-07-05

韩元良 (1982-),男,河南沈丘人,硕士,华北科技学院基础部教师,研究方向:格上拓扑学。