pósa-条件下的图的 Z4-连通性

张 岳,尹建华

（海南大学信息科学技术学院,海南海口 570228）

pósa-条件下的图的 Z4-连通性

张 岳,尹建华

（海南大学信息科学技术学院,海南海口 570228）

一个满足 pósa-条件且阶至少为 3的简单图G是A-连通的当且仅当G≠C4,其中A是阶至少为 4的阿贝尔群.

pósa-条件;群流;群连通性

为了给出图的群连通性定义,先给出图的一些基本概念.本文中所涉及的图均为有限图,且可以包含多重边和环.图G的顶点集和边集分别记作V（G）和E（G）.若一个图不包含多重边和环,则称之为简单图.设D是无向图G的一个定向且v?V（G）,则用E+（v）（或E-（v））表示以v为尾（或头）的边构成的集合.n阶循环群记作Zn,其中n≥2.设V1,V2是V（G）的 2个不相交的子集,e（V1,V2）表示一个顶点在V1中另一个顶点在V2中的边的个数.

令D是一个定向图,A是一个阿贝尔群（“0”为单位元的加法群）,φ:E（D）→A是一个函数,如果 0φ（E（D））,则称φ是处处不为零的.对每个顶点vV（D）,设函数 ∂φ:V（D）→A为 ∂φ（v）=∑ φ（e）-

e∈E+（v）∑e∈E-（v）φ（e）且有 ∑v∈V（D）∂φ（v）=0.如果 ∂φ的值恒等于零,则称φ为流或A-流.如果对于每个满足∑v∈V（D）p（v）=0的函数p:V（D）→A,总能找到处处不为零的函数φ:E（D）→A使得 ∂φ=p,则称D是A-连通的.

如果φ是D中的一个处处不为零的流,则对D中任意一条边e,将e的方向反向,用 -φ（e）替换φ（e）,所得到的仍然是D中的一个处处不为零的流.由此可见一个处处不为零的流的存在性并不依赖于边的定向,而只与原来的无向图有关.因此,如果无向图G的某个定向有处处不为零的A-流 （是A-连通的）,则称G有处处不为零的A-流（是A-连通的）.因此,接下来只讨论无向图的群连通性.

群连通的概念是由 Jaeger等人[2]在研究和推广流的问题过程中引入的.在文献[2]中,有如下猜想:

猜想 1[2]:任何一个 5-边连通图都是Z3-连通的.

猜想 2[2]:任何一个 3-边连通图都是Z5-连通的.

上述 2个猜想蕴含着 Tutte的著名的 3-流猜想和 5-流猜想.

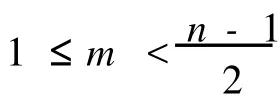
1）pósa-条件包含Ore-条件,反之不成立.

2）如果G满足 pósa-条件,则G是哈密顿图,G有一个处处不为零的 4-流,但G不一定是Z4-连通的.

令A是阶至少为4的阿贝尔群.在文献[4]中,Sun J Z等人证明了一个满足Ore-条件且阶至少为3的简单图G是A-连通的当且仅当G≠C4.在本文中将进一步证明一个满足 pósa-条件且阶至少为 3的简单图G是A-连通的当且仅当G≠C4,见定理 1.

1 主要结论

设G是一个图,X⊆E（G）.在G中将集合X中的每条边e的 2个顶点重合,然后去掉边e所得到的图称为G收缩X,记为G/X.为简单起见,把G/{e}记作G/e,把G/E（H）记作G/H.为了证明主要结论,首先给出下面几个引理.

引理 1[3]设A是一个阿贝尔群,H是G的子图.如果H和G/H都是A-连通的,则G也是A-连通的.

引理 2 设A是一个阿贝尔群.有下面几个结论

定理 1 设|G|=n≥3.如果G满足 pósa-条件,则G是A-连通的当且仅当G≠C4,其中A是阶至少为 4的阿贝尔群.

证明 如果G是A-连通的,则根据引理 2中的结论1）,G≠C4.反之,如果G≠C4,将证明G是A-连通的.当n=3时,G显然是一个三角形,根据引理 2中的结论 1）,G是A-连通的.接下来假设n≥4,根据G是否包含三角形来分 2种情况讨论.

情况 1G包含三角形.

[1]CHEN J J,ESCHEN E,LA IH J.Group connectivity of certain graphs[J].Ars Combin.,2008,89:141-158.

[2]JAEGER F,L IN IAL N,PAYAN C,et al.Group connectivity of graphs-A nonhomogeneous analogue of nowhere zero flow properties[J].J.Combin.,Theory Ser.B,1992,56:165-182.

[3]LA IH J.Group connectivity of 3-edge-connected chordal graphs[J].Graphs Combin.,2000,16:165-176.

[4]SUN J Z,XU R,Y IN J H.Group connectivityof graphs satisfyingOre-condition:proceeding 2008 InternationalConference on Foundations of Computer Science,LasVegas,July 14-17,2008[C].USA:Csrea Press,2008:21-24.

Z4-connectivity of Graphs Satisfying pósa-condition

ZHANG Yue,Y IN Jian-hua

（College of Information Science and Technology,Hainan University,Haikou 570228,China）

In this paper,a simple graphGsatisfying pósa-condition withV（G）≥3 isA-connected if and only ifG≠C4was showed,in whichAis an abelian group andC4is a cycle of length 4.

pósa-condition;group flow;group connectivity

O 157.5

A

1004-1729（2010）03-0209-03

2010-04-06

国家自然科学基金项目 （10861006）

张岳（1986-）,女,河北邢台人,海南大学信息科学技术学院应用数学 2008级硕士研究生.

尹建华 （1970-）,男,湖南祁阳人,海南大学信息科学技术学院应用数学系教授,博士.