煤矿井下OFDM自适应调制技术

王 娟, 付家才

(黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)

煤矿井下OFDM自适应调制技术

王 娟, 付家才

(黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)

煤矿井下环境恶劣,多径效应带来噪声增加和误码率上升,使通信质量下降。针对这一情况,将正交频分复用(OFDM)自适应调制技术引入井下无线通信系统,选择瑞利衰落信道模型,采用 SVD算法和低通滤波、三次样条插值算法进行信道估计和插值,并对OFDM自适应调制算法进行性能仿真。结果表明,自适应调制算法的误码率性能明显优于固定调制;SBLA自适应调制算法比 Greedy、Fishcher和 Chow算法更易实现;低通滤波插值算法比三次样条插值法更能准确估计信道特性。该研究为煤矿井下信息的实时、高速、准确传输提供了技术参考。

正交频分复用;井下无线通信;自适应调制

煤矿井下瓦斯、温度、风量等安全参数实时、准确地传输与处理,是保障煤矿井下安全生产的重要环节。目前,煤矿井下的信息传输仍以有线方式为主,存在性价比低、线路复杂、依赖性强且不易维护等缺点,尤其在出现爆炸、塌垮等危险事故时,传输系统中的硬件设备,如传感器、传输线缆等易受损,导致无法为抢险和搜救工作等提供准确信息[1]。煤矿井下通信环境空间有限、非自由,巷道壁粗糙且机电设备多,电磁波在传播过程中易发生反射或散射,以致到达接收设备的信号是来自不同传播路径的信号合成,而产生多径传播现象[2]。多径干扰信号的频率选择性衰落和路径差引起的传播时延,会使信号产生严重的失真和波形展宽,导致码间串扰,不但会引起噪声增加和误码率上升,甚至有可能使某些通信系统无法正常工作。因此,寻找适合于煤矿井下信道特性的无线调制技术是实现井下无线通信的关键。

笔者将OFDM自适应调制技术应用于井下无线通信系统。在保持传输速率恒定的前提下,根据矿井传输信道的具体特点,选择适合各载波的调制方案,可实现井下信息的高速和准确传输。

1 调制模型

煤矿井下OFDM自适应调制模型如图 1所示。由图 1可见,该模型主要由信道估计、自适应比特和功率的分配与提取、调制与解调、IFFT与 FFT变换等单元组成。其工作原理为:由动态的自适应比特和功率算法对并行的二进制并行信息比特流进行比特和功率的分配,在每个 OFDM周期内,由调制器得到频域符号,经过 IFFT和插入循环前缀后,得到时域信号。这些时域信号经频率选择性衰落的井下信道送到接收端,在接收端去除循环前缀后经过FFT得到频域信号,再由解调器和比特分配信息提取出二进制比特流。

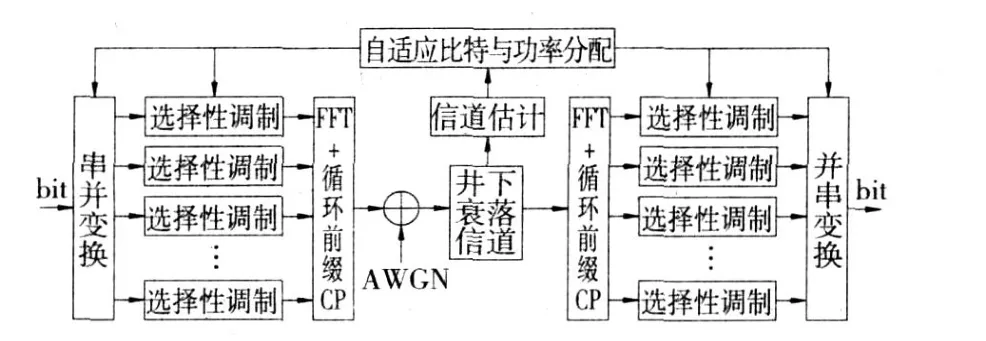
图1 井下OFDM自适应调制模型Fig.1 M odel of underground adaptive OFDM

2 信道模型选择与估计

不同的信道模型对仿真结果有直接影响,为使OFDM自适应调制模型更接近煤矿井下的实际工况,需依据井下信道的传输特性,建立正确的井下信道模型。常见的无线通信系统中,由发射机发出的射频信号在传播过程中经常受到各种障碍物和其他移动物体的影响,导致接收端收到的信号是来自不同传播路径的信号叠加。瑞利分布是用于描述平坦衰落或者独立多径分量情况下接收信号包络统计特性的一种典型分布。如果发射机和接收机之间的多径传播中存在一个主要的静态信号分量,还存在视距传播路径,接收信号的包络则服从莱斯分布[3]。与地面的无线信道相比,煤矿井下多径传播现象严重,因而从发射机到接收机基本不存在直射信号,信号幅度会产生严重的随机性衰落。显然,经井下无线信道传输后到达接收端的信号包络服从瑞利分布,故文中首选瑞利衰落信道作为煤矿井下的信道模型。

煤矿井下的信道具有多径衰落和时变特性,为获得实时的信道特性,必须对所建立的瑞利信道模型进行准确、动态的信道估计。信道估计应用基于导频的信道估计算法,具体分为两步:一是在接收端对导频信号特性进行估计,一般采用奇异值分解(SVD)算法;二是在得到导频估计信息后进行插值算法处理,得到所有传输数据信息的子载波的信道特性[4]。在常用的插值算法中,线性内插算法比较简单但估计误差大,而低通滤波和三次样条插值算法一般具有较高的估计精度,因此,文中选用后两者。

3 调制算法

比特与功率分配算法是煤矿井下实现OFDM自适应调制的关键,其基本思想是根据所检测到子载波的瞬时性能,确定各子载波采用何种调制方式,以达到在满足一定传输性能要求的前提下,使系统总的发射功率最低。较经典的自适应调制算法有注水算法、Greedy算法、Chow算法以及 Fischer算法等[5],但这些算法较为复杂,作为比特加载算法计算量大,很难保证时变信道下传输数据的实时性。

简单分组比特分配算法(SBLA)简化了比特分配算法,将子载波成组的捆绑在一起,根据每组子载波的平均信噪比来确定采用何种调制方式。这种算法计算复杂度降低,主要缘于预先确定了采用不同调制方案所需的信噪比阀值。信噪比阀值的绝对值是可变的,但各个阀值之间的间隔是不变的,就像一个标尺上面排列着等距的数值一样。这个“标尺”的绝对位置由全部子载波的平均信噪比决定,“标尺”上各个阀值的间隔是由高斯白噪声信道下,各种调制方式的误比特率(BER)曲线在同一处的值得到的。将所有子载波分成 7组,且选定BER曲线为 10-3处,则信噪比(SNR)阀值间隔如图2所示。

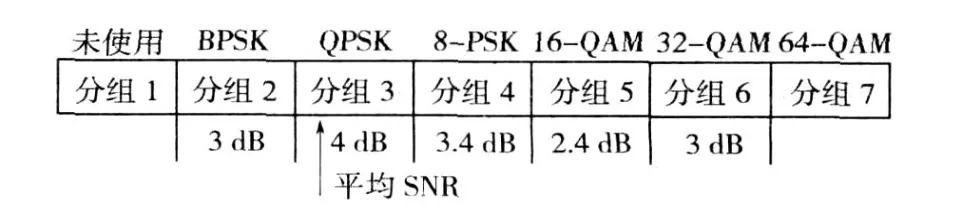
图2 信噪比阀值间隔Fig.2 Threshold interval of signal to noise ratio

SBLA算法的具体处理步骤为:

(1)求解信噪比。将OFDM信号的子载波分成N个子带,计算各组子载波的信噪比γi,i=1,2,…, N。由于每个子载波的噪声能量独立于信道的传递函数,故第i个子载波的信噪比γi可表示为

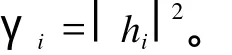
(2)设置信噪比阀值。计算每一区间段信噪比的平均值,并记为γstd。由各种调制方式在高斯白噪声信道下的BER曲线可得γstd=[0 3 6.5 10.2 13.1 15.8 18.8],其提供了7种可供选择的调制方式,分别是不使用、BPSK、QPSK、8-PSK、16-QAM、32-QAM、64-QAM。全部子载波的平均信噪比γmean为

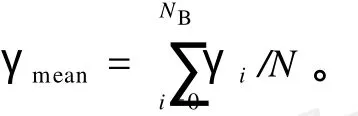
(3)设置目标调制深度Rtarget。假设系统采用固定调制,且调制方式为 QPSK,则Rtarget=2。根据γmean和Rtarget,可得平移后的平均信噪比阀值γ′std:

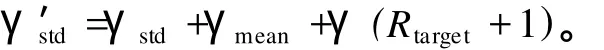
可见,“标尺”上的目标调制方式的位置恰好与平均信噪比重合,如图 2所示。

(4)确定调制方式。根据信噪比阀值和各组γi,从备选的 7种调制方式中确定相应的调制方式,可得

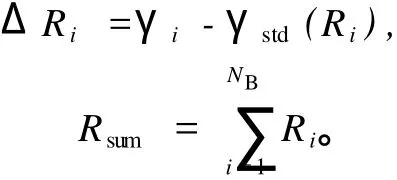
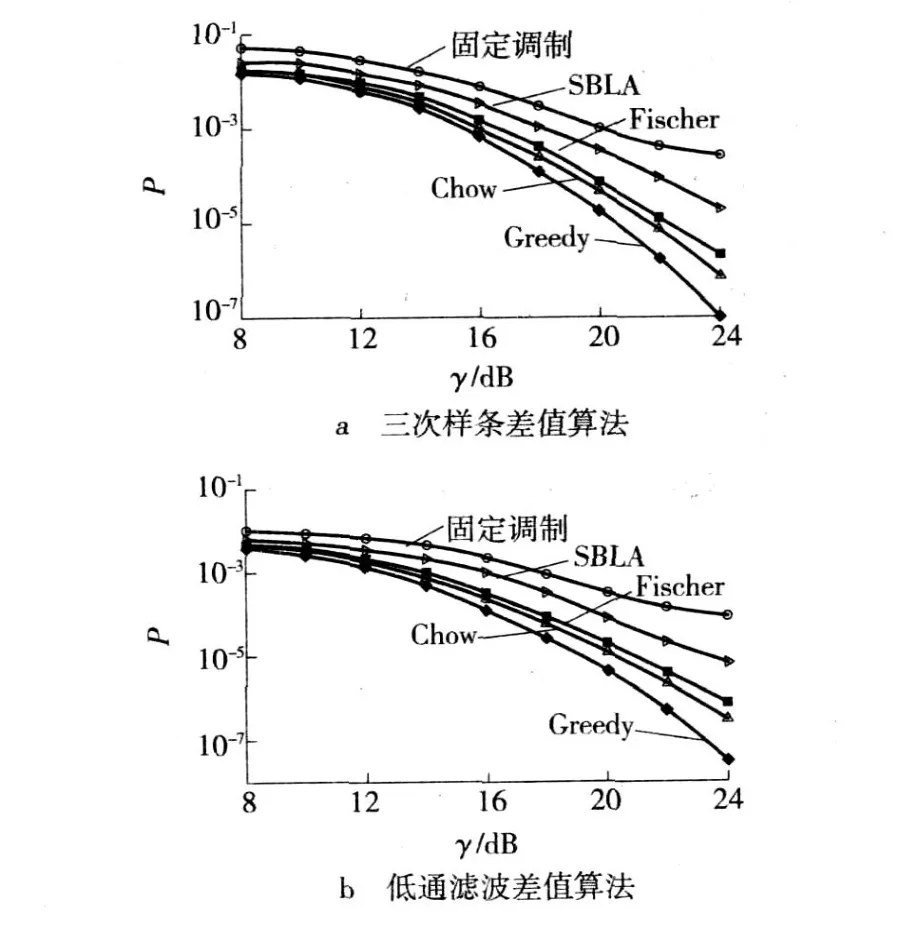
(5)调整Ri。设等待分配的比特总数为RT,若Rsum=RT,则转到步骤 (6);否则调整Ri。调整方法为:若Rsum>RT,应找到最小的ΔRi,且Ri>0,调整R′i=Ri-1,R′sum=Rsum-1,ΔR′i=ΔRi+1;若Rsum

(6)处理信号功率。应用子载波归一化方法,给所有已使用子载波的信号乘以一个比例因子,使得总的信号功率等于设定的信号功率。

4 仿真与性能分析

应用MATLAB软件对基于瑞利信道模型的OFDM自适应调制算法进行性能仿真,其中 SBLA算法参照图 2中的阀值间隔对各子载波进行分组,并提供 5种调制方式,分别为固定调制、BPSK、QPSK、16-QAM、64-QAM,对应的比特分配数目集B={0,1,2,4,6}。另外,设OFDM固定调制系统中各子载波均采用 QPSK调制方式,得到的误码率(P)性能曲线如图 3所示。

图 3 固定调制和自适应调制的性能曲线Fig.3 Performance curves of fixed modulation and adaptive modulation

由图3可知,在煤矿井下传输模型中,自适应调制比固定调制具有更优越的抗噪声性能,且这种优越性随信噪比的提高而愈加明显。在误码率相同的条件下,使用自适应调制所需的发射功率比固定调制低。与 Greedy、Fischer和 Chow算法相比,S BLA在进行比特的初始分配时只需估计出各个子带的γmean,然后根据预先确定的 S NR门限选定相应的调制级别,即完成初始化比特分配,降低了计算复杂度。因此,在煤矿井下OFDM自适应算法的应用中,S BLA算法减少了系统的信令开销和运算量,在信噪比较高的子信道传输较多的比特,在信噪比较低的子信道传输较少的比特,从而使得绝大多数发射信号的功率集中在信道衰减较小的频带范围内,可极大提高OFDM系统的吞吐量。

图4 不同差值算法的性能曲线Fig.4 Performance curves of different algorithm

为了描述不同插值算法对信道估计误差的影响,文中分别给出了三次样条插值算法和低通滤波插值算法时固定调制及自适应调制的性能曲线,如图4所示。经过比较,在信噪比相同的条件下,采用低通滤波插值算法时系统的误比特率更低;在误比特率相同的条件下,低通滤波插值算法比三次样条插值算法的信噪比更低。所以,采用低通滤波插值算法能够更准确的估计信道特性、减小误差、提高系统性能。

5 结束语

煤矿井下 OFDM自适应调制系统以井下无线通信信道模型为基础,由 SVD信道估计算法和低通滤波插值算法及 SBLA自适应比特和功率分配算法构建而成。该系统既可以解决煤矿井下多径干扰严重的问题,又可以提高井下通信的抗噪性和实时性,使矿井安全参数等数据在井下稳定可靠地传输,保证了通信质量,有利于煤矿安全生产。

[1] 杨 维,程时听,孙继平.矿井无线通信与频率资源利用[J].煤炭学报,2001,26(5):535-538.

[2] 王文博,郑 侃.宽带无线通信OFDM技术[M].北京:人民邮电出版社,2007.

[3] 李 子,蔡跃明.Rayleigh衰落信道的仿真模型[J].解放军理工大学学报:自然科学版,2004,5(2):1-8.

[4] 裴红霞,徐 钊,张晓光.OFDM自适应算法在煤矿井下的应用研究[J].现代电子技术,2009,9(1):43-46.

[5] 陈浩氓,徐巧勇,王宗欣.一种新的OFDM系统自适应调制算法[J].复旦学报:自然科学版,2005,(1):75-79.

OFDM adaptive techniques in coalm ine

WANG Juan,FU Jiacai
(College of Electric&Infor mation Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China)

The response to the communication quality degradation resulting from increasing noise and bit error rate due to the hostile communication environment of coal mine and occurrence of multi-path effect in underground mines leads to the use of OFDM of adaptive modulation to underground wireless communication systems,as dictated by featuresof the coalminewireless communication,selection of rayleigh fading channelmodel,and use of SVD algorithm,low-pass filter interpolation algorithm and cubic spline interpolation algorithm for channel estimation and simulation of the system perfo rmance.The results show thatBER of adaptive modulation algorithm is superior to the fixed modulation;SBLA adaptive modulation algorithm is easier to achieve than the Greedy,Fishcher and Chow algorithm;Low-pass filter interpolation algorithm givesmore accurate estimation of channel characteristics than Cubic spline interpolation.The study provides a technical reference for real-time,high-speed and accurate transmission of information in underground coalmine.

OFDM;underground wireless communication;adaptive modulation

TN914

A

1671-0118(2010)02-0135-03

2010-03-02

王 娟(1981-),女,黑龙江省佳木斯人,讲师,硕士,研究方向:信息传输与处理,E-mail:mermaid_wj@sina.com。

(编辑荀海鑫)