一种唯相波束赋形的快速方法
2010-12-15杜海龙闫鲁滨
杜海龙,闫鲁滨
(中国空间技术研究院总体部,北京 100094)
0 引 言
在星载天线中,赋形波束天线有着广泛的应用。例如用于固定卫星服务的星载通信天线要求具有覆盖服务区域的赋形波束,以提高服务区域内的增益,减小对服务区域外的干扰;遥感卫星的星载数传天线需要具有地球匹配波束,以弥补星地间传输途径的空衰变化;星载SAR为了满足成像幅宽的要求,需要宽波束天线;低轨移动通信系统(铱星系统、全球星系统)的赋形多波束天线等。相控阵天线波束赋形灵活、快捷,因此在星载天线中有极大的发展潜力。
天线波束赋形的方法可以划分为两类:第一类是单元的激励幅度和相位同时调整,即幅度、相位同时加权;第二类是只调整单元的激励相位,即相位加权。幅度、相位加权会得到更好的赋形结果,但幅度加权要求增加幅度控制的硬件设备,增加了系统的复杂程度。而仅相位加权只利用相控阵的移相器,不需要另外增加硬件设备,因此具有很好的工程应用价值。
相控阵天线的唯相加权波束赋形是一个非线性的优化问题,可以采用各种优化算法来完成。常规的方法是以单元的激励相位作为优化变量,通过优化算法来完成,如Davis将最小二乘法应用于唯相加权的阵列波束赋形[1];Haupt用遗传算法实现唯相加权的自适应零点生成[2];Khzmalyan采用单坐标最小化的方法实现唯相加权波束赋形和自适应零点生成[3]。常规的方法当单元的数量较多时,优化变量也就很多,这样导致优化过程非常耗时,优化的结果也不是很理想。文献[4]中提出了一种用于唯相加权波束赋形的级数展开方法,这种方法通过把单元的激励相位用一组系数待定的基函数展开,使得优化变量由单元的激励相位转化为级数中的待定系数。这样就可以极大地减少优化变量的数量,使得优化过程能够快速完成并且能够收敛到理想的结果。文献[4]中给出了一维线阵的处理方法,但在实际应用中,多数是处理平面阵的问题。本文发展了一维阵的方法,给出了二维平面阵的处理方法,通过对波束展宽赋形的数值仿真,结合线阵和平面阵验证了这种方法的有效性。文中还通过一个48个单元的相控阵的实验测试验证了用这种方法得到的结果的正确性。
1 唯相加权波束赋形的级数展开法
唯相加权波束赋形的核心问题是寻找一组最优的激励相位分布使阵列的辐射方向图逼近指定的方向图。对于最优的相位分布可以通过一组基函数来展开,这样最优相位分布对应一组固定的展开系数。因此唯相加权波束赋形可以转化为寻找一组最优的展开系数的问题,通过这组展开系数来确定阵列的激励相位分布。当阵列的单元数量较多时,展开系数的个数要远少于单元的数量,因此通过级数展开的方法可以减少波束赋形时优化变量的数量,使得算法能快速收敛。具体讨论如下。
1.1 线阵唯相加权波束赋形的级数展开法
对于一个等幅激励的N元直线阵,其远场方向图为
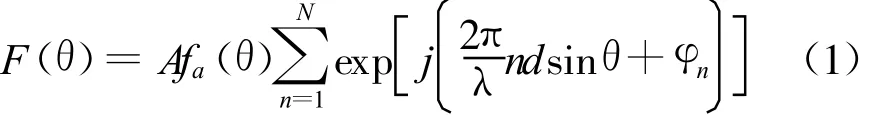
式中 fa(θ)为单元方向图,φn为单元的激励相位,d为单元间距,λ为波长,A为激励幅度,θ为阵轴法向与观察方向的夹角。常规的波束赋形方法是以φn为优化变量进行优化赋形的。因此优化变量的个数就是阵列中单元的数量N。
在级数展开法中,单元的激励相位用一组基函数展开,如下式
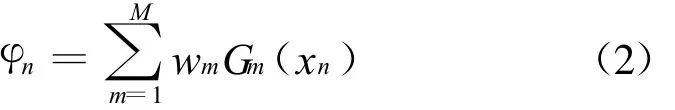
式中wm为待定系数;Gm(x)为第m个基函数,可以取三角函数、切比雪夫函数等;xn为第n个单元在阵列中的相对位置,可以通过下式确定
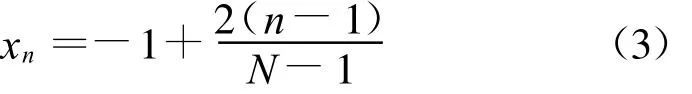
通过(2)式的变换,单元的激励相位仅与级数中的待定系数wm有关,因此波束赋形时,优化变量就由φn变为wm。优化变量的个数就由N变为M 。对于大型阵列M是远远小于N的,因此这种级数展开的方法可以起到减少优化变量数量的目的,通过减少优化变量的个数,使得波束赋形能够快速完成。
1.2 平面阵唯相加权波束赋形的级数展开法
以矩形栅格排列的等幅激励的平面阵为例,其远场方向图为
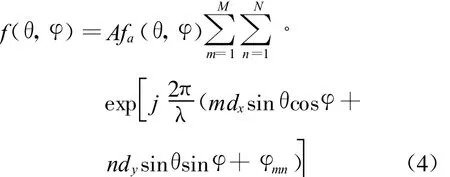
式中 fa(θ,φ)为单元方向图,φmn为单元的激励相位,d x、dy分别为 x方向和y方向的单元间距,λ为波长,A为激励幅度,(θ,φ)为观察方向在球坐标系下的分量。单元的激励相位用级数展开,可以表示为
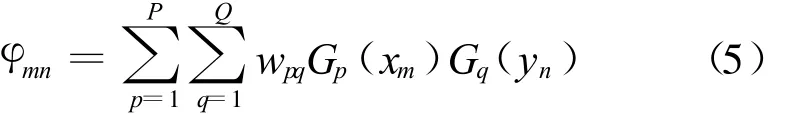
式中wpq为待定系数;Gm(x)、Gn(y)为关于 x、y的基函数,同样可以取三角函数、切比雪夫函数等;xm、yn为第(m,n)个单元在阵列中的相对位置,可以通过下式确定
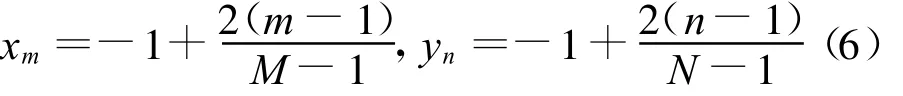
通过(5)式的变换,优化变量由φmn转化为wpq,和线阵类似可以起到减少优化变量的目的。
2 仿真分析及实验验证
下面以线阵和平面阵的波束展宽赋形为例,分别采用常规的以单元激励相位为优化变量的方法和级数展开法进行仿真分析。
波束展宽要求在展宽区满足给定的增益起伏,在副瓣区要求小于给定的副瓣电平,同时还应使展宽区内增益尽可能高,因此采用了下面的适应度函数[5]

式(7)中首先对阵列增益进行采样,i为采样点,fi为第i点的阵列增益。波束展宽区内采样2S+1点,(7)式中第一式对应展宽区的平均阵列增益,第二式对应最高副瓣电平,第三式对应展宽区内最大的增益起伏,第四式中w1和w2为调节参数。这样由(7)式确定的适应度函数就兼顾到了主瓣增益、主瓣区的起伏电平和副瓣电平,因此可以得到很好的优化效果。
2.1 线阵的波束展宽仿真
以64元的均匀直线阵为例,单元间距d=λ/2,各单元激励幅度为1。要求波束展宽后的波束宽度BW0=8°,最大起伏电平±0.5 dB,相对最大副瓣电平SLL0=-10 dB,采用唯相加权赋形,假定相位对称。这里采用遗传算法进行优化赋形。遗传算法是一种模拟自然界生物进化的随机搜索算法,遗传算法按照优胜劣汰的原理从上一代种群中选择优秀的个体,然后利用交叉、变异操作产生新的个体,逐代演化来逼近最优解。遗传算法是一种全局优化算法,而且对适应度函数也没有特殊要求,非常适合解决唯相加权波束赋形这类复杂的非线性优化问题。
图1为采用常规方法赋形的结果,这时优化变量有32个。图2为采用级数展开法的赋形结果,级数展开采用了切比雪夫多项式,根据(2)式,单元的激励相位为
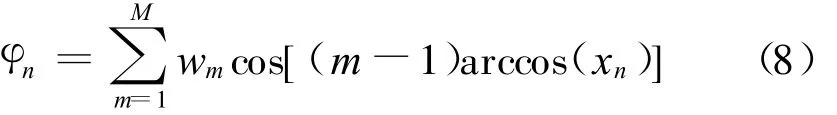
上式中取前6项基函数,因此优化变量有6个。
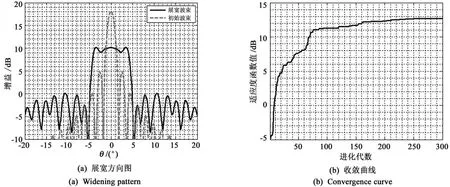
图1 采用常规方法的线阵波束展宽赋形Fig.1 Beam widening of linear array by conventional method
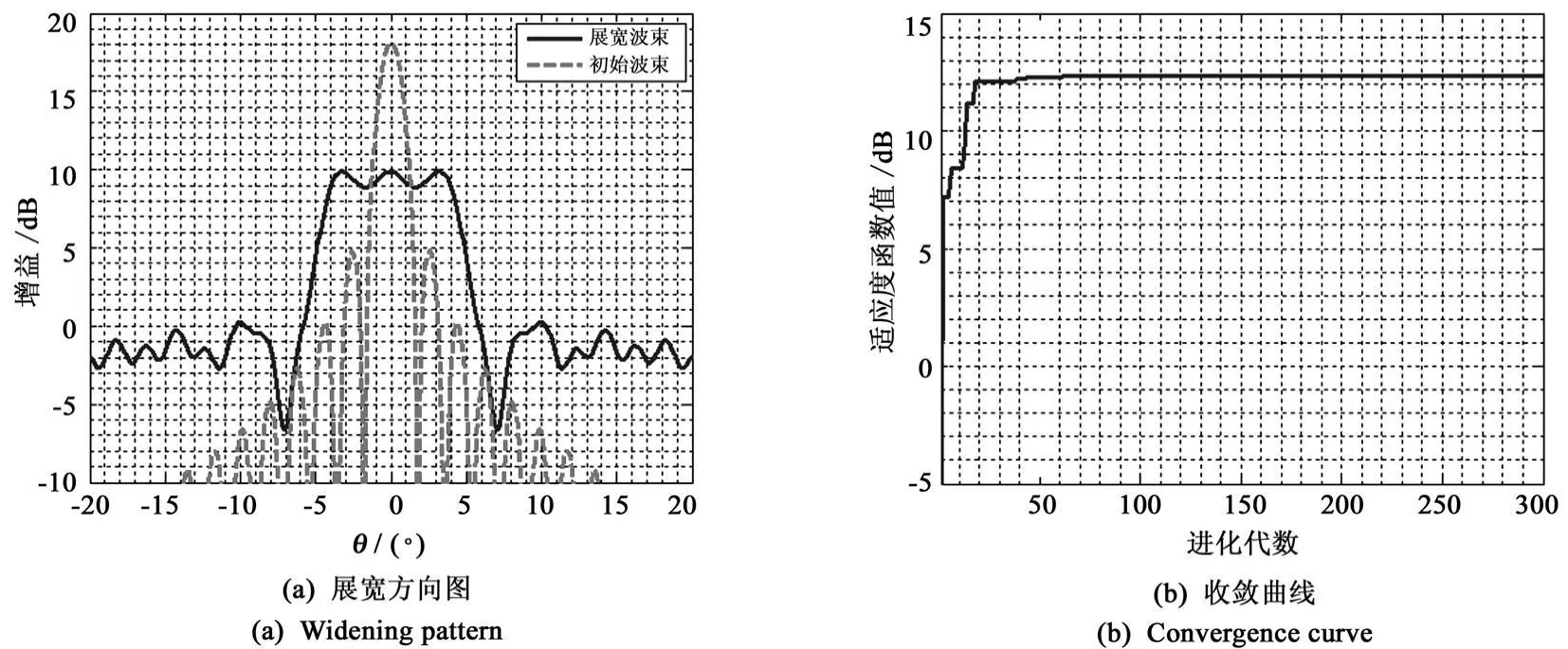
图2 采用级数展开法的线阵波束展宽赋形Fig.2 Beam widening of linear array by series expansion method
两种方法采用的是同样的适应度函数和同样的优化算法,因此两种方法的运算量是相同的。算法的运算速度取决于计算机的性能,因此两种方法的优劣只能通过其收敛曲线判别。图1(b)和图2(b)分别为一维线阵常规方法和级数展开法的收敛曲线。通过图1(b)和2(b)的比较,在收敛到同样的适应度函数值时,常规方法需要进化近240代,而级数展开法仅需60代,这表明级数展开法的收敛速度要明显快于常规方法。常规方法的赋形结果与级数展开法的结果相近,这可以通过图1(a)和图2(a)的比较得出。
2.2 平面阵的波束展宽仿真
以一16×16的矩形栅格排列的平面阵为例,单元间距d x=d y=λ,单元激励幅度为1,要求综合出俯仰和方位面内宽度为10°的平顶方向图,最大起伏电平±1 dB,相对最大副瓣电平SLL0=-10 dB,采用仅相位加权赋形,相位对称分布。
图3为采用常规方法赋形的结果,这时优化变量有64个。图4为采用级数展开法的赋形结果,级数展开采用了切比雪夫多项式,根据(5)式,单元的激励相位为
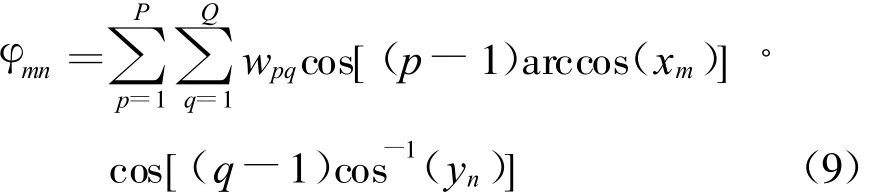
上式中取P=5,Q=5,共25个优化变量。从图3(b)和图4(b)的比较可以看出在收敛到相同的适应度函数值时,常规方法进化了近400代而级数展开法仅需50代,这表明级数展开法的收敛速度远快于常规方法。从图3(a)和图4(a)的比较可以看出由于常规方法的优化变量太多,在迭代500次后,常规方法得到的增益要比级数展开法低1.5 dB。由此可见本文所提出的方法在波束赋形应用中的优越性。

图3 采用常规方法的平面阵波束展宽赋形Fig.3 Beam widening of planar array by conventional method
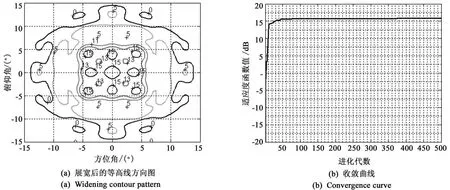
图4 采用级数展开法的平面阵波束展宽赋形Fig.4 Beam widening of planar array by series expansion method
3 级数展开法波束展宽赋形的实验验证
为了验证级数展开法得到的结果的有效性,以图5所示的现有相控阵进行了实验验证。实验相控阵为两行48个单元的多模喇叭阵列,喇叭尺寸为宽边三个波长,窄边一个波长。由于试验相控阵的限制,仅进行了E面方向图展宽赋形,展宽波束宽度设计为10°。图6中给出了测试结果与计算结果的比较,从图中可以看出测试结果和计算结果吻合的很好,主瓣区内的差异主要是由于实验相控阵各通道间的幅相误差造成的。
4 结 论

图5 实验相控阵Fig.5 Experimental phased array
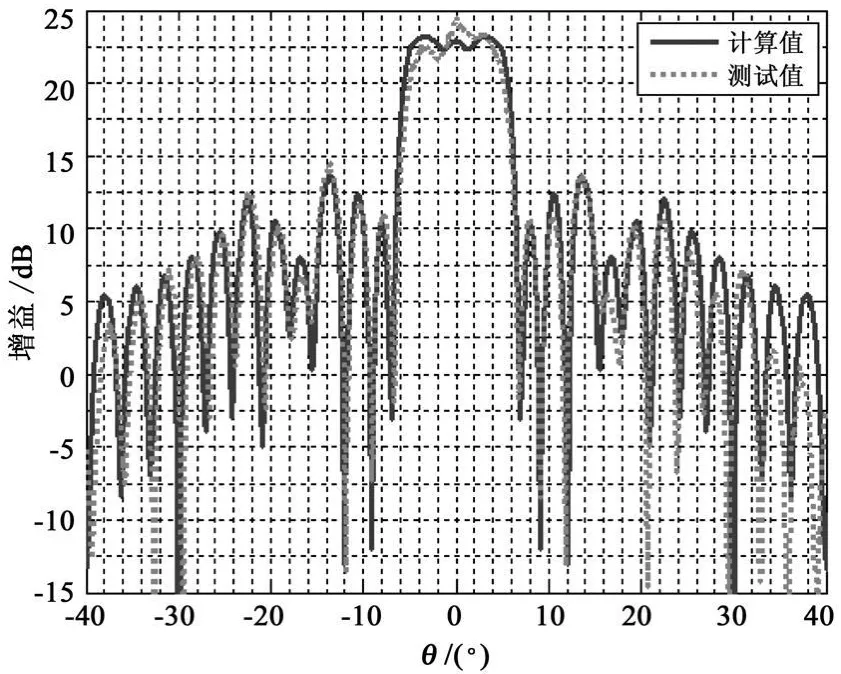
图6 实验相控阵展宽波束方向图Fig.6 Widening pattern of experimental phased array
本文发展了线阵唯相加权波束赋形级数展开的方法,给出了二维平面阵的唯相加权波束赋形的级数展开法。级数展开法通过减少波束赋形时优化变量的数量使得波束赋形能够快速完成。通过对线阵和平面阵的波束展宽赋形的仿真分析,表明级数展开法的收敛速度明显快于常规的方法。设计进行的48元相控阵的实验进一步验证了由级数展开法得到的结果的正确性。
[1] Davis R M.Least mean square phase-only adaptive algorithms[J].IEEE Antennas and Propagation International Symposium,1996,34:1184-1187.
[2] Haupt R L.Phase-only adaptive nulling with genetic algorithms[J].IEEE Transactions on Antenna and Propagation,1997,45(2):1009-1015.
[3] Khzmalyan A D.The phase-only shaping and adaptive nulling of an amplitude pattern[J].IEEETransactionson Antenna and Propagation,2003,51(2):264-272.
[4] Gatti R V,Marcaccioli L,Sorrentino R.A novel phase-only method for shaped beam synthesis and adaptive nulling[C].33rd European Microwave Conference,Munich 2003:739-742.
[5] Haupt RL,Johnson JM.Dynamic phase-only array beam control using a genetic algorithm[C].Proceedings of the First NASA/DOD Workshop,Pasadena,USA,1999:217-224.
