Generation and Propagation of Nonlinear Surface Waves in a Fully-Nonlinear Wave Flume

ZHAO Xi-zeng,SUN Zhao-chen,LIANG Shu-xiu

(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)

1 Introduction

Investigation on the generation and propagation of water waves is essential for studying the interactions of such waves with marine structures.In the linear system,water waves do not change their form and keep their form permanent,as predicted by the linear solution.While the generation and propagation of nonlinear water waves are very complex phenomenon.Under resonant conditions,it is well known that a weakly nonlinear,uniform,deep water wave train suffers an instability known as Benjamin-Feir instability(Benjamin and Feir[1]),which appears in the form of growing modulations.Unfortunately,the nonlinear wave-wave interactions can affect wavefield evolution and cause significant energy transform among wavetrains in a nonresonant wavefield.The understanding of the physics of the generation and propagation of nonlinear water waves is of fundamental importance in the modeling of a sea state.

The wave generation and propagation in a wave flume has been a topic of great interest over the past few decades ever since the linear wavemaker theory was derived by Havelock[2].Experimental verifications of the linear wavemaker theory have shown that the linear wavemaker theory does not provide a wave of permanent form(Goda and Kikuya[3];Multer and Galvin[4];I-wagaki and Sakai[5];and others).The resulting waves are composed of a primary and one or more secondary waves,which comprise both the free and bound waves.The secondary free wave has a lower period than the primary wave and propagates at a slower speed.This will disturb the wave profiles and the corresponding wave spectrum.To eliminate this disturbance,Madsen[6]developed the second-order wavemaker theory in Eulerian coordinates and obtained a solution with a permanent form for weakly nonlinear long waves generated by a sinusoidally moving piston wavemaker.However,the derived solution can be applied only for an Ursell number up to about 8π2/3.Suliz[7-8]derived a semi-analytical second-order wavemaker model to predict the generation and transform of nonlinear waves in a periodic unbounded domain and a non-periodic bounded domain respectively.Our goal is to model the generation and propagation of nonlinear water waves in a fully-nonlinear wave flume.

Owing to the remarkable progress in computing facilities as well as in techniques of computational hydrodynamics,a numerical wave flume has become one of the essential tools for modeling fully nonlinear surface waves.An alternative numerical approach to solve inviscid free surface problem is to use spectral methods.It has been firstly proposed by Fenton and Rienecker[9]using the Fourier-series expansion.For free wave problem,Dommermuth&Yue[10]and West et al[11]have further improved independently the method by solving the resulting boundary value problems based on Fast Fourier Transform(FFT).Zhao and Sun[12]presented an enhanced spectral model by paying specific cares to time integrator and error considerations and have carried out the study of freak wave models(Zhao et al[13]).However,its application to fully-nonlinear simulation of gravity wave evolution was limited up to now to periodic unbounded domains.To overcome the apparent disadvantages of spectral method,one can choose a periodic domain with absorption on all the lateral boundaries(Clamond et al[14])or extend the computational domain until boundary effects essentially disappeared.This involves employing a much larger computational domain.Agnon and Bingham[15]developed a useful technique to decompose the potential into two,the additional part satisfying the non-homogeneous condition on the wavemaker,and a periodic potential which ensures the spectral expansion on the wavetank nature modes.As an original extension to Agnon and Bingham,several enhanced models are proposed(Touzé[16-17];Bonnefoy[18-19].Bonnefoy proposed a fully-spectral wave model,but with boundary conditions on the free surface and on the wavemaker being modeled up to second order with respect to the wave steepness and to the wavemaker excursion respectively.Here,a pair of fully-nonlinear formulations is presented and solved quickly and accurately by spectral methods for the free surface problem and the additional problem.

In the present work,a fully-nonlinear wave flume is derived to predict the propagation and propagation of transient nonlinear water waves.Using the concept of an additional potential proposed by Agnon and Bingham,a fully-spectral wave model is presented,where the potential is splited into two complementary parts,one additional part accounting for the wavemaker condition,and the remaining fixed part formulated in the basin without wavemaker and with adequately modified free-surface conditions.The wavemaker is located on the wall at x=0,with a starting ramp applied in order to reduce the effect of transient disturbances.To dissipate the incident wave energy,the wavetank is equipped with absorption boundary conditions located close to the wall opposite to the wavemaker.Based on the non-periodic spectral approach,investigations are carried out for the generation,propagation and transform of transient nonlinear waves with different wave steepness and wavelength.The main attention is paid to the wave profile,the wave energy spectrum,and the changes of wave profile and energy spectrum.The numerical results are compared with the linear wave solution and the predicted solution presented by Madsen.Finally,experiments observations are conducted in a wave flume and calculations are compared with experimental data.It is found that there is a fairly good agreement between the numerical and experimental data.

2 Governing equation and boundary conditions

A Cartesian coordinate system is defined with the origin located at the mean water level z=0,with x the horizontal plane and z the upward axis,as shown in Fig.1.The notion x stands for the(x,y)vector.Irrotational motion of an inviscid and incompressible fluid initially at rest is considered;surface tension is neglected.The threedimensional domain D is bounded by a free surface z=η（x,t）and by a bottom z=-h（x）,with a width Lyand length Lx.Here t is the time.The fluid motion can therefore be described by a velocity potential φ（x,z,t）satisfying the Laplace equation:

with the following boundary conditions:

Fig.1 Sketch of the wave flume

where▽=（∂/∂x,∂/∂y）,z=η denotes the free surface,which is assumed to be continuous and single-valued,the subscript t denotes the partial differentiation with respect to t,φzis the vertical gradient of the velocity potential φ,g is the acceleration due to gravity.

Using the concept of an additional potential proposed by Agnon and Bingham(1999),we decompose the velocity potential φ of the whole problem into a traditional velocity potential φtankand an additional velocity potential φwn

where φtankis the spectral potential in the fixed-geometry tank with its free surface,and φwnis an additional potential accounting for the wavemaker but not the free surface.Therefore,φtanksatisfies the equations(1.1),(1.2)&(1.3),and homogeneous Neumann conditions on the tank walls and bottom;and φwnsatisfies the equations(1.1)&(1.4),and homogeneous Neumann conditions on the tank right wall and bottom.

Substituting equation(2)into Eqs.(1.2),(1.3),the fully-nonlinear free surface boundary conditions on the free-surface z=η（x,t）can be now written as follows,by means of the Zakharov[20]surface potential φs（x,t）=φ ［ x,η（x,t）］.

Given the initial elevation η（x,t）and the surface potential φ（x,t）,the unsteady evolution of Eqs.(3.1)and(3.2)may be followed by the high-order spectral method(Dommermuth,1987;West,1987;Zhao and Sun,2008).Nonetheless,the use of spectral expansion is limited up to now to periodic unbounded domains on the free surface.To overcome this difficulty,it is necessary to seek an effective solution to Eqs.(3.1)and(3.2).

3 Numerical method

To preserve the attractive features of spectral techniques,both the velocity potential φtankand the additional potential φwmare solved by methods of spectral expansions.

3.1 Additional potential resolution φwm

Following Bonnefoy[2006],the additional potential resolution φwmin an extended basin may be sought as

where P and Q are the number of Fourier modes in the y-and z-directions,respectively,and

3.2 High-order spectral resolution φtank

In the bounded domain D where the potential φtanksatisfies the Laplace equation,in addition to these boundary conditions and bottom boundary conditions,etc.,the velocity potential φtankcan be expressed in a spectral expansion form here,knp=（kp,kn）is the wavenumber vector,with components kp=pπ/Lyin y-direction and kn=nπ/Lxin x-direction,respectively.

3.3 Implement

In the present model,the linear wavemaker boundary condition(1.4)and the second order wavemaker theory(Madsen,1971)are adopted.It enables us to solve the wavemaker boundary value problem straightforward rather than in a second order model being solved from the first order to the second order.

Firstly,the modal amplitude Apq（t）of the additional velocity φwmmay be obtained from the boundary condition Eq.(1.4)at the wavemaker for a specific target wave.Then,the free surface elevation η and the velocity φ are discretized in time for the fixed-tank boundary value problem.The knowledge of the unknowns can be updated at t+Δt through a time-marching scheme.Replaying above procedures and stopping until the set time.For our present computations,we use a fifth-order Adams-Bashford-Moulton predictor-corrector adjustment integration scheme(Zhao and Sun,2008).

3.4 Wave generation

The wavemaker is located on the wall at x=0,with a starting ramp applied in order to reduce the effect of transient disturbances.Similar to the case of physical applications of the wave generation theory,a second wavemaker theory is introduced to yield the motion of a piston-type wave generator(Madsen,1971).

with

where ω is the wave frequency of the target wave;and χ denotes the stroke of wave paddle.The generated waves are second-order Stokes waves with a permanent form and will be expressed as

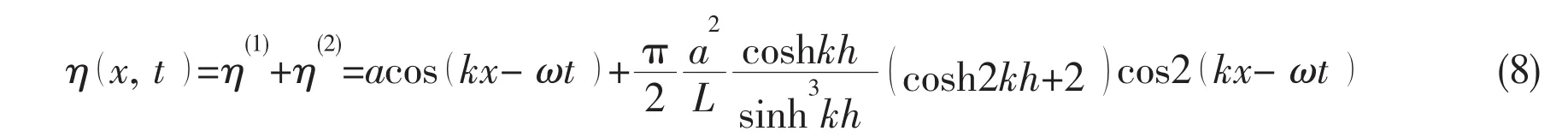
Application of the above approximate wavemaker theory was limited to waves corresponding to the criterion Ur=（2a）λ2/h3＜8π2/3.

To decrease the computational domain,a damping layer is applied close to the wall opposite to the wavemaker(Larsen and Dancy[21]).

4 Numerical results

The present wave tank is applied to investigate the generation and propagation of nonlinear water waves of different wave length λ and wave steepness ε＝ka(k standing for wave number and a for wave amplitude).The results are analyzed with the emphases on the effect of wave length and wave steepness on the propagation and transformation of a wave train.The main attention is paid to the wave profile,the amplitude spectrum,and the changes of wave profile and amplitude spectrum due to the interactions of wave components in the wave train.The wave spectrum can be obtained by applying a Fourier analysis.Our results are compared to the linear wave solution and the predicted solution from Eq.(8)as presented by Madsen(1971).

Case studies are presented in two dimensions and a constant water depth of h=0.4m.Several cases are conducted with ratios of the wavelength(λ)to the water depth(h)as λ/h=4,6,8.Moreover,a range of input wave steepness is considered from 0.05 to 0.25.The free surface elevation is measured at x=10.0m.Tab.1 lists the values of Ursell number(Ur)simulated here.

Based on the above numerical model,we first consider the evolution of waves with low steepness ε=0.05.The application of the present approach to waves of low steepness enables us to verify the accuracy of the present numerical scheme because the outcome of the model should be basically the same as the linear solution.The wave profiles and the amplitude wave spectrums are presented in Fig.2 and are compared with the linear solutions.Fig.2(a)shows the wave profiles,while Fig.2(b)presents the amplitude wave spectrums.With the small steepness,there is a good agreement between the numerical result and the linear solution.

Tab.1 Numerical conditions

Fig.2(a) Free surface elevation of ε=0.05 at x=10m:——simulation,……linear solution;(b)Amplitude of Fourier series corresponding to waves of ε=0.05 at x=10m:——simulation,……linear solution

For the case of the small steepness,ε=0.05,the nonlinear wave effects and effects associated with the interaction of water waves in a wave train are negligible or are of secondary importance.The propagation of waves of the small steepness can be predicted by linear wave theory in a wave flume.Fig.3 and Fig.4 concern the surface elevations resulting from the larger steepness(ε=0.1,0.2)for three ratios of the wavelength to the water depth λ/h=4,6,8.In each figure,the free surface elevation measured at x=10.0m is compared with the linear wave solution and the corresponding amplitude wave spectrum.The increased values of the Ursell number produce divergences from the linear solution in these figures.Moreover,the discrepancies between the outcome of the numerical simulations and the first-order theoretical solutions are increasing with increasing wavelength and steepness.The wave crests become higher,while the adjacent wave troughs become less deep.The nonlinearity therefore creates a steeper wave envelope.This is consistent with a local increase in the energy density due to a transfer of energy into the higher harmonics.

With the input steepness of ε=0.1,the nonlinear wave effects and the wave-wave interactions in a wave train are no longer negligible,which causes some modification of the wave form and the wave spectrum,as presented in Fig.3.Second order harmonic waves can be found within the generated waves(see Fig.3(b)).

Fig.3(a) Free surface elevation of ε=0.1 at x=10m,——simulation,……linear solution;(b)Amplitude of Fourier series corresponding to waves of ε=0.1 at x=10m,——simulation,……linear solution

Fig.4(a)considers the free surface elevations resulting from the wave steepness of ε=0.2.The time series of the free surface elevation predicted by applying the linear wave theory are also shown in Fig.4(a).The discrepancies between the wave trains predicted by applying the numerical model and linear wave theory are increasing with increasing wavelength and are becoming significant for long waves.The outcome of the Fourier analysis regarding the result presented in Fig.4(a)is presented in Fig.4(b).A train of originally very narrow-banded waves changes its one-peak spectrum to a multi-peak one.Second order harmonic waves and higher order harmonic waves can be found within the generated waves.The wave profiles of the generated waves can not be predicted by the linear wave solution.There is evidently a need to introduce a more advanced theoretical solution to predict the generation and propagation of the generated waves in the wave flume.The second-order Stokes wave solution(Madsen,1971)will be applied to do it.

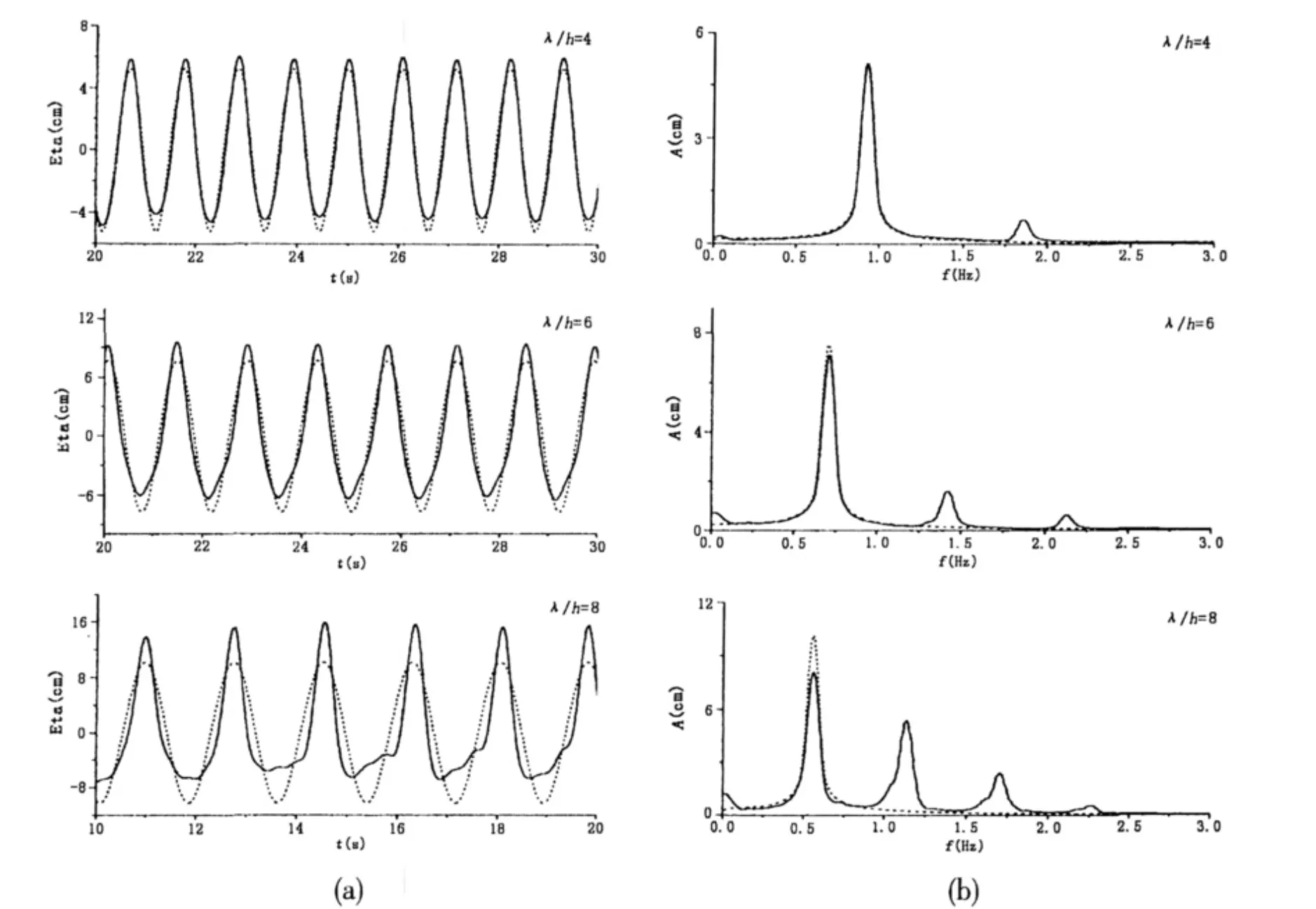
Fig.4(a) Free surface elevation of ε=0.2 at x=10m,——simulation,……linear solution;(b)Amplitude of Fourier series corresponding to waves of ε=0.2 at x=10m,——simulation,……linear solution

Fig.5 describes the comparison of the numerical wave profiles as presented in Figs.3 and 4 with those predicted using Eq.(8).The wave profiles of the generated waves with a wave steepness ε=0.1 are shown in Fig.5(a),while ε=0.2 shown in Fig.5(b).It can be found that the present numerical results are in good agreement with the second-order Stokes wave solution except for a wave steep ε=0.20 and λ/h=8.The case corresponds to an Ursell number Ur=32.64,which is beyond the limit of the validity of the theoretical solution(Eq.(8))presented by Madsen(1971).

The comparison of the Stokes second-order harmonic wave amplitudes between the numerical results and predicted using Eq.(8)are described in Fig.(6).For the case of λ/h=4,the numerical results agree well with those predicted using Eq.(8).For the case of λ/h=6,the sec-ond-order solution will underestimate the nonlinearity as the wavelength increases.For the case of λ/h=8,the preceding Stokes wave theory becomes less appropriate for the prediction of the generated waves for large wavemaker displacement and large Ursell number.This is because the second-order wavemaker solution is based on the Taylor-expansion about the wavemaker(x=0)that has a number of limitations.As the amplitude increases,the Ursell number will increase.The large Ursell number brings strong highorder nonlinear interactions in the wave train so that the generated waves change their wave profiles and the corresponding amplitude wave spectrums.A train of originally very narrow-banded waves changes its one-peak spectrum to a multi-peak one.This will be further discussed in the following physical model.

Fig.5(a) Free surface elevation of ε=0.1 at x=10m,——simulation,……predicted results using Eq.(8);(b)Free surface elevation of ε=0.2 at x=10m,——simulation,……predicted results using Eq.(8)

Fig.6 Amplitudes of the Stokes second-order waves:……predicted results using Eq.(8);(symbols)simulation:● λ/h=4,▼ λ/h=6,■λ/h=8

5 Comparisons with laboratory data

To assess the success of the numerical calculations discussed in section 4,physical model tests were performed in a wave tank of 50m long,3.0m wide and 1m deep at the State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,China.Comparisons between the laboratory data and the numerical calculations were undertaken.The wave tank was equipped with a piston-type wavemaker and a downstream wave-energy absorbing beach.Eight resistance-type wave gauges with 50Hz scan rate were used to measure water surface elevations.The first wave gauge was located at x=6m away from the wavemaker.The next 7 gauges with 2m distance between each other were to record the generated waves along the wave flume.Fig.7 is the sketch of the experimental setup.The experimental verification was restricted to the free surface elevation η（x,t）at the first wave gauge.Data recording started when the generated waves passed the last wave gauge and up to 10s of water-surface oscillations were recorded.

Fig.7 Wave flume

We have chosen to take the same kind of the initial conditions as in the above numerical calculations(see Tab.1).Laboratory experiments in the wave flume were conducted at the water depth h=0.4m.The measured time series of free surface elevations,the transform of wave components in the generated waves,and the measured amplitude wave spectrum were used to conduct verification of the numerical wave flume.

Figs.8-10 display the propagation of the generated waves along the wave flume resulting from the wave steepness ε=0.15.The plots show numerical and measured time series of the freesurface elevation and the corresponding amplitude wave spectrums,and the results are presented for the second,the fourth,and the sixth wave gauges.The amplitude wave spectrums are obtained by FFT to recorded time series.The comparison displayed in Figs.8-10 shows that the calculations agree well with the experimental data.There is a fairly good agreement between numerical and measured time series of the free surface elevations and the corresponding amplitude wave spectrums.For the case of λ/h=4,the generated waves are second-order Stokes waves of permanent form as presented by Madsen(1971)(see Fig.6).With the increasing wave length,the increased Ursell number causes some modification of the wave profile and the wave spectrum.For the cases of λ/h=6 and 8,the resulting wave generated by a sinusoidally moving wavemaker originally characterized by a one-peak spectrum is transformed to a multi-peak one.This is related with nonlinear wave-wave interactions in the generated wavetrains.The numerical wave flume predicts fairly well the multi-peak spectrums that are clearly visible in our analyzed cases(see Figs.8-10).The observed discrepancies between the calculations and experimental data are likely related with higher-order nonlinear interactions of the wave components that are not included in the numerical scheme.

Fig.8(a) Simulated and measured elevation for λ/h=4:——simulation,……experimental data;

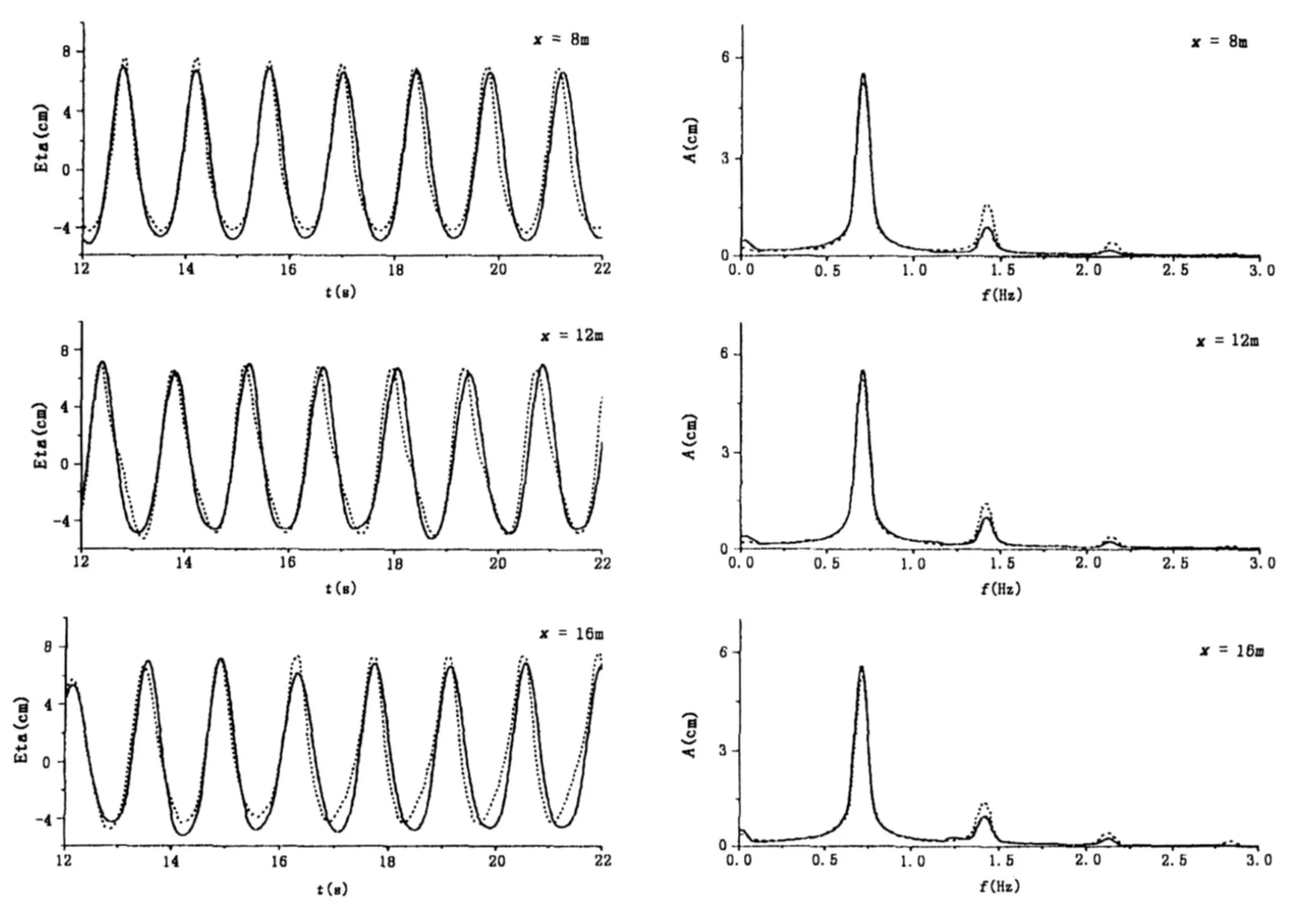
Fig.9(a) Simulated and measured elevation for λ/h=6:——simulation,……experimental data;

Fig.10(a) Simulated and measured elevation for λ/h=8:——simulation,……experimental data;(b)Simulated and measured amplitude for λ/h=8:——simulation,……experimental data

6 Conclusions

A fully-nonlinear numerical scheme has been implemented to predict the generation and propagation of nonlinear water waves in a wave flume,based on an enhanced high-order spectral method.By using additional potential technique,the free surface problem with a wavemaker is solved in a spectral manner by means of FFT.The incident waves are generated by adopting a second-order wavemaker theory.The fully-nonlinear boundary integral equations have been solved within a time-stepping procedure.The instantaneous wave elevations and potentials on the free surface are updated using the fifth-order Adams-Bashford-Moulton predictor-corrector adjustment method.

The derived numerical scheme is applied to predict the generation and propagation of transient nonlinear water waves in a wave flume.The main attention is paid to the wave profile,the amplitude wave spectrum,and the changes of wave profile and energy spectrum due to the wave-wave interactions in a wave train.The calculations are compared with the linear wave solution and the second-order Stokes solution.The results show that for waves of low steepness,the generation and the propagation of the generated waves can be predicted by linear solutions;with the increasing Ursell number till Ursell number=30,the numerical calculations of the wave profile and the amplitude wave spectrum are shown to be in good agreement with the second-order Stokes solution.

Laboratory experiments were conducted in a wave flume to verify the calculations.There is a fairly good agreement between the numerical and the experimental data.The numerical wave flume predicts fairly well the multi-peak spectrums.

[1]Benjamin T B,Feir J E.The disintegration of wave trains on deep water.Part 1:Theory[J].Journal of Fluid Mechanics.1967,27:417-430.

[2]Havelock T H.Forced surface-wave on water[J].Philosophical Magazine,1929,(8):569-576.

[3]Goda Y,Kikuya T.The generation of water waves with vertically oscillating flow at channel bottom[R].Rep.9.Port and Harbour Technical Research Institute,Ministry of Transortation,Japan,1964.

[4]Multer R H,Galvin C J.Secondary waves:Periodic waves of nonpermanent form[C].(Abstract)EOS 48,1967.

[5]Iwagaki Y,Sakai T.Horizontal water particle velocity of finite amplitude waves[C]//Proc.12th Conf.On Coastal Engineering.ASCE,Washington,DC,1970:309-325.

[6]Madsen O S.On the generation of long waves[J].J Geophys.Res.,1971,76:8672-8683.

[7]Sulisz W,Paprota M.Modeling of the propagation of transient waves of moderate steepness[J].Applied Ocean Research,2004,26:137-146.

[8]Sulisz W,Paprota M.Generation and propagation of transient nonlinear waves in a wave flume[J].Coastal Engineering,2008,55(4):277-287.

[9]Fenton J D,Rienecker M M.A Fourier method for solving nonlinear water-wave problems:Application to solitary-wave interactions[J].Journal of Fluid Mechanics,1981,118:411-443.

[10]Dommermuth D G,Yue D K P.A high-order spectral method for the study of nonlinear gravity waves[J].Journal of Fluid Mechanics,1987,184:267-288.

[11]West B J,Brueckner K A,Janda R S.A new numerical method for surface hydrodynamics[J].Journal of Geophysical Research,1987,92(11):803-824.

[12]Zhao X Z,Sun Z C.A high order spectral method and its application to nonlinear water waves[J].J Ship Mech.,2010,14(5).(Accepted)(in Chinese)

[13]Zhao X Z,Sun Z C,Liang S X.Focusing models for generating freak waves[J].Chinese Journal of Theoretical and Applied Mechanics,2008,40(4):447-454.(In Chinese)

[14]Clamond D,Fructus D,Grue J,Kristiansen Ø.An efficient model for three-dimensional surface wave simulations.Part II:Generation and absorption[J].J Comput.Phys.,2005,205:686-705.

[15]Agnon Y,Bingham H B.A non-periodic spectral method with application to nonlinear water waves[J].European Journal Mech.B/Fluids,1999,18:527-534.

[16]Le Touz'e D,Bonnefoy F,Ferrant P.Second-order spectral simulation of directional wave generation and propagation in a 3d tank[C]//In:Proc.12th Int.Offshore and Polar Engng.Conf.2002,3:173-179.

[17]Le Touz'e D,Bonnefoy F,Ferrant P.A fully-nonlinear high-order spectral 3d model for gravity waves generation and propagation[C]//In Proc.19th IWWWFB.Italy,2004.

[18]Bonnefoy F,Le Touz'e D,Ferrant P.Second order wavemaker theory:Prediction and control of free waves[C]//In:Proc.18th Int.Workshop on Water Waves and Floating Bodies.2003.

[19]Bonnefoy F,Le Touz'e D,Ferrant P.A fully-spectral 3D time-domain model for second-order simulation of wavetank experiments.Part A:Formulation,implementation and numerical properties[J].Applied Ocean Research,2006,28:33-43.

[20]Zakharov V E.Stability of periodic waves of finite amplitude on the surface of a deep fluid[J].Journal of Applied Mechanics and Technical Physics,1968,9:190-194.

[21]Larsen J,Dancy H.Open boundaries in short wave simulations-A new approach[J].Coastal Engineering,1987,7:285-297.