BP 神经网络在油脂颜色检测中的应用

高 杨，张慧宁

（黄河水利职业技术学院，河南 开封 475004）

0 引言

目前我国国家标准规定的和国际上通用的油脂颜色检测装置是罗维朋比色计[1]，而罗维朋比色计依靠人工目测读数，加之其滤色片组合色本身有一定的差异， 导致罗维朋值存在较大的主观误差。因此，开发客观测定油脂颜色的新方法非常必要。

近年来，出现的集成数字颜色传感器广泛地应用于色彩探测器和读取设备等领域， 进行色彩测量。其设计原理主要是依据人眼对三色响应的特性，在传感器上叠加窄带滤色片, 通过测量构成物体颜色的三基色的反射比率，实现颜色检测。 该类传感器直接输出数字量RGB 颜色值，可大大简化检测装置的电路，保证检测精度。 颜色传感器的RGB 测量值与罗维朋比色计测量系统属于不同的颜色表示方式，且不存在线性关系。 如果能找到合适的方法，建立二者的联系，则可以考虑使用集成颜色传感器取代传统罗维朋比色计， 作为油脂颜色检测的仪器，提高检测结果的客观性和准确性。

人工神经网络适用于解决很难精确建立数学模型的复杂问题, 并具有多维空间的非线性映射能力，在许多方面都有成功的应用。 本文探讨应用BP（Back Propagation，反向传输）神经网络建立集成颜色传感器检测得到的油脂颜色RGB 值与罗维朋黄值、红值的联系，消除油脂颜色检测中的主观因素。

1 BP 算法及网络结构的选择

1.1 BP 算法

BP 神经网络通过对系统输入输出样本对进行自动学习，能够以任意精度逼近任意复杂的非线性映射，因此，它由非线性普通变换单元组成[2]。 BP 网络是一种多层前馈神经网络，由输入层、隐含层和输出层组成，各层之间采用全互连方式，同一层之间不存在相互连接。 隐含层可以有一个或多个，一般采用单层就可以逼近任意非线性函数。

构造一个BP 网络，需要确定其处理单元——神经元的特性和网络的拓扑结构。 如果输入层、隐含层和输出层的单元个数分别为n、m、k，则图1 所示的3 层网络可表示为BP(n,m,k)。 利用该网络，可实现n 维输入向量X=(X1， …,Xn)T 到k 维输出向量O=(O1,…,Ok)T 的非线性映射。 输入层和输出层的单元数n、k 根据具体问题确定，而隐含层节点数m 的确定尚无成熟的方法， 一般可设定不同的m 值，根据训练结果来进行选择。

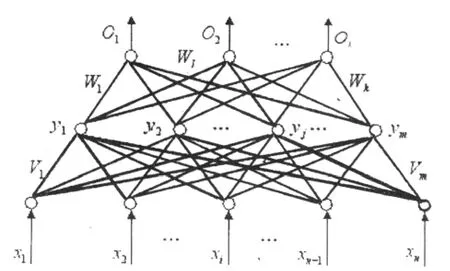
图1 BP 网络结构示意图Fig.1 BP network structure sketch

1.2 BP 神经网络结构和参数的选择

BP 神经网络能否建立油脂颜色RGB 值与罗维朋值的联系，关键在于如何设计网络的结构和参数。BP 神经网络的权值是通过使网络输出与样本输出之间的误差平方和达到期望值，不断调整训练出来的。 在网络设计过程中，涉及较多参数的确定，包括网络的层数、每层的神经元节点数、初始值的选取、学习规则、学习速率以及训练算法等。

网络结构的确定包括输入／输出节点、层数、每层的激活函数以及隐含层节点数。输入/输出节点是与样本直接相关的，如果样本格式已确定，则网络的输入/输出节点数即由样本确定。实验中需要建立的是油脂颜色的RGB 值与罗维朋红、黄值之间的映射关系,所以输入节点数应为3 个，输出节点数应为2个。 初始权值一般选取(-1,1)之间的随机数。 学习率η 和动量因子α 这两个参数需要通过试验来选择。

对神经网络的输入和输出数据进行一定的预处理，可以加快网络的训练速度。 网络的隐含层节点的作用函数选择的是对数Sigmoid 函数,考虑到对数Sigmoid 函数的输出值范围,需要对输入样本数据的R、G、B 值进行归一化处理, 使网络的输入值在(0,1)之间。 归一化方程为

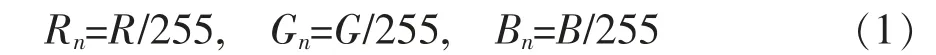
2 MATLAB 实现BP 网络

2.1 MATLAB 神经网络工具箱

在应用BP 网络解决实际问题的过程中,选择多少层网络、每层多少个神经元节点、选择何种传递函数、何种训练算法等,均无可行的理论指导,只能通过大量的实验计算获得。 这无形增加了研究工作量和编程计算工作量。 MATLAB 软件提供了一个神经网络工具箱(简称NNbox)，针对BP 神经网络的建立、传递函数的选择、网络的训练等,都有相应的函数，大大简化了编程工作。 网络初始化后，将输入和输出反复作用于网络，不断调整其权重和偏置量，以使网络的性能函数达到最小，从而实现输入输出间的非线性映射。 这里采用批变模式来训练网络。

2.2 训练参数的确定

根据上述分析，网络输入变量数n=3，输出变量数k=2，采用包含1 个隐含层的神经网络BP（3，m，2），输入层和隐含层的传递函数都为Sigmoid 型函数，输出层为purelin 型函数。当训练完成后，以油脂颜色的三基色R、G、B 作为输入值，网络的输出即为该颜色在罗维朋比色系统中对应的黄值和红值的近似值。

训练中，网络的收敛采用输出值Okp与实测值Op的平均绝对误差进行控制，其方法为

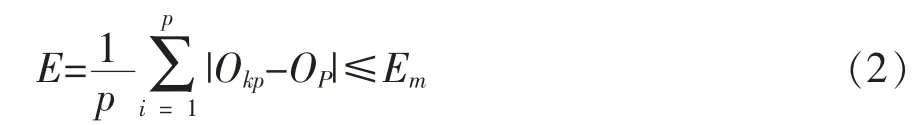
公式（2）中，训练精度Em为10-5。

隐含层节点数与所研究的具体问题有关，通常根据网络训练情况，采用试凑法确定[3]。 训练过程中， 为了寻求最佳隐含层节点数， 依次选择了10、15、24、32、48、64 来试验， 激活函数选用Sigmoid 型函数。 训练所得的网络结构参数与误差及收敛速度的关系如表1 所示。

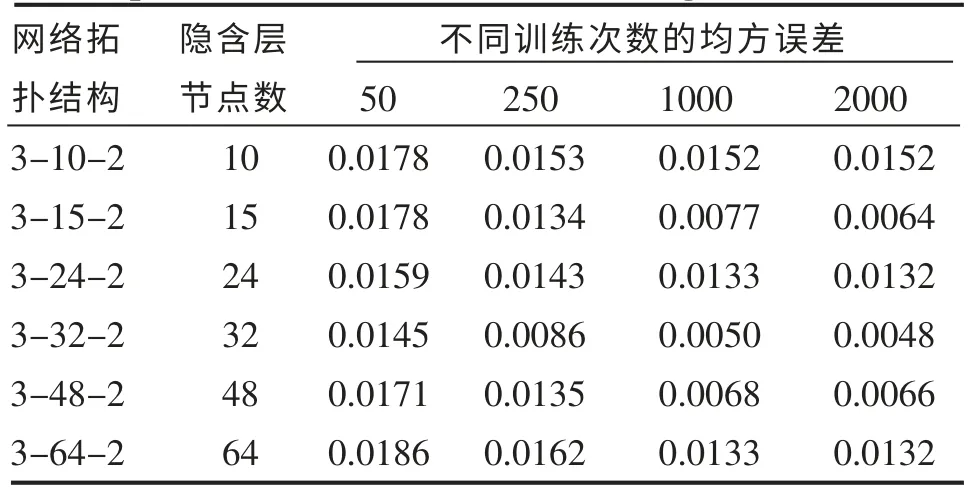
表1 部分网络结构参数与误差及收敛速度的关系Table 1 Relation of partial network structure parameter and error and convergence rate

从表1 可以看出，隐含层节点数并不是越多越好，也不是越少越好，而应当选择适当，这样网络才能在较少的训练次数下达到较高的训练精度。 综合上表中6 种网络结构隐含层节点数与误差关系来看，网络结构为3-32-2，即隐含层节点数为32 时，在训练次数为2000 次时， 其均方误差就相对稳定,且误差值最小(训练精度最高)。

3 BP 网络的训练及精度分析

3.1 训练样本数据的选取

在国家标准中，油脂的颜色标定是用罗维朋黄值和红值表示的，而且每一种油样在测定过程中的罗维朋黄值是固定的。 例如，在国家标准中，花生油的罗维朋黄值为25，芝麻油的罗维朋黄值为70。 试验选取罗维朋黄值20、25、30、35、70，对每一个固定的黄值下的红色1～20 滤色片的所有组合情况都采集RGB 值，作为训练网络的输入样本，以对应的罗维朋黄值、红值作为输出样本。 实验中，罗维朋滤色片的组合情况有100 种，选取其中的80 种用做训练网络的样本，其余20 种用来检验网络的精度。

3.2 BP 网络的训练

创建BP 神经网络，先选用普通训练函数中的批梯度下降训练函数（traingd）来训练该网络[4~5]。 采用的80 个样本数据对训练网络，输入为三维向量（罗维朋滤色片组合色的RGB 值），输出为二维向量（罗维朋滤色片组合色的红值和黄值）。 网络训练结果如图2 所示：

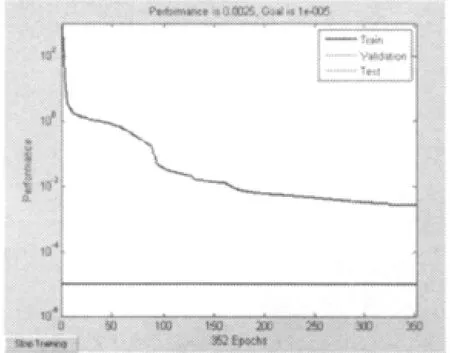
图2 traige 函数的网络训练误差Fig.2 Network training error of Traige function

从图2 中训练的结果来看， 在训练次数达到352次时，梯度达到最小值，训练停止，但误差只减小到0.0025，并没有达到训练要求的精度。这可能是由于误差达到了局部极小点所致。 因为BP 神经元的传输函数为非线性函数， 所以其误差函数往往有多个极小点。 在学习过程中， 如果误差先达到局部极小点，则在该点的梯度等于0。 此时，就无法继续调整权值和域值，学习过程结束，但尚未达到全局极小点。

由于经典BP 算法是在梯度法的基础上推算出来的，在实际应用中有一些不足，主要是收敛速度慢，网络易陷于局部极小，学习过程常发生振荡。因而考虑改用BP 改进算法—Levenberg-Marquardt 算法（简称LM 算法）。LM 算法是基于非线性最小二乘法的一种高效快速的学习方法， 可以提高多层前馈神经网络的学习效率及稳定性。 使用快速训练函数（trainlm）对上述80 个样本数据对重新训练。网络训练结果如图3 所示：

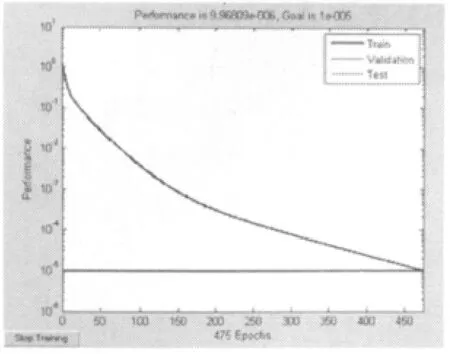
图3 LM 算法trainlm 函数的训练误差Fig.3 Training error of Trainlm function of LM algorithm

从图3 所示的训练结果来看，经过475 次循环，训练成功，网络精度达到要求。

3.3 BP 网络精度分析

利用sim（）函数对训练后的网络进行仿真，样本值与网络仿真输出值对比如表2 所示（样本量较大，表中只列出其中10 组对比数据）。

表2 样本值与网络仿真输出值的对比Table 2 Comparison of sample value and network simulation output value

从表2 中可以看出，对于黄值和红值，网络输出值与期望值之间的误差均未超过10-5，达到了预先要求，证明训练后的BP 网络是可行的。

4 结论

本文以MATLAB 软件为工具，以罗维朋比色计组合滤色片的RGB 值作为输入值，以罗维朋红值、黄值作为输出值，成功训练网络，并采用样本数据对网络精度进行了检验，结果表明，二者之间存在关联性。 BP 神经网络可以用于建立油脂颜色RGB 值与罗维朋黄值、红值之间的对应关系，从而初步建立颜色传感器检测值和传统油脂颜色检测值的联系，为油脂颜色检测方式的研究提供了一种新的参考。

[1] 孙凤霞，杜红霞.油脂颜色测定方法研究进展[J]. 中国油脂，2002，27（2）:7-9.

[2] 周开利， 康耀红. 神经网络模型及其MATLAB 仿真程序设计[M]. 北京：清华大学出版社，2005.69-90.

[3] 曹青松， 周继惠. MATLAB 在神经网络设计中的应用[J].华东交通大学学报2004，21（4）：86-88.

[4] 王巧华，任奕林，文友先. 基于BP 神经网络的鸡蛋新鲜度无损检测方法[J]. 农业机械学报，2006，37 （1）：104-106.

[5] 陈以新. MATLAB 的几则程序设计经验[J]. 计算机应用,1999，19（9）:54-56.