QNDE的核心科学与工程基础进展

Donald O.Thompson

（Iowa State University，IPRT 1915Scholl Road，Ames，IA 50011）

1 Introduction

It is necessary to define the terms that are used in this paper.While there is no universal consensus on term usage，Forney［1］defined the terms that are increasingly accepted and used herein.According to Forney，

· NDT refers to the development and application of the nondestructive test methods themselves

·NDI refers to the performance of inspections to established specifications or procedures using the NDT methods to detect anomalies

· NDE refers to the broad examination of materials，components，or assemblies to define，classify， and make qualitative， and eventually quantitative，measurements of anomalies in terms of size，shape，type，orientation，and hopefully materials strength and stress levels.

Following Forney，then，QNDE is defined to be the quantitative interdisciplinary engineering technology that deals with physical measurements for quality assurance.It is the technology that underlies NDE.

The purpose of this paper is to demonstrate that a science core for QNDE has indeed been constructed and that important engineering tools that follow exist.

2 Background

Nondestructive testing （NDT）had its formal beginnings in the U.S.during WW2 as an experiential，need－based technology.Its purpose was to assure that all war products and goods were without defect and of high quality.Because of the rush of World War II and，in contrast to other engineering technologies，NDT was reduced to practice without the benefit of the work of organized academic programs and a firm scientific base derived from a period of research and development. The first formal organization was the American Industrial Radiation and X－Ray Society which grew into the American Society for Nondestructive Testing （ASNT）that included an increased range of testing technologies.Means for this growth was provided by industry and its support organizations and federal high technology agencies such as the Department of Defense（DOD），the National Aeronautics and Space Administration（NASA），the Atomic Energy Commission（AEC）which has become the Nuclear Regulatory Commission（NRC）and the Department of Energy （DOE）. This approach produced an array of testing tools and techniques whose worth was proved in the war and following years in several high cost，high technology programs but was technically deficient of physical understanding of the measurements and their relation to materials and failure modes.

A selected summary of events that motivated the development of quantitative NDE （QNDE）from the 1950sto current times is shown in Table 1.In the following paragraphs comments are made that highlight three major points of guidance：the need to size defects，the need for improved flaw detectability，and the need for continued inspection in aging structures.

Table 1.A selected summary of events that motivated the development of quantitative NDE

Reading from bottom to top，most development in the 1950swas guided by a strategy from the war years– the“zero”defects strategy.This strategy declared that if any“indication”of a flaw were found，the product harboring the “indication”had to be removed from service.No criteria for flaw severity were available.This strategy was not only excessively costly but，as it turned out，also provided motivation for research which was aimed in the wrong directionhigher instrumental sensitivities and a greater ability to find smaller and smaller defects.

In the 1960－1970period，major changes took place.The first important change was the advent of fracture mechanics that introduced the idea of a critical flaw［2］.This was very important，for it said that flaws below a critical size were not important to safety and that fulfillment of a“zero defects”criterion was much more than needed for safety and acquired only at a much higher cost.Fracture mechanics and the recognition of critically sized flaws led to another significant change，i.e.the development of damage tolerant design.In contrast to the earlier safe life design practice and its “zero defects”inspection strategy，damage tolerant design permitted the existence of flaws in structures so long as they were below the critical size.Table 2shows the exceptionally large range of critical flaw sizes that characterizes various materials［3］.

Table 2.Estimates of critical flaw sizes in some metal and ceramic systems.After Thompson and Evans［3］（ⓒ1976IEEE）

In the 1970sand 1980swe learned that improved defect detectability was the next major milestone to be met.Figure 1shows two examples of military air disasters that emphasized this point.The left side shows a pylon failure in a C5aircraft due to a missed defect.The engine took off but the airplane is still sitting.The right side shows an inclusion in the wing of an F111aircraft that was missed and resulted in a crash with loss of life.It was reported that this inspection was done 11times and was missed 11times，both in the manufacturing cycle and in field inspection.

The period from 1980－1990brought into focus the third major need for improvement，i.e.the necessity and importance of continued and upgraded NDE inspections in all aging systems and infrastructures.A first example of this need was the tragic Aloha Airlines event in which the canopy of a commercial aircraft was torn off in flight with loss of life.It was later found that this event was traceable to a crack.A second major event was the crash of United Airlines flight 232at Sioux City due to an engine disc failure，again with the loss of many lives.

In the 1990sand the 2000schanges continued from lessons learned earlier.One of these was the need for scanning of large areas including structural health monitoring （SHM）and other condition based maintenance based strategies with simultaneous cost reduction.Industrial globalization lead to the extension of QNDE concepts world－wide through the establishment of the World Federation of NDE Centers and other mechanisms.This was an important step required to maintain a standard of quality world－wide.

It is important to understand the relationship between damage tolerant design and the imspection process.This is shown in Fig 2.As opposed to the earlier safe life design philosophy which supposes that no flaws exist，damage tolerant practice assumes that structures contain initial cracks that，if undetected，can grow in service to critical size at which point failure can occur.This is shown in the upper curve in which the growing crack size is plotted against service time of the part.An inspection is performed atT1；finding no crack or that the crack is still less than critical size，the service clock is reset and the part is restored to service.This process is repeated until the crack becomes critical and the part is removed from service.

The research community responded to these demands in the 1970swith the establishment of several major NDE research activities shown in Table 3.The NDE drivers are listed in the first column，and responses serving three different industry segments are shown in the remaining columns.In the U.S.，the aerospace industry was the focus of the Defense

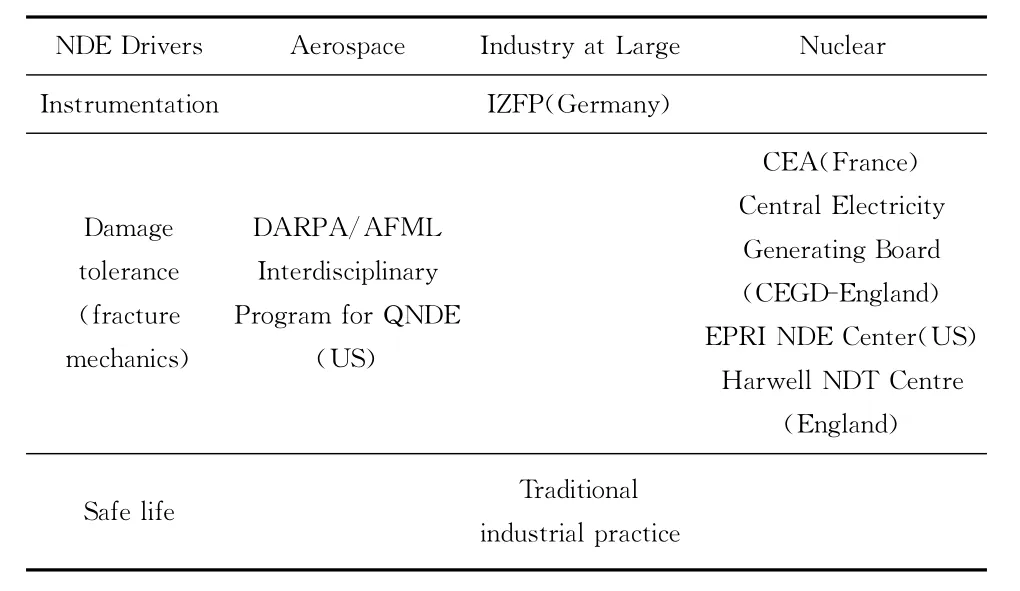
Table 3.Rand Dresponse to NDE needs

Advanced Research Projects Agency／Air Force Materials Laboratory （ DARPA／AFML ）Interdisciplinary Program for Quantitative Non Destructive Evaluation with emphasis upon finding ways to quantify flaw size and flaw detectability.Industry in Germany was served by the Fraunhofer Institute that formed the Fraunhofer Institute for Non－Destructive Testing（IZFP）with an emphasis upon the development of new techniques and instrumentation，while industry at large continued its ongoing research efforts that focused largely upon the improved instrumental sensitvity as required by safe life design practices.Several new activities were started that served primarily the emerging nuclear industry.These included the French Atomic Energy Commission（CEA）in France，the Central Electricity Generating Board （CEGB）and the Harwell NDT Centre in England and the Electric Power Research Institute（EPRI）NDT Center in the U.S.In addition to these major research activities that involved large numbers of investigators，various single investigator research efforts were also initiated.

3 Science Base

This paper will now focus on work initiated in the DARPA／AFML Program and extended by many others.The dual，broad objectives of the DARPA／AFML Interdisciplinary Program for Quantitative NDE are given，which shonld develop a new science／people base core that will meet the requirements for damage tolerant design and set a new path for NDE，and set the stage for the development of new engineering tools，which should initiate and develop QNDE meetings to help build a quantitative technology.The Air Force and DARPA were both aware that NDE deficiencies were severe and that research efforts needed to go back to fundamentals before reliable engineering tools could become available to address the needs of the new damage tolerant design.A third unwritten objective is also stated in the figure.The program manager was strongly encouraged by the sponsors to initiate efforts to develop a new people base that would be a part of the new quantitative technology.The current QNDE conference was started as a consequence to help build both the new peoplebase and the new quantitative technology.

Figure 3shows the building blocks that were deemed minimally necessary to form the core of an interdisciplinary science base for each NDE technology that would enable key parameters to be determined，i.e.flaw size，shape，and detectability［4］.They include the development of theories of flaw detection with various probe fields，inversion models with flaw sizing capabilities，and models for flaw detection leading to probability of detection （POD）relations，all with experimental confirmation.Success in developing these blocks would allow coupling to the materials engineering community to form the needed accept／reject criteria and to the physical mathematics groups to form PODs.As noted above，this set of building blocks is applicable to all NDE measurement techniques；however，the remainder of my comments will be focused upon advances in a standard ultrasonic test procedure since there isn't time and space to summarize the various techniques individually and they can't be done generically.It is to be noted，however，that progress similiar to that discussed here for ultrasonics has been accomplished for eddy currents and X－rays.

Figure 3.Generic NDE building blocks that form the core of an interdisciplinary science base.After Burte，Chimenti，Thompson，and Thompson［4］

In the following sections examples will be given of major advances that have been made in all the science base building blocks for the ultrasonic case.This is not intended to be，and certainly is not，a comprehensive survey，but one which shows that a sufficient number of working solutions has been obtained in all blocks to claim that a working science base literature has been developed for ultrasonics（and as noted above for other major technologies also）and is at work solving major problems.Many of these advances were seeded and done through the DARPA／AFML program but many were done by others，perhaps through contact with and contributions to this Conference.The reader is referred to the recent book by Schmerr［5］for a much more complete summary of the contributions to be discussed.

3.1 Theories of Interaction with Probe Fields

Much work has been done in the development of models that describe the fundamental interactions of the probe field with the flaw at the position of the flaw for the standard ultrasonic system shown in Fig 4［6］.These include transducer／field models，scattering models，a reciprocity model，and a measurement model that are reviewed briefly in this section.From these basics the size，shape，and detectability of the flaw can be determined.

Figure 4.Standard ultrasonic system that is utilized in model discussion.After Schmerr［6］

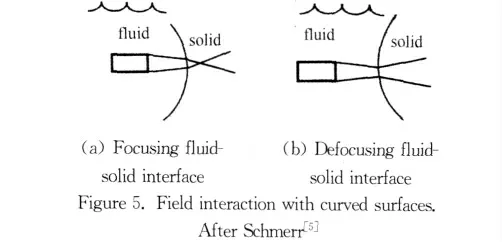
Models that describe the transducer field at any position in the test piece and their properties are given in Table 4and Fig 5.The Gauss－Hermite［7－9］，the multi－Gaussian［10－11］，and the boundary diffraction models［12－14］are all paraxial models.Other models have been developed that may be more detailed but also more computationally intensive than these［15－21］.The models describe fields generated by transducers of different shapes and fields and are calculated on the basis of external properties of the transducer（i.e.size and shape）rather than internal transducer structure such as is the case with older models due to Mason［22］and others.The right half of the figure shows model performance at both focusing and defocusinginterfaces，one of the practical considerations required of all transducers.

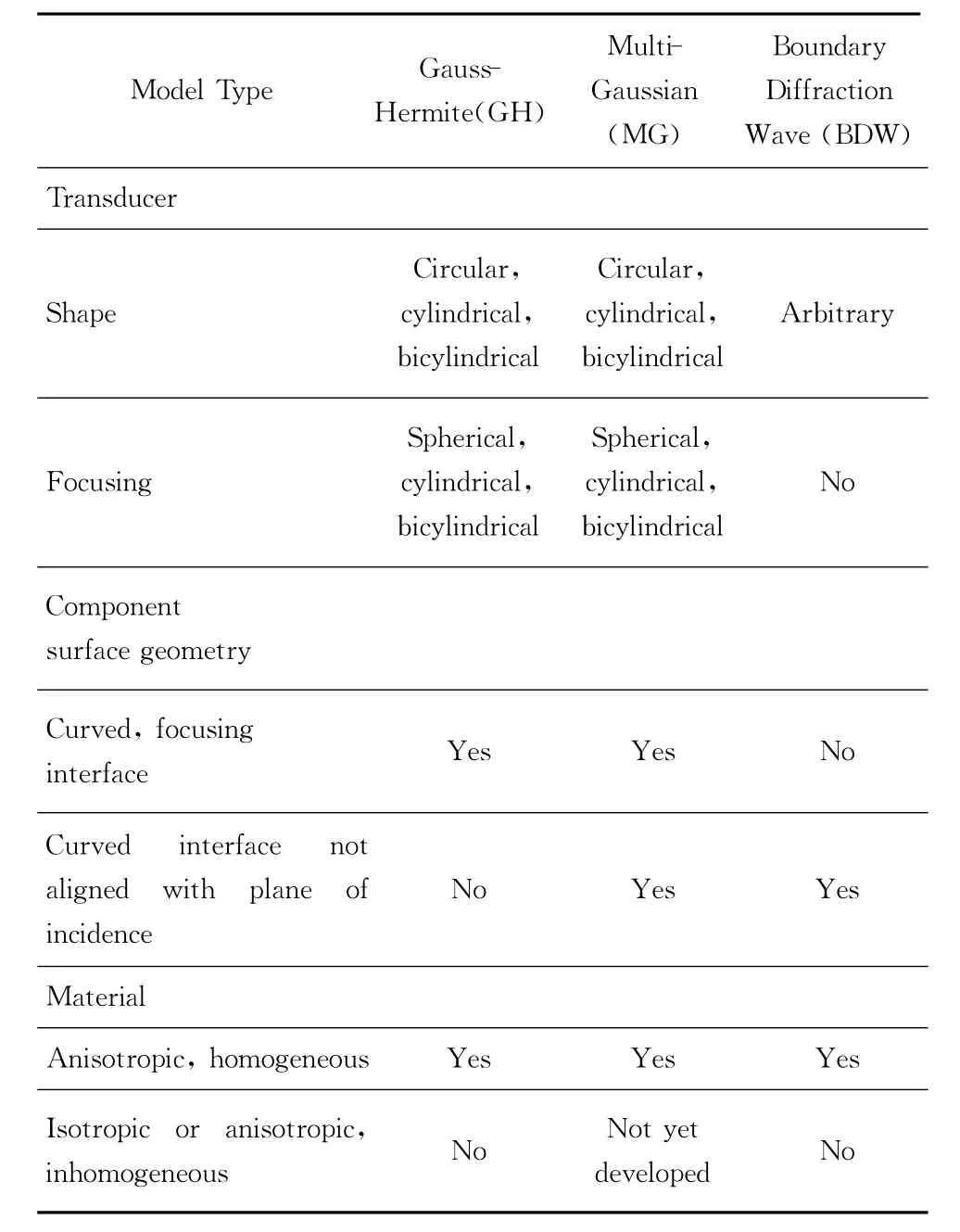
Table 4.Probe field／transducer beam models and some properties

After describing the generation and propagation of the probe fields，the interaction of the flaw with the probe field at the position of the flaw must be described.Here，a rich set of both analog and numerical scattering models and tools have been developed and are listed in Table 5and Fig 6.The analog models are approximate models and can be handled computationally fairly easily.Two limiting cases are shown in Table 5and Fig 6.The Kirchoff model［23－27］is a high frequency model that is widely used.As shown in the right half，the field at the flaw is taken to be the incident wave and the reflected wave at the point of contact with the flaw but reflections of the wave from the rear of the flaw are neglected.On the other hand，the Born model［28－32］is a low frequency model in which only the incident wave at the surface of the flaw generates the scattered wave.As yet，there is no model that is applicable in the mid frequency range. The geometrical theory of diffraction［33］is well known to many and is used often in the characterization of cracks.The earlier work of Ying and Truell［34］is an exact solution for the scattering by a spherical defect. It is not computationally easy and cannot be applied to other scattering shapes.

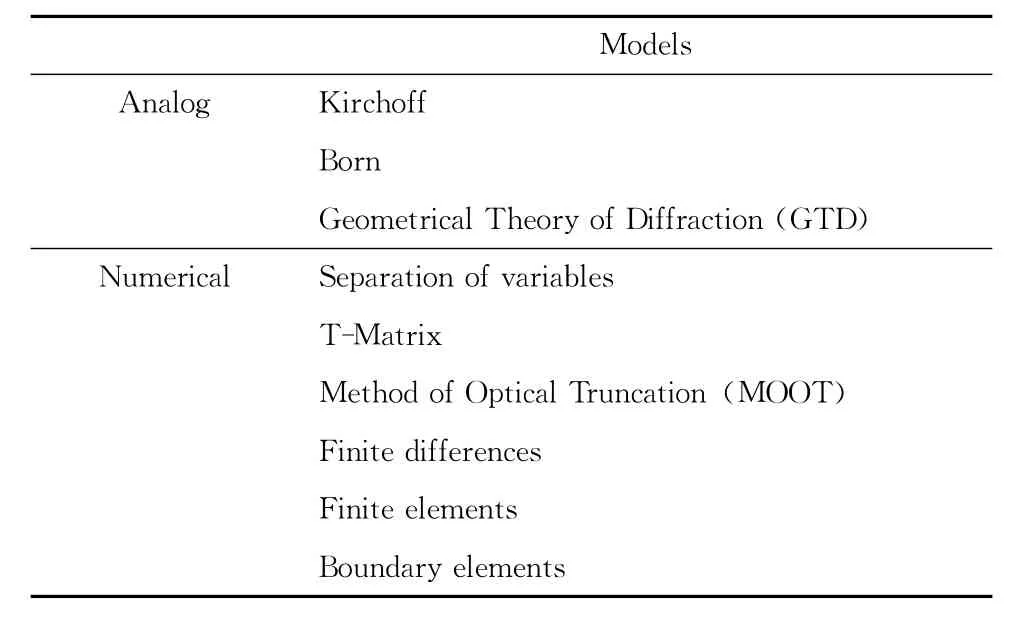
Table 5.Scattering amplitude models for the beam／flaw interaction

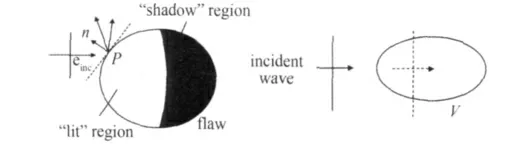
Figure 6.Interaction for the Kirchoff and Born approximations.After Schmerr［5］

Having the models described above and an additional way to measure the efficiency of the ultrasonic system，the results can be combined to yield a model of the entire measurement process，i.e.a“measurement model”.This combinatorial procedure was used by Tittman，Thompson，and Thompson［35］to form a “characteristic equation”in discussing ultrasonic standards and by Schmerr［5］in the context of the“measurement model”as defined above.A more elegant and rigorous approach that leads to similar results but doesn't depend upon the assumptions inherent in the combinatorial approach，i.e.a quasi plane wave condition at the position of the flaw and a flaw size small compared to the wavelength，was put forth by Auld in 1979［36］.Auld developed a general formulation based on electromechanical reciprocity that has been used widely in the development of today's“measurement models”.Specifically，he calculated the change in the cable （c.f.Figure 8）transmission coefficients due to the presence of the flaw in the system.

Figure 7.Measurement models results.In addition to labels in figure，ρ1is the density andνbis the ultrasonic velocity of the received mode in the solid medium，kbis the wavenumber of the received wave mode in the solid medium，ρ0is the density of the fluid medium，v0is the acoustic velocity in the fluid medium，and a is the transducer radius.After Thompson and Gray［11］

Using Auld's results， Thompson and Gray formulated the“measurement model”［37］for ultrasonics that is widely used in current day practice.Figure 7 shows their results.Notably，the measured system response is given by S in their equation and the flaw scattering amplitude is given by A.Other parameters in the equation are defined in the figure and figure caption.The appearance of both S and A in the same equation is useful（and also physically intuitive）since these are the two key parameters needed to satisfy the inspection requirements given earlier，i.e，A ，the scattering amplitude of the flaw that contains flaw sizing information and S，the measured signal amplitude.S is obtained by direct experimental procedures whereas A can be obtained by deconvolution，an inverse and usually difficult indirect procedure.

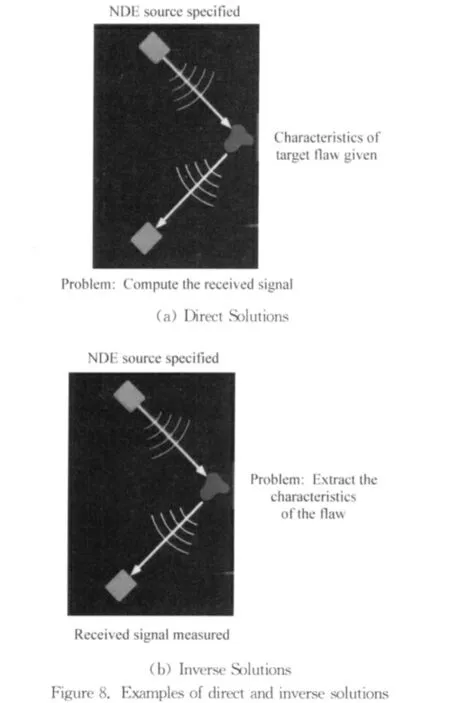
Fig 8is useful in physically understanding the concept of direct and inverse solutions.The direct solution is shown on the left side of the figure.In this case the source of the driving signal is known as are the details of the scattering flaw. With this information the signal S can be calculated or measured.The inverse problem is shown on the right half of the figure.Here the driving signal is known and the received signal is measured. A，the unknown scattering cross section，is then calculated.

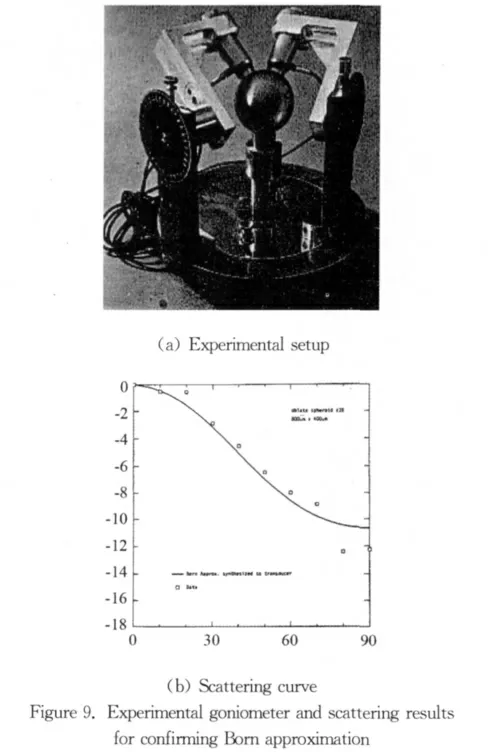
Experimental confirmation of modeling results and limits of model applicability have been an important part of the development of QNDE from its beginnings.It has become a welcome standard practice in QNDE research and resultant papers presented to note that theoretical work is nearly always followed by experimental confirmation in the well established scientific practice.Figure 9shows an example of some apparatus and results from early work by Tittman in confirming scattering results and limitations predicted by the Born approximation［38］.The apparatus was a precise goniometer and the samples were cleverly diffusion－bonded from two titanium halves，each half containing a carefully machined half of the test defect（e.g.spheres，ellipsoids，cracks）that were matched before bonding.Most measurements of this kind were pitch－catch measurements in which the scattering angles could be accurately measured and theoretical predictions checked.

3.2 Inversion Theories and Sizing Predictions

Information obtained from the flaw scattering amplitude in the measurement model is key in determining flaw size and shape that are required in damage tolerant design considerations.Various inverse solutions have been developed for small flaws using the Born and Kirchoff approximate models discussed earlier.These solutions are challenging because of the necessity of collecting much scattering data to avoid non－unique answers.It may be expected that use of these small flaw methods will increase with the advances in transducer array and signal processing technology.A variety of imaging，reconstruction，and characterization techniques and methods has also been developed to obtain size and shape data for larger flaws.Examples of these inverse procedures are given as belows.Imaging procedures are very attractive as an inverse technique whenever they can be used.

（1）Ultrasound

·Inversion of Tip Diffracted Signals（TOFD，RATT）

·Inverse Born Approximation

·Flaw Reconstruction

·SAFT in Anisotropic Media

·Imaging

· Materials Characterization

·Surface Characterization

（2）Eddy Currents

· Model－Based Crack Sizing

·Characterization of Coatings and Cladding

·Process Control of Extruded Materials

·Imaging（Scan and Array）

（3）X－Rays

·Imaging

3.3 Models for Flaw Detection and Probabilty of Detection（POD）

The direct solution S of the measurement model provides a way to fulfill the second major requirement cited earlier，i.e.，flaw detectability.Coupled with information that characterizes various kinds of noise distributions in samples and measurement systems such as electronic noise，surface roughness and grain scattering noise，and others that must be determined separately［5－6，39－46］，probability of detection（POD）models have been developed that predict the performance of the ultrasonic system and flaw detectability.Most models rely upon the results derived by Rice［47］for the envelope detection of a narrowband rectified signal in noise distributed normally.Such models usually result in asigmoidal shaped curve when plotted as a function of flaw size a，such as is shown in Fig.10in which the inflection point occurs at the critical flaw size.Regions of false reject and false accept are also shown.The left side of the figure gives expressions for the Probability of Detection and the Probability of False Alarm in which x is the flaw size，y is the signal amplitude，and yth is a noise threshold.Research in various aspects of the POD is intense at this time；the reader is encouraged to examine papers in these in the current and past volumes that relate to the subject.

Probability of Detection

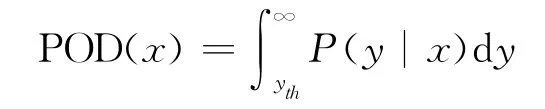
Probability of Nondetection

y…amplitude of signal

x…flaw size

（a）Forms of the probability of detection results

（b）The inflection point occurs at the critical flaw size

Figure 10.Calculation and illustrate of POD

3.4 Summary

Although research is never finished， the discussion in this section shows that a necessary working scientific base with continuity has been established in each of the boxes shown in Fig.7 associated with the science core.The base is sufficient to provide ways to obtain the inspection information（flaw size and shape，detectability）required by damage tolerant design considerations even though some of he answers are as yet difficult to implement.These include in particular inversion techniques which may be enhanced by future advances in transducer array technology and scattering models that are valid in the midrange.

4 Engineering Tools

Many new engineering tools and applications have been brought forward in recent years，but we will here focus on one major and very powerful tool– the simulator －that couldn't exist without，and is exclusive to，the structured fundamental modeling results described earlier in this paper.This tool has the potential for enhancing the role of NDE significantly in opening new opportunities，improving safety，and reducing manufacturing and operational costs of industrial products.The simulator is a concept and tool well known in a variety of technical endeavors.In the QNDE case，a simulator's purpose is to produce predictable QNDE results at the drawing board stage of a design as well as to permit parametric studies of inspection situations to be made.；it is constructed by joining some or all of the models discussed earlier with a way to describe the geometry of a part，such as a computer－aided design program.Several early QNDE simulators have been constructed that serve different purposes.Ultrasonic simulators include：CIVA－French Atomic Energy Commission（CEA）［48，49］；UTDefect－Chalmers University of Technology［50，51］；UTSIM–Center for NDE，Iowa State University［52，53］；GPSS，GP–IZFP，Saarbruchen［54－56］；EFIT– University of Kassel［57，58］；MSLM–Korea［59］.

The reader who is interested in details of the simulators is encouraged to read the references.A check will show that these simulators use different models in their structures and perform different operations.In addition to these ultrasonic simulators，simulation of eddy current and X－ray measurements have also been developed at the Center for NDE at Iowa State University（ECSIM and XRSIM）and at CEA where they are included in CIVA.

Many and varied applications have been identified for NDE simulators and many more can be expected.Some ultrasonic simulators that cover a wide range of interests in industry，education，and medicine are listed in as belows：

（1）Industrial

·Design of inspections

· Quantification of detection capabilities

· NDE inspectability during design

·Training

· Model assisted POD

（2）Research and Education

·Interpretation of experimental data

·Classroom and distance education

（3）Medical

·X－ray studies of dose effects

· Examination of therapeutic effects of UT on soft tissue

· Eddy current studies of heart valve fatigue damage

·POD concepts related to tumor detection

Industrially，applications listed bring QNDE to the front of the manufacturing process and provide quantitative assessments of inspection capabilities，both being long sought goals.Model assisted POD is a program of major current interest aimed at handling large statistical ensembles of components. Great opportunities for use in research and education exist as both and education and research tool. Some applications also exist in the medical as noted.

Figure 11.A CAD model of a turbine engine disc.After T.Gray［private communication］

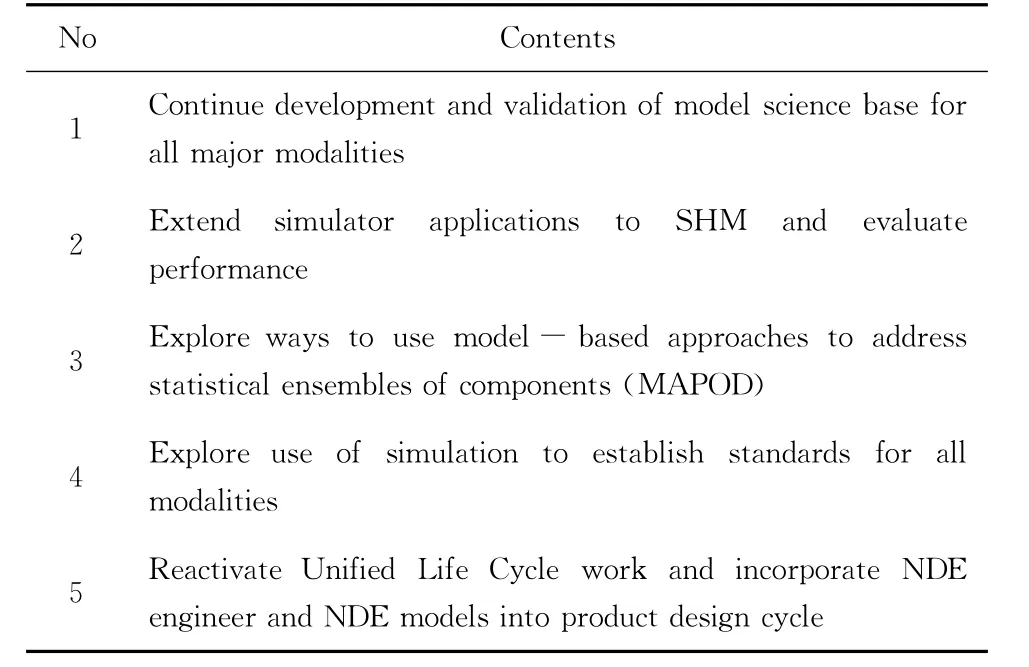
Table 6.Future directions that include both research and application

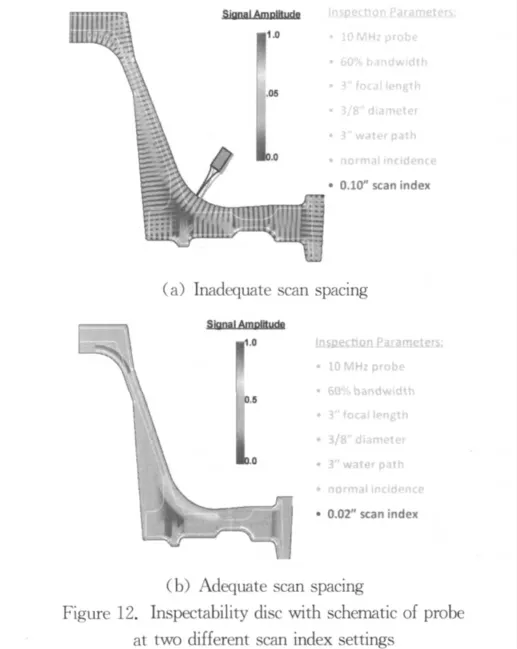
Figures 11 and Table 6 provide an excellent example due to T.Gray［60］of the use of simulation in the design of inspections and inspectability.Figure 11 is a CAD drawing of an engine turbine disc while details in Fig.12show a transducer set up to inspect the cross section of the disc with the transducer beam in the disc shown as a light colored area.Inspection parameters for two cases are shown on the left and right halves of the figure；they are the same with the exception of the scan index parameter，i.e.，the spacing between successive ultrasonic tests.On the left，labeled inadequate scan spacing（0.10”），it can be seen that there is a space between each of the inspections that is dark and therefore uninspected.On the right，labeled adequate scan spacing （0.02”），there is no dark space between beam patterns in the disc.In this case，the disc volume has been completely insonified and inspected This test can be very important when setting up the parameters to make an inspection.

5 Future Directions

As always，there are items of the science core that need to be completed and many new opportunities exist.A list of possible future directions is given in Table 6that includes both.Comments follow.

（1）We have a strong need to continue the validation of the model science base and the development of new models for all inspection modalities.Broad world wide validation of current models has been initiated by the World Federation of NDE Centers in a comparative benchmark program that is summarized below［61，62］.However，this is a small effort initiated and funded by the Federation that needs to be greatly extended.It is an important effort needed to make QNDE technology compatible on a worldwide stage.To the author's knowledge，this work has not been initiated but offers great promise.

NDE Benchmarks

· Benchmarks have included model－ model comparisons and comparison of models to experiments

· Benchmark activities have considered Ultrasonic，Eddy Current，Magnetic Flux Leakage，and Radiography problems

· Worldwide participation，including France，Germany，Sweden，Poland，Korea，China，India，Argentina，Brazil，and the USA

· Organized by the World Federation of NDE Centers.First benchmark session held at RPQNDE Brunswick，Maine meeting in 2001

（2）It seems obvious that simulation techniques coupled with CAD，POD，and other model capabilities will be very useful in the engineering design，initial evaluation，and implementation of big system NDE such as structural health monitoring.For example，simulation provides the capability to test different sensors， different sensor locations and number required，and optimize POD results in different geometries all at the“drawing board”.

（3）Serious major problems exist in the inspection of complex aging structures.For example，current practice requires the fabrication of many samples to validate an inspection procedure on a given part.Given multiple similar structures and multiple structures of various kinds，it is easy to see that the inspection costs and times rapidly become unmanageable.It may be that computer simulation coupled with some experimental work could provide significant advantages. Model assisted POD （MAPOD），a curently active project，is addressing this issue.

（4）Computer based simulations should find a welcome role in improving significantly reference standards for all NDE modalities.The use of model based results，once confirmed in general，can be used to provide specific predictions for a given measurement against which the test system may be compared.This procedure would do away with the need for test blocks that depend upon material properties （inherently included in the test block material）that often make the test blocks irreproducible（from time to time and place to place）for standards purposes.

（5）It is important to re－establish the Unified Life Cycle Engineering（ULCE）activity that the Air Force initiated some time ago［63－65］.This concept，shown anecdotely in Fig.13，envisions that the QNDE engineer can now take a seat at the designer's“table”on an equal basis with all the other disciplinary engineers involved in product design.The QNDE engineer has，for the first time，a full set of model based tools with which to interact with the other engineers －i.e，CAD designer programs，stress analysis programs，new materials and properties models，failure mechanics and reliability models，and cost and models. The concept integrates and incorporates original design， operational， and maintenance schedules such as structural health monitoring and conditional based monitoring all at the design table.

Figure 13.The new QNDE engineer seated at the designer's table

6 Summary

Although it has been more than a generation since QNDE research began with a specific focus to produce both a new quantitative NDE technology that meets the requirements of damage tolerant design and a complement of new QNDE researchers and engineers who will promote the field，even a partial summary such as given here and the continuing excellent audience at QNDE shows that the time has been well spent.So，in summary，

· A core science base has been demonstrated including theory with experimental confirmation.

·The science base forms a powerful platform for new engineering tools e.g.simulations and a wide range of applications，

· Development of a model －based science core raises NDE from an experiential technology to a predictive engineering science with a seat at the designer's table.

· The science core development has benefited immensely from attendee contributions to QNDE emanating from the DARPA／AFML seed.

Acknowledgement：The author wishes to acknowledge with sincere thanks the support and friendship of Dr.R.Bruce Thompson who has provided technical leadership in all the scientific and technical development aspects of QNDE.He also wishes to thank many others for their participation over many years，especially Drs.George Alers，Otto Buck（deceased），B.Tittmann，C.Fortunko （deceased），Neil Paton，A.Evans（deceased），Lester Schmerr，Jr.，J.Rose，Dale Chimenti，Lisa Brasche，John Moulder（deceased），T.Gray，J.Gray，R.Roberts，F. Margetan， D. Hsu， Norio Nakagawa，J.Krumhansl（Cornell University），Jan Achenbach（Northwestern University），Robert L.Thomas（Wayne State University），R.White，（UC Berkeley），B.Auld （deceased）and G.Kino（Stanford University）and contributors to and attendees at the QNDE Conference，members of the World Federation of NDE Centers and loyal staff members from the Rockwell International Science Center and the Center for NDE.No acknowledgement would be complete without noting the excellent guidance that the DARPA／AFML program received from Dr.Harris Burte，Mr.Don Forney，and Dr.Michael Buckley at the AFML and Dr.Ed van Reuth at DARPA at its initiation and in the formative years，and continuing guidance from various program monitors including Dr.D.E，Chimenti，now at Iowa State University.Neither would it be complete without acknowledging the introduction to the changing NDT environment in the 50'and 60'and mentoring provided to various program researchers by Mr.Ed Caustin，Director of the B－1 Quality Assurance Program at North American Rockwell.The B－1aircraft was the first major military system built to damage tolerant design specifications.The QNDE Conference is indebted to the Air Force，ASNT，NASA，NSF，and numerous industrial partners for their long term support.

［1］ Forney DM. USAF NDE Program－Requirement for Technology Transaction［R］.AFML－TR－TI－44，1975－1976：220.

［2］ Anderson TL.Fracture Mechanics：Fundamentals and Applications［M］.Boca Raton，Florida：CRC Press，2005.

［3］ Thompson RB，Evans AG.IEEE Transactions on Sonics and Ultrasonics，1976，SU23（5）：291.

［4］ Burte HM，Chimenti DE，Thompson RB，et al.The Middle Ground of the NDE R＆D Spectrum［G］.Review of Progress in Quantitative NDE.New York：Plenum Press，1978（2A）：7－18.

［5］ Schmerr，Lester W Jr.Fundamentals of Ultrasonic Nondestructive Evaluation －A Modeling Approach［M］.New York：Plenum Publishing Company，1998.

［6］ Schmerr LW， Song SJ. Ultrasonic Nondestructive Evaluation Systems– Models and Measurements［M］.New York：Springer，2007.

［7］ Newberry BP.Paraxial Approximation for Ultrasonic Beam Propagation in Liquid and Solid Media with Application to Nondestructive Evaluation［D］.Ames，Iowa：Iowa State University，1988.

［8］ Newberry BP，Thompson RB.A Paraxial Theory for the Propagation of Ultrasonic Beams［J］.Acoust Soc Am，1989（85）：2290－2300.

［9］ Newberry BP，Thompson RB，Lopes EF.Development and Comparison of Beam Models for Two－Media Ultrasonic Inspection［G］. Review of Progress in Quantitative NDE.New York：Plenum Press，1987（6A）：639－647.

［10］ Wen JJ，Breazeale MA.A Diffraction Beam Expressed as the Superposition of Gaussian Beams［J］.Acoust Soc Am，1988（83）：1752－1756.

［11］ Huang D，Breazeale MA.A Gaussian Finite－Element Method for Description of Sound Diffraction［J］.Acoust Soc Am，1999（106）：1771－1781.

［12］ Schmerr LW，Lerch TP，and SedovA.Modeling the Propagation of Ultrasonic Sound Beams through General Curved Surfaces［G］.Review of Progress in Quantitative NDE.，New York：Plenum Press，1997（16A）：845－851.

［13］ Lerch TP.Ultrasonic Transducer Characterization and Transducer Beam Modeling for Applications in Nondestructive Evaluation［D］.Ames，Iowa：Iowa State University，1996.

［14］ Schmerr LW， Lerch T，Sedov A. A Boundary Diffraction Wave Theory and its Application to Ultrasonic NDE［G］.Review of Progress in Quantitative NDE.New York：Plenum Press，1994（13A）：69－74.

［15］ Ludwig RL，Moore D，Lord W.Transducer Models for the Finite Element Simulation of Ultrasonic NDT Phenomena［G］.Review of Progress in Quantitative NDE.New York：Plenum Press，1987（6A）：649－655.

［16］ Ludwig R，Lord W.Finite Element Study of Ultrasonic Wave Propagation and Scattering in Aluminum［J］.Mat Eval，1988（46）：108－113.

［17］ Lord W，Ludwig R，You Z.Developments in Ultrasonic Modeling with Finite Element Analysis［J］.Nondestr Eval，1990（9）：155－160.

［18］ Goswami PP，Rudolphi TJ，Roberts RA，et al.Ultrasonic Transmission through a Curved Interface by the Boundary Element Method［G］.Review of Progress in Quantitative NDE，New York：Plenum Press，1991（10A）：193－200.

［19］ Guo QC，Achenbach JD.Radiation of Ultrasound into an Anisotropic Solid［J］.Ultrasonics，1995（33）：449－456.

［20］ Marklein R， Barmann R， Langenberg KJ. The Ultrasonic Modeling Code EFIT as Applied to Inhomogeneous Dissipative and Anisotropic Media［G］.Review of Progress in Quantitative NDE，New York：Plenum Press，1995（14）：251－258.

［21］ Marklein R， Langenberg KJ， Klaholz S，et al.Ultrasonic Modeling of Real－Life Situations：Applications and Further Developments［G］.Review of Progress in Quantitative NDE.New York：Plenum Press，1996（15）：57－64.

［22］ Mason WP.Physical Acoustics，Vol.1－Part A［M］.New York：Academic Press，1964.

［23］ Neubauer WG.A Summation Formula for Use in Determining the Reflection from Irregular Bodies［J］.Acoust Soc of Am，1963（35）：279－285.

［24］ Johnson DM.Model for Predicting the Reflection of Ultrasonic Pulses from a Body of Known Shape［J］.Acoust Soc of Am，1976（59）：1319－1323.

［25］ Haines NF，Langston DB.Reflection of Ultrasonic Pulses from Surfaces［J］.Acoust Soc Am，1980（67）：1443－1454.

［26］ Avestas JS.Physical Optics Method in Electromagnetic Scattering［J］.Math Phys，1980（21）：290－299，.

［27］ Sedov A，Schmerr LW.Pulse Distortion and the Elastodynamic Kirchoff Approximation for Cracks：the Direct and Inverse Problems［J］.SIAM J Appl Math，1987（47）：1201－1215.

［28］ Gubernatis，JE，Domany E，Krumhansl JA，et al.The Born Approximation in the Theory of Scattering of Elastic Waves by Flaws［J］.Appl Phys，1997（48）：2812－2819.

［29］ Gubernatis JE，Domany E，Krumhansl JA.Formal Aspects of the Theory of Scattering of Ultrasound by Flaws in Elastic Materials［J］.Appl Phys，1997（48）：2804－2811.

［30］ Hudson JA， Heritage JR.The Use of the Born Approximation in Seismic Scattering Problems［J］.Geophys J Royal Astron Soc，1981（66）：221－240.

［31］ Rose JH， Richardson JM. Time Domain Born Approximation［J］.Nondestructive，1982（3）：45－53.

［32］ Rose JH. Elastic Wave Inverse Scattering in Nondestructive Evaluation［J］.Pure Appl Geophys，1989（131）：715－739.

［33］ Achenbach JD，Gautesen AK， McMaken H.Ray Methods for Waves in Elastic Solids［M］.Boston：Pitman Books Ltd，1982.

［34］ Ying CF，Truell R.Scattering of a Plane Compressional Wave by a Spherical Obstacle in an Isotropic Elastic Solid［J］.Appl Phy，1956（27）：1086－1097.

［35］ Tittmann B，Thompson DO，Thompson RB.Standards for Quantitative NDE［C］.Proceedings of Symposium on NDT Standards， 1976， Nondestructive Testing Standards—A Review （STP 624）. Philadelphia：American Society for Testing and Materials，1977.

［36］ Auld BA. General Electromechanical Reciprocity Relations Applied to the Calculation of Elastic Wave Scattering Coefficients［J］.Wave Motion，1979（1）：3－10.

［37］ Thompson RB，Gray TA.A Model Relating Ultrasonic Scattering Through Liquid－Solid Interfaces to Unbounded Medium Scattering Amplitudes［J］.Acoust Soc Amer，1983（74）：140－146.

［38］ Tittmann BR，Elsley RK.Experimental Measurements and Interpretation of Ultrasonic Scattering by Flaws［C］.Proceedings of the ARPA／AFML Review of Progress in Quantitative NDE： Science Center， Rockwell International，AFML－TR－78－55，1978：26－35.

［39］ Thompson RB，Margetan FJ.Use of Elastodynamic Theories in the Stochastic Description of the Effects of Microstructure on Ultrasonic Flaw and Noise Signals［J］.Wave Motion，2002（36）：347－365.

［40］ Oakley CG.Calculation of Ultrasonic Transducer Signal－Noise Ratios Using the KLM Model［J］.IEEE Trans Ultrasonics，Ferroelectrics，and Frequency Control，1997（44）：1018－1026.

［41］ Yalda－Mooshabad， Margetan FJ， Thompson RB.Applying the 2D Random Walk Formalism to Predict Ultrasonic Grain Noise Distributions［G］.Review of Progress in Quantitative NDE，New York：Plenum Press，2002（13B）：347－365.

［42］ Ogilvy JA.Theory of Wave Scattering from Random Rough Surfaces［M］.Bristol，England：Institute of Physics Publishing，1991.

［43］ Margetan FJ，Thompson RB.Microstructural Noise in Titanium Alloys and its Influence on the Detectability of Hard–Alpha［G］.Review of Progress in Quantitative NDE，New York：Plenum Press，1992（11B）：1717－1724.

［44］ Rose JH.Ultrasonic Backscatter from Microstructure［G］.Review of Progress in Quantitative NDE，New York：Plenum Press，1992（11B）：1677－1684.

［45］ Rose JH. Theory of Ultrasonic Backscatter for Multiphase Polycrystalline Solids ［G］. Review of Progress in Quantitative NDE.New York：Plenum Press，1993（12B）：1719－1726.

［46］ Meeker WQ，Chan V，Thompson RB，et al.A Methodology for Predicting Probability of Detection for Ultrasonic Testing ［G］. Review of Progress in Quantitative NDE.Melville，NY：American Institute of Physics，2001（20B）：1972－1978.

［47］ Rice SO.Mathematical Analysis of Random Noise［J］.Bell Syst Tech Journ.1945（24）：46－156.

［48］ Calmon P.Recent Developments in NDT Simulation［C］.Proc World Congress on Ultrasonics，2003：443－446.

［49］ Lhemery A，Calmon P，Lecoeur－Taibi，et al.Modeling Tools for Ultrasonic Inspection of Welds［J］.NDT＆E International，2000（33）：499－513.

［50］ Bostrom A，Wirdelius H.Ultrasonic Probe Modeling and Nondestructive Crack Detection［J］.Acoust Soc Am，1995（97）：2836－2848.

［51］ Bostrom A. A Review of Hypersingular Integral Equation Method for Crack Scattering and Application to Modeling of Nondestructive Evaluation［J］.Appl Mech Rev，2003（56）：383－405.

［52］ Turnbull A，Garton M.Ultrasound Ray Tracing in Arbitrary Complex Geometries［G］.Review of Progress in Quantitative NDE.New York：Plenum Press，1995（14A）：1105－1110.

［53］ Garton M.Refining Automated Ultrasonic Inspections with Simulation Models［G］.Review of Progress in Quantitative NDE.New York：Plenum Press，1998（17B）：1825－1829.

［54］ Spies M，Batra NK，Simmonds KE，et al.Numerical Modeling and Imaging of Three Dimensional Transducer Fields in Anisotropic Materials［G］.Review of Progress in Quantitative NDE.New York：Plenum Press，1997（16A）：837－851.

［55］ Spies M，Kroning M.Elastic Wave Field Modeling for Arbitrarily Oriented Orthotropic Media［G］.Review of Progess in Quantitative NDE.New York：Plenum Press，1998（17B）：1163－1170.

［56］ Spies M.Transducer Field Modeling in Anisotropic Media by Superposition of Gaussian Base Functions［J］.Acoust Soc Am，1999（105）：633－638.

［57］ Marklein R.NDT－Related Quantitative Modeling of Coupled Piezoelectric and Ultrasonic Wave Phenomena［C］.Proc 7thEuropean Conference on NDT，1998：1－44.

［58］ Marklein R，Langenberg K，Mayer K.EFIT Simulations for Ultrasonic NDE［J］.NDT net，2003，8（3）：1－6.

［59］ Yim H，Baek E.Two－Dimensional Numerical Modeling and Simulation of Ultrasonic Testing［J］.Journ of the Korean Soc for NDT，2002（22）：649－658.

［60］ TA Gray.private communication.

［61］ Udpa SS，Thompson DO. Modeling of Benchmark Problems［G］.Review of Progress in QNDE.New York：AIP，Melville，2001（21B）：1891－1893.

［62］ Thompson RB. Ultrasonic Benchmarking： Past Programs and Future Goals［G］.Review of Progress in QNDE，New York：AIP，Melville，2004（23B）：1529－1536.

［63］ Burte HM， Chimenti DE. Unified Life Cycle Engineering：An Emerging Design Concept［G］.Review of Progress in Quantitative NDE，New York：Plenum Press，1986（6B）：1797－1812.

［64］ Schmerr LW， Thompson DO. Incorporating Inspectability into Design：The New Role of NDE in Concurrent Engineering ［C］. Proc ASME／NDE Engineering Div.Topical Conference，“NDE's Role in Concurrent Engineering，”SanAntonio，Texas，1992：22－23.

［65］ Schmerr LW，Thompson DO.NDE Models and Design－A Unified Life Cycle Engineering Approac［G］.Review of Progress in Quantitative NDE New York：Plenum Press，1994（13B）：2183－2190.