连续时间的均值-方差组合选择及其有效前沿*

郭子君 刘道海

(华南农业大学理学院1) 广州 510640) (武汉理工大学理学院2) 武汉 430074)

近些年来对最优投资策略的研究已经很多,投资对象标的价格假设为一个连续的扩散过程——几何布朗运动[1-2].假设存在主力(机构)交易者时讨论了具有异常波动市场的最优投资与消费策略[3].连续时间投资问题研究常用的方法有两种:动态规划方法与随机最优控制方法.如果市场模型的系数是确定性的函数,这两种方法能较好地用于最优投资与消费的某些问题研究中.如果市场模型的系数是随机变化时,用以上方法研究投资组合问题变得十分困难[4].

本文讨论由Brown运动趋动的系数随机变化的市场模型中投资组合问题.利用D.Duffie[5]和E.Pardoux和S.Peng[6]建立的倒向随机微分方程理论及J.Ma和Yong J[7-8]的正倒向随机微分方程理论,在均值-方差投资组合框架下,得到了相应的有效投资组合以及投资组合的有效前沿.

1 假设与市场模型

上的范数;C([0,T];X)={f(·)∣f:[0,T]→X;在[0,T]上连续}.金融市场中的不确定性因素用

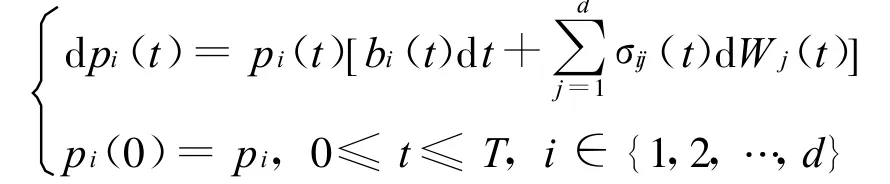
记b(t)=(b1(t),b2(t),…,bd(t))T,σ(t)=(σij(t))d×d.考虑利率变化是随机过程的情形,假定适应的无风险债券的利率随机过程r(t)∈C([0,T];R),适应的期望瞬时收益率随机过程向量b(t)∈C([0,T];瓗d)适应的扩散系数随机过程矩阵 σ(t)∈C([0,T];瓗d×d),而且d 阶方阵 σ(t)σ(t)T非奇异且满足条件 σ(t)σ(t)T≥δI,a.s ∀t∈[0,T],其中δ是某个正数,I是d阶单位矩阵.概率空间(Ω,F,{F t}t≥0,P)上的 d 维瓗d值Brown运动W(t)=(W1(t),W2(t),…,Wd(t))T表示,其中由W(t)生成的含所有零概率事件的递增σ-域流{F t}是经济参与者感知的信息流.

考虑交易可连续进行且无磨擦的完全金融市场,设市场上有d+1种标的资产,其中一种为无风险债券,价格 p0(t)满足方程

假设投资者的初始财富为x0,时刻t的财富为x(t).投资者在t时刻投资第i种风险资产的投资额为 πi(t),称 π(t)=(Π1(t),π2(t),…,πd(t))T为投资组合过程,如果它是取值于瓗d关于F可料的过程且有∫T0‖π(t)‖2d t＜ ∞,a.s;所有投资组合过程的集合记为Π.

对于容许卖空的市场,投资者在一个有限时域[0,T]内连续地进行投资,设初始财富为x0＞0,t时刻的财富x(t)满足如下随机微分方程

式中:l d=(1,1,…,1)T∈瓗d

定义 称投资策略 π(t)为容许的,若F t适应的投资组合过程π(t)确定的方程式(1)的解 x(t)≥0(0≤t≤T)a.s,容许投资策略的全体记为A.

令 θ(t)=(θ1(t),θ2(t),…,θd(t))T是如下矩阵方程的解

按以下步骤构造新的概率测度.记Z(t)是如下随机微分方程的解

根据 K ·Itˆo 公式有

定义新的概率测度¯P=Z(T)P,由Girsanov定理可知,过程是关于¯P-F t的Brown运动.因此,关于财富过程有如下表示

2 均值-方差组合选择

在连续时间情形,动态规划方法与随机最优控制理论是解决此类问题的2种主要方法.利用倒向随机微分方程理论,讨论系数是随机过程的扩散标的价格过程下均值-方差组合选择问题.

对于最优化问题

如果存在投资策略π(t)*使得式(1)对应的财富过程是最优化问题(B)的解,易知也是最优化问题(A)的解并且有E()=∈.关于最优化问题(B)与(C),有如下命题.

命题2.1 如果存在投资策略π(t)*使得式(1)对应的财富过程是最优化问题(B)的解,则π(t)*是最优化问题(C)当λ=1+2θE()时的解.

如果均值-方差组合选择问题(A)存在最优投资策略π(t)*,可以通过求解最优化问题(C)当λ=1+2θE(x*T)时的最优策略来得到.依据最优化问题的这种嵌入技术,重点讨论系数是随机过程的扩散标的价格过程下最优化问题(C)的最优策略.

设U(x)=θx2-λx.其中:常数 θ＞0,易知U(x)为上凸函数.令V(y)为U(x)的反函数,最优化问题(C)可表示为E[U(xT)].其中-∞＜λ＜+∞.设ξ(t)=c β(t)Z(t),0 ≤t≤ T,考虑函 数 φ(y)=¯E[β(T)V(yζ(T))] 和 其 反 函 数 ψ(x), 显 然φ(ψ(x))= x. 由 以 上 定 义 可 得

定理2.2 设投资者的初始财富为 x0,θ＞0,υ(t)1×d 是满足M t=M0+β(s)υ(s)dW¯(s)的可料适应过程,其中Mt=E¯[(β(T)V(ψ(x0)×(T))/.则最优化问题(C)存在惟一最优投资策略π(t)*=[υ(t)(σ(t))-1]T,并且在此策略下的最终财富为

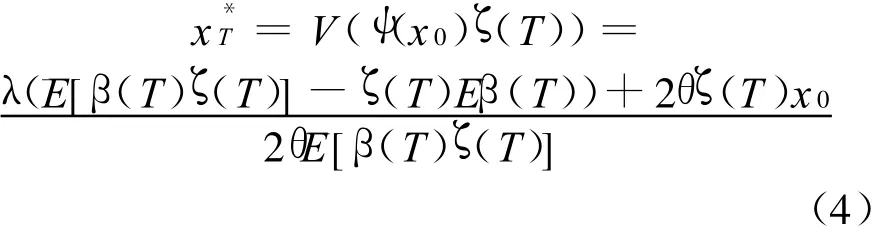
证明1 如下倒向随机微分方程的解过程对存在并且惟一.

令Mt=¯E[β(T)V(ψ(x0)ζ(T))/Ft],显然μt是¯P-F t鞅,根据鞅表示定理知,存在惟一F t可料适

t应过程

特别地,当t=T时有

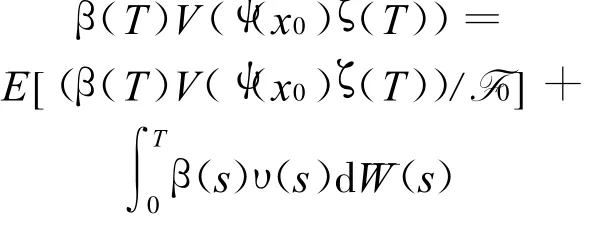
从以上两式可得

若选取

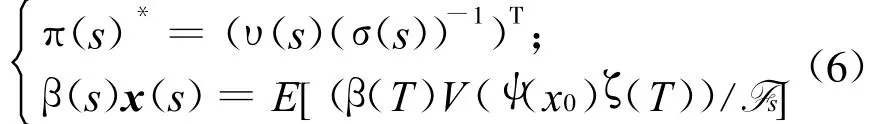
有

倒向随机微分方程(5)存在唯一解过程对

由于x(0)*=¯E[(β(T)V(ψ(x0)ζ(T))]=φ(ψ(x0))=x0,且对应的期末财富为 x(T)*=V(ψ(x0)ζ(T)).因此投资者用初始财富 x0按照策略π(t)*进行投资,期末的财富为 x(T)*=V(ψ(x0)ζ(T)).

证明 2 π(t)*=(υ(t)(σ(t))-1)T是最优化问题(C)的最优投资策略.考虑

如证明1,记其解过程对为

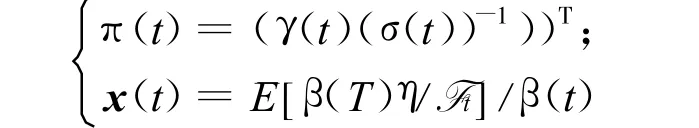
只需证明E[U(x*T)]≤E[U(xT)].由于

在上式两边取期望可得

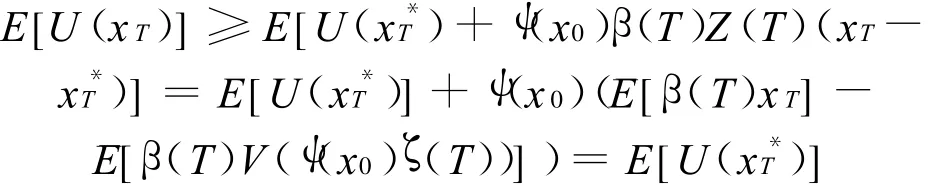
如果用初始财富x0分别按照策略π(t)和 π(t)*投资,有E[U(xT)] ≥E[U(x*T)].因此 π(t)*是最优化问题(C)的最优投资策略.

定理2.3 设投资者的初始财富为 x0,θ＞0,υ(t)1×d是满足M t=M0+∫t0β(s)υ(s)d¯W(s)的F t可料适应过程,其中M t=¯E[(β(T)V(ψ(x0)×ζ(T))/F].若最优组合问题(A)存在最优投资策略 ,则 π(t)*=[υ(t)(σ(t))-1]T,而且

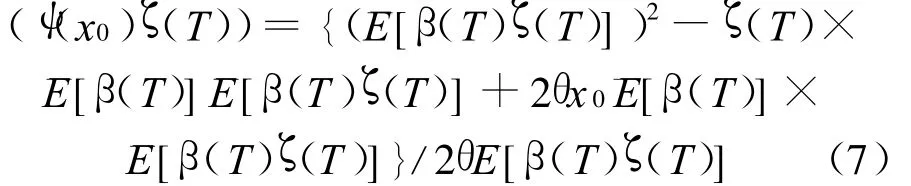
是在此策略下的最终财富.

证明 由定理2.2证明可得

为得到最优化问题(A)的最优投资策略,只需计算 λ=1+2θE(x*T)的值.由上式可得

3 有效前沿

定理3.1 设投资者的初始财富为 x0,θ＞0,υ(t)1×d是满足 Mt=M0+的β(s)υ(s)d¯W(s)的可料适应过程,其中M t=¯E[(β(T)V(ψ(x0)×ζ(T))/].若最优组合问题(A)存在最优投资策略 π(t)*=[(υ(t)(σ(t))-1]T,在最优投资策略下最终财富的有效前沿是如下曲线

证明 当λ取式(8)的表达式时,式(4)便成为式(7).为简化推导,从式(4)有

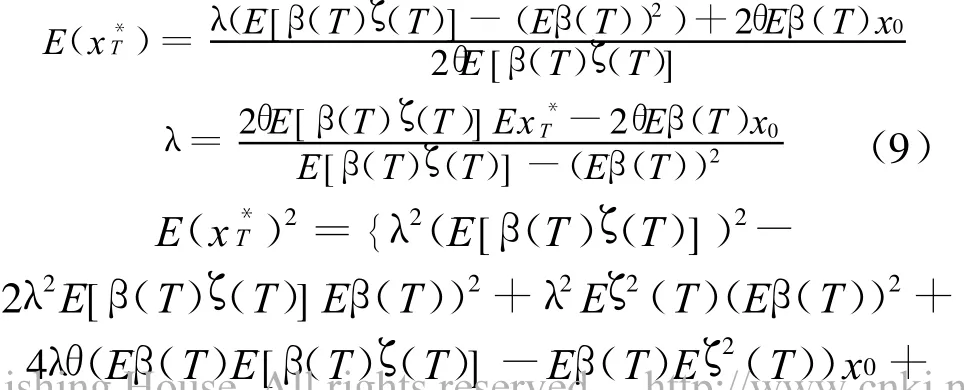
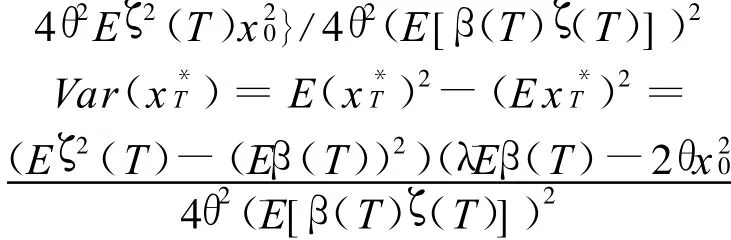
以式(9)代入上式得

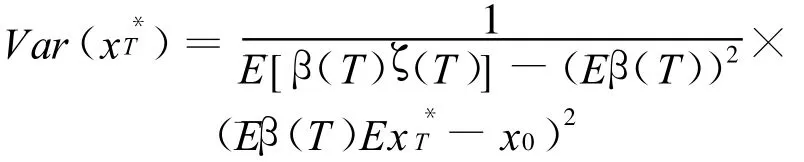
证毕.

根据定理3.1可得如下推论.

推论 如果r(t),b(t),σ(t)是确定性函数(向量、矩阵),均值-方差组合选择问题(A)的有效前沿为如下抛物线

4 结 束 语

自从Markowitz的投资组合理论发表以来,投资组合分析的研究不断向纵深发展.在连续时间框架并且利率假定为随机过程时,本文研究了一般的动态投资组合选择问题.运用倒向随机微分方程的理论与动态最优化方法,得到了连续时间投资组合的有效前沿的解析表达式,有效前沿曲线是一条抛物线,推广了Markowitz的经典结论.

[1] M erton R C.Op timum consump tion and portfo lio ru les in a continuous timemodel[J].JEcon Theory,1971,3:373-413.

[2]Cox J,Huang C F.Op timal consump tion and portfolio polices w hen asset prices follow a diffusion process[J].JEcon Theory,1989,49:33-83.

[3]肖新平.多目标数学规划的最弱有效解[J].武汉理工大学学报:交通科学与工程版,1992,16(1):51-58.

[4]郭子君,吴让泉.具有异常波动市场的消费与投资策略[J].控制理论与应用,2004,21(4):546-549.

[5] Du ffie Darrell,Epstein G.Stochastic differential utility[J].Econometric,1992,60(2):353-394.

[6]Pardoux E,Peng S.A dap ted solution o f a backw ard stochastic differential equation[J].System s and Control Letters,1990,14:55-6.

[7]M a J,Yong J.Forward--backw ard Stochastic Differential Equations[M].New York:Springer-Verlag,1998.

[8]Yong J,Zhou X Y.Stochastic Controls:H am iltonian Systems and HJB Equations[M].New York:Springer-Verlag,1999.