柔性管加筋注浆颗粒流数值模拟
2010-11-29王立中
王立中
(铁道第三勘察设计院集团有限公司,天津 300142)
注浆是岩土工程中一门专业性很强的学术分支,用注浆处理各种岩土工程问题已成为常用的方法。随着注浆技术的日益成熟和发展,它的应用范围和作用逐渐扩大。计算技术的发展,使得采用数值模拟的方式研究均质土体中的注浆成为可能,本文则利用离散元程序PFC2D对现场柔性管加筋注浆试验进行了数值模拟研究。
1 颗粒流的基本假设和理论
1.1 基本假设
颗粒流方法在模拟过程中作了如下假设:
(1)颗粒单元为刚性体。
(2)接触发生在很小的范围内,即点接触。
(3)接触特性为柔性接触,接触处允许有一定的“重叠”量;“重叠”量的大小与接触力有关,与颗粒大小相比,“重叠”量很小。
(4)接触处有特殊的连接强度。
(5)颗粒单元为圆盘形(或球形)。
1.2 基本理论
颗粒流方法在计算循环中,交替应用牛顿第二定律与力—位移定律,其计算过程见图1。
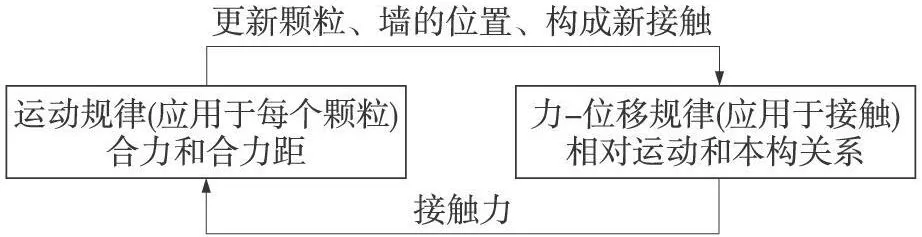
图1 计算过程循环
(1)力-位移定律
通过力-位移定律把相互接触的两部分的力与位移联系起来,颗粒流模型中接触类型有“球-球”接触与“球-墙”接触两种。
接触力Fi可以分解为切向与法向分量

法向分量可以根据下式计算

式中:Kn为接触点法向刚度;Un为接触“重叠”量;ni为接触面单位法向量。
而切向接触力以增量的形式计算

式中:Kn为接触点切向刚度;为计算时步内接触位移增量的切向分量为接触点速度的切向分量;Δt为计算时步。
通过迭加求出切向接触力分量

(2)运动定律
单个颗粒的运动是由作用于其上的合力和合力矩而决定的,可以用颗粒内一点的线速度与颗粒的角速度来描述。运动方程由两组向量方程表示,一组描述了合力与线性运动的关系,另一组是表示合力矩与旋转运动的关系。
线性运动:

旋转运动:

式中:Fi为合力;m为颗粒总质量;g为重力加速度;Mi为合力矩;Hi为角动量。
1.3 颗粒流方法模拟步骤
由于篇幅所限,此处仅对采用颗粒流方法进行数值模拟的步骤简述如下:
(1)根据模拟示意图定义模型的详细程度,定义模拟对象。
(2)分析模拟对象在一定初始条件下的特性,建立力学模型的基本概念。
(3)在建立实际工程模型之前,先构造并运行一系列简化的测试模型。
(4)根据实际情况补充模拟问题的数据资料。
(5)模拟运行的进一步准备。
(6)运行计算模型。
(7)解释结果。
2 PFC2D数值模拟方案及模型建立
2.1 土体中注浆模拟实验方案
土体注浆模拟采用单孔注浆的形式,设定一级围压(围压为100kPa),注浆压力由低到高依次递增。研究内容主要为:在一定围压条件下,浆液扩散半径与注浆压力的规律。
2.2 计算参数的选择
所选择的模拟对象为长沙至重庆公路通道高速公路泸溪沅水大桥附近土体,其主要物理力学参数见表1。

表1 试验土体的基本物理力学指标
颗粒粒径:为了更好地逼近原地基土在微观上的各向异性和不均匀性,在生成二维颗粒流PFC2D仿真模型试样时设定颗粒试样是由不同半径的颗粒单元所组成,颗粒半径R的分布采用从Rmin到Rmax的均匀分布,数值模拟计算参数见表2。

表2 PFC2D数值试样的基本输入参数
3 PFC2D数值模拟100kPa条件下浆液的扩散半径
预先为颗粒集模型施加100kPa侧向压力,注浆压力由100kPa依次增大,模拟实验结果如图2所示,图中蓝色颗粒为裂隙,红色圆为测量圆,其半径分别为0.35m,0.7m,1.05m,1.4m,1.75m。
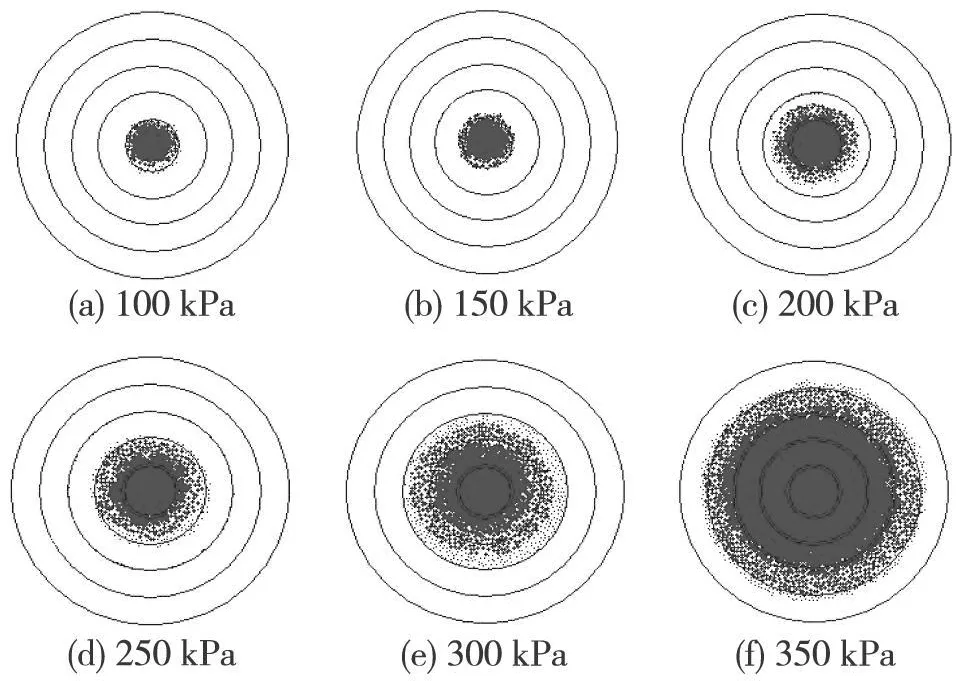
图2 围压为100kPa时的不同注浆压力浆液扩散半径
根据测量圆半径,从以上实验结果中很容易得出不同注浆压力时浆液的扩散半径,具体数值模拟结果见表3。

表3 注浆压力与注浆半径对应关系
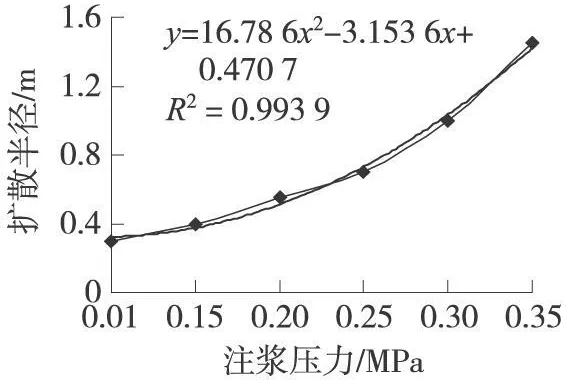
图3 注浆压力与扩散半径拟合
图3中虚线为围压100kPa时,注浆压力与浆液扩散半径散点图,黑线为注浆压力与浆液扩散半径的趋势线图。从趋势图可见,在注浆压力较低时,浆液扩散半径与注浆压力的比值(斜率)小,随着注浆压力的增大,斜率也逐渐变大,这表明增加等量注浆压力的情况下,浆液扩散半径的增量变大。这表明增加等量注浆压力的情况下,浆液扩散半径的增量变大。当注浆压力增大到一定值以后,土体结构破坏,土壤中较小裂隙互相贯通,形成较大的裂隙,土体稳定结构被破坏,即使很小的压力增量,也会使裂隙扩展范围增加很多。
比较可知,现场单点注浆平均压力0.36MPa时,浆液扩散半径最大为1.1m,最小为0.7m,综合平均扩散半径为0.88m,实际注浆扩散半径比注浆压力350kPa时数值模拟最大扩散半径比小0.35m,与注浆压力300kPa时扩散半径相差不大,仅为0.1m。
PFC2D数值模拟注浆半径与实际注浆结果比较可知,现场注浆浆液扩散半径要达到达到1.2m,注浆压力必须在350kPa以上。从现场注浆试验[1]可知,实际注浆压力应该大于0.4MPa,才能保证现场注浆所达到的扩散半径。
4 结论与建议
(1)通过数值模拟的结果与实际注浆扩散半径比较得出:在相同注浆压力下,两者的扩散半径值在一定程度上达到了相符,但还是存在一定的误差,最大的误差为0.35m。
(2)通过对实际注浆半径与数值模拟注浆半径存在误差进行分析,得出其影响因素包括:数值模拟过程中没考虑实际注浆中的土体重力对注浆半径的影响及土体受到的不均匀压力的影响。
(3)在用离散元软件PFC2D模拟柔性管加筋注浆扩散半径时,没有考虑土体的自重及不等向压力,而考虑的是等值围压,这对模拟结果会产生多大的影响,还有待进一步研究。
[1]王立中.柔性管加筋注浆新技术试验及应用研究[D].长沙:中南大学,2008
[2]曾 远.土体破坏细观机理及颗粒流数值模拟[D].上海:同济大学,2006
