非线性破坏准则下浅埋隧道围岩压力的极限分析

杨小礼，王作伟

(中南大学 土木建筑学院，湖南 长沙，410075)

围岩是指隧道开挖后其周围产生应力重新分布的岩土体，或指隧道开挖后对其稳定性能产生影响的土体[1]。隧道开挖后，因围岩变形、松弛等，作用于隧道支护或衬砌结构上的压力称为围岩压力。对于浅埋隧道，围岩压力的计算方法主要有土柱理论、泰沙基极限平衡法及铁路、公路隧道设计规范所推荐的方法[1−2]，这些方法都是根据极限平衡理论求解。随着极限分析理论在土压力、边坡稳定以及地基承载力等岩土工程领域中的不断发展[3−6]，国内外一些学者将极限分析理论应用于隧道围岩稳定性分析，如：Atkinson等[7]利用极限分析上、下限定理和模型试验方法分析了无黏性土浅埋隧道稳定性问题；Davis等[8]根据上限定理，假定了4种不同的破坏模式，对黏性土在不排水条件下的浅埋隧道围岩稳定性进行了分析；Leca等[9]利用上、下限定理，研究了浅埋隧道工作面的三维稳定性问题；姜功良[10]应用极限分析有限元方法求解隧道的稳定系数，改善了上限分析结果。以上浅埋隧道稳定性研究是基于土体线性破坏准则。然而，研究表明[11−14]：多数土体服从非线性破坏准则，线性破坏准则只是其中一个特殊情况。非线性破坏准则在岩土工程中已经得到广泛应用[15−17]。在土体非线性破坏准则下，本文作者运用极限分析上限定理，根据泰沙基破坏模式，计算浅埋隧道围岩压力的上限解。

1 基本原理

1.1 非线性破坏准则

根据文献[17]，土体非线性破坏准则可表达为：

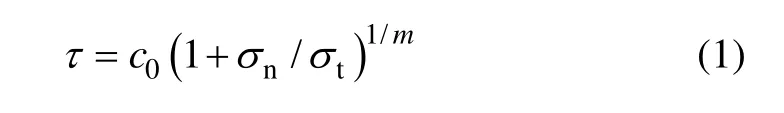
其中：σn和 τ分别为破坏面上的正应力和剪应力；c0为初始黏聚力；σt为轴向拉应力；m为非线性系数。c0，σt及m可以由实验得到。当m=1时，式(1)变为线性Mohr-Coulomb破坏准则的表达式。非线性破坏准则式(1)的切线方程为：

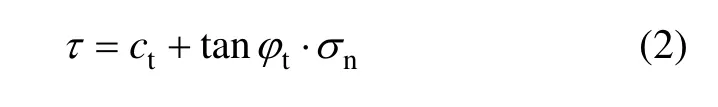
其中：ct和tan φt分别表示切线的斜率和截距。联立式(1)和(2)得ct的表达式为：

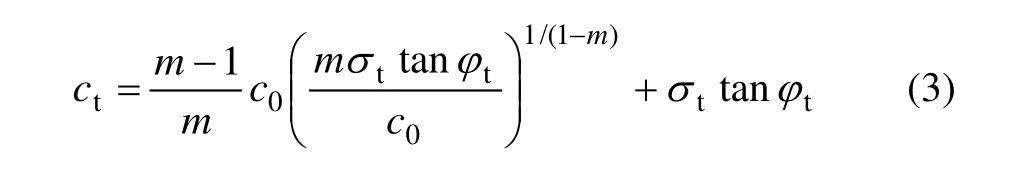
根据切线法原理[15]可知，由式(2)和(3)求出的上限解必定是非线性关系式(1)的上限解。

1.2 极限分析上限定理

极限分析法建立在虚功率原理基础上。虚功率原理表明：对于理想的土体，任意一组静力容许的应力场和任意一组机动容许位移速度场，外力的虚功率等于物体所能接受的虚变形功率。在虚功率原理的基础上可推导出上限定理为：在所有的机动容许的塑性变形速度场相对应的荷载中，极限荷载最小[3]。

2 破坏模式与速度场

泰沙基理论[18]是基于极限平衡法计算隧道围岩压力的，其破坏模式如图1所示。本文将其应用到极限分析法中，假定隧道顶板与边墙的支护反力均分布均匀。顶板以上矩形块ABB1A1的移动速度为v0，方向竖直向下；边墙处三角形块移动速度为v1，其相对速度为v01。根据相关联流动法则，刚性块之间速度间断线上的速度矢量方向与间断线夹角为φt，且各速度矢量满足矢量闭合条件，从而得到破坏模式对应的速度场，如图2所示。

图1 极限平衡破坏模式Fig.1 Limit equilibrium failure mechanism

图2 与破坏模式相对应的相容速度场Fig.2 Velocity hodograph corresponding to above failure mechanism

3 围岩压力计算

3.1 速度关系

根据刚性块应满足运动许可条件及图2，可得v0，v1和v01之间的关系如下：

3.2 外力功率

3.2.1 重力功率

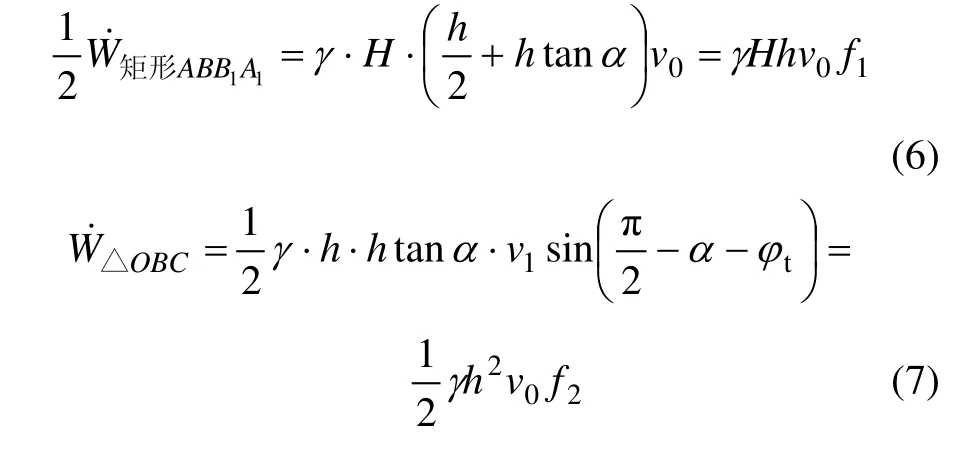
所以，

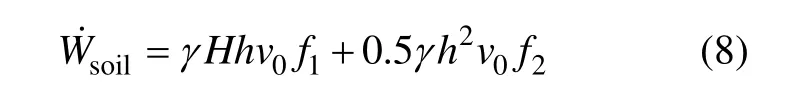
3.2.2 支护反力功率

隧道顶板竖向支护反力q和边墙水平支护反力e所做功率之和W˙T为：

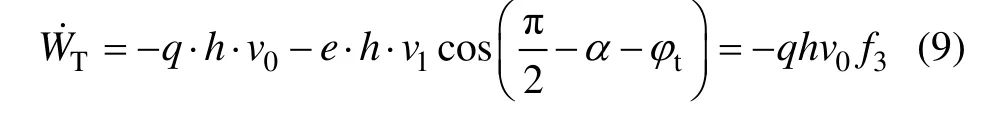
其中：e=Kq；K为待定参数。

3.3 内部能量耗散率

内能耗散的一半W˙int等于速度间断线 OB和 BC上的能量耗散之和，计算式如下：

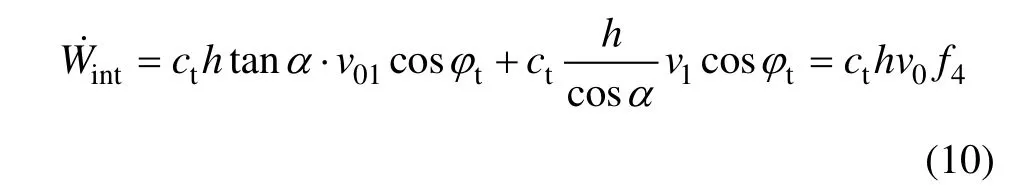
3.4 围岩压力q

根据虚功率原理，外力做功与内部耗散能量相等，得竖向支护反力q的表达式：

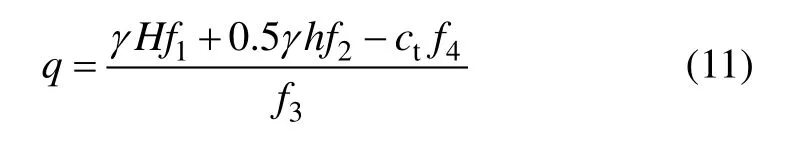
其中，f1～f4是关于α和tϕ的无量纲函数，其表达式为：

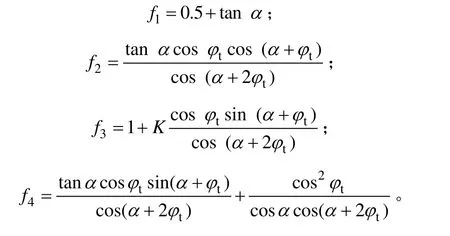
4 数值计算与分析

4.1 上限解的优化

由式(11)可知，当其他参数一定时，由1组角度α和tϕ可以完全确定其破坏形状，同时对应1个上限解。于是，问题转化为：在满足物理意义的约束条件下，寻求目标函数 q = f (α,ϕt)的最大值。由图2可知破坏模式对应的约束条件为：

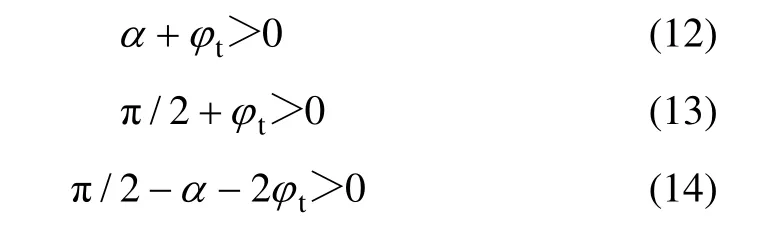
在约束条件(12)～(14)下，不断调整α和tϕ，然后，代入式(11)，得出最大q，即为优化上限解。此过程可以运用序列二次规划算法，通过 Matlab软件编程来实现。

4.2 对比分析

对于浅埋隧道，可据泰沙基理论确定围岩压力[18]：

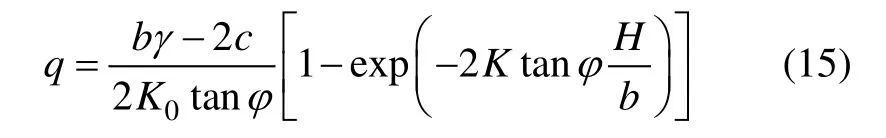
其中：K0为隧道上方岩土层侧压力系数，泰沙基[18]根据实验结果建议K0取1.0～1.5；b为地表面到拱顶的滑动地块的宽度，

取隧道埋深H=20 m，隧道跨度h=10 m，围岩容重 γ=20 kN/m3，内摩擦角 φ=18˚，黏聚力 c=10.0 kPa。根据式(15)～(16)可以计算围岩压力q，结果见表1。在线性破坏准则下，即当 m=1.0时，取 K=0.40～0.65，按本文极限分析方法计算得出围岩压力q，如表1所示，其中：q0为用泰沙基极限平衡法所得的围岩压力。

表1 泰沙基法与本文方法计算结果比较Table 1 Comparisons of calculation results between limit equilibrium solutions and present solutions

从表1可看出，采用本文方法所得结果与采用泰沙基法所得结果比较接近，说明本文极限分析方法是可行的。

4.3 非线性破坏准则的影响

取隧道埋深H=20 m，隧道跨度h=10 m，围岩容重 γ=20 kN/m3，黏聚力 c=10.0 kPa，拉应力 σt=30 kPa。在非线性破坏准则下，取 m=1.1～1.4，计算泰沙基破坏模式下的围岩压力上限解，结果如表2所示。

表2 非线性破坏准则下的围岩压力及破裂角Table 2 Results of break angles and earth pressures using different nonlinear factors

由表2可以看出：当K一定时，随着非线性系数m的增大，围岩压力q和破裂角α均有增大的趋势。因此，在土体服从非线性破坏准则时，如何准确地确定非线性系数对于围岩压力的计算有重要作用。当K=0.8，m取1.1～1.4时，绘制出经过优化的破坏模式，如图3所示。

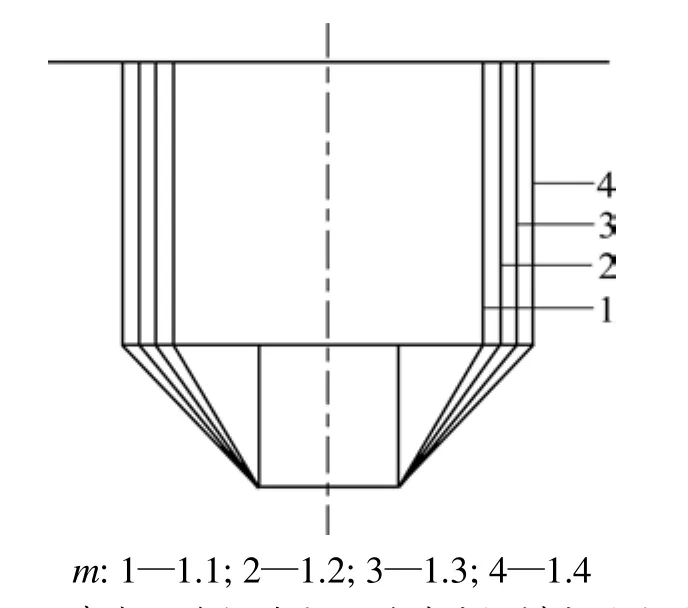
图3 非线性系数对浅埋隧道破坏模式的影响Fig.3 Influence of nonlinear factor on failure mechanism by optimization

5 结论

(1) 根据极限分析方法中的上限定理计算浅埋隧道围岩压力时，泰沙基破坏模式是适用的。

(2) 在非线性破坏准则下，根据极限分析上限定理，推导出浅埋隧道围岩压力的计算公式，并计算出围岩压力的最优解。

(3) 非线性系数m对围岩压力的上限解有明显的影响。随着m的增加，围岩压力呈非线性增大趋势。

[1]TB 10003—2001, 铁路隧道设计规范[S].TB 10003—2001, Code for design of railway tunnel[S].

[2]JTG D70—2004, 公路隧道设计规范[S].JTG D70—2004, Code for design of road tunnel[S].

[3]Chen W F. Limit analysis and soil mechanics[M]. New York:Elsevier Scientific Publishing Company, 1975.

[4]Soubra A H, Regenass P. Three-dimensional passive earth pressures by kinematical approach[J]. Journal of Geotechanical and Geoenvironmental Engineering, 2001, 126(11): 969−978.

[5]Donald I, Chen Z Y. Slope stability analysis by the upper bound approach: fundamentals and methods[J]. Canadian Geotechnical Journal, 1997, 34(6): 853−851.

[6]Wang Y J, Yin J H, Chen Z Y. Calculation of bearing capacity of a strip footing using an upper bound method[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2001, 25(8): 841−851.

[7]Atkinson J H, Potts D M. Stability of shallow tunnel in cohesionless soil[J]. Geotechnique, 1977, 27(2): 203−215.

[8]Davis E H, Gunn M J, Mair R J. The stability of shallow tunnel and underground openings in cohesive material[J]. Geotechnique,1980, 30(4): 397−416.

[9]Leca E, Dormieux L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J].Geotechnique, 1990, 40(4): 581−606.

[10]姜功良. 浅埋软土隧道稳定性极限分析[J]. 土木工程学报,1998, 31(5): 65−72.JIANG Gong-liang. Limit analysis of the stability of shallow tunnels in soft ground[J]. China Civil Engineering Journal, 1998,31(5): 65−72.

[11]Lade P V. Elasto-plastic stress-strain theory for cohesionless soil with curved yield surface[J]. International Journal of Solids Structure, 1977, 13: 1019−1035.

[12]Hoek E, Brown E. Empirical strength criterion for rock masses[J]. Journal of Geotechnical Engineering Division, 1980,106(9): 1013−1035.

[13]Agar J G, Morgenstern N R, Scott J. Shear strength and stress-strain behavior of Athabasca oil sand at elevated temperatures and pressure[J]. Canadian Geotechnical Journal,1985, 24(1): 1−10.

[14]Santarelli F. Theoretical and experimental investigation of the stability of the axisymmetric borehole[D]. London: University of London, 1987.

[15]YANG Xiao-Li, YIN Jian-Hua. Estimation of seismic passive earth pressures with nonlinear failure criterion[J]. Engineering Structures, 2006, 28(3): 342−348.

[16]YANG Xiao-Li. Upper bound limit analysis of active earth pressure with different fracture surface and nonlinear yield criterion[J]. Theoretical and Applied Fracture Mechanics, 2007,47(1): 46−56.

[17]Zhang X J, Chen W F. Stability analysis of slopes with general nonlinear failure criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(1): 33−50.

[18]樗木武. 隧道力学[M]. 关宝树, 麦倜曾, 译. 北京: 中国铁道出版社, 1983.CHU Mu-wu. Tunnel mechanics[M]. GUAN Bao-shu, MAI Ti-zeng, trans. Beijing: China Railway Press, 1983.