多轴半挂车转向传动机构优化

方志刚，过学迅，王力波

（1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北武汉430070；2.湖北三江航天万山特种车辆有限公司，湖北孝感432100）

随着国内重型汽车的飞速发展，多轴半挂车逐渐成为主流，但是我国的专用汽车产业还很不成熟，与发达国家相比，生产规模小，生产工艺低，技术水平不高。德国的GOLDHOFER公司、法国的NICOLAS公司等世界顶级企业对半挂车进行了大量的研究，处于世界领先地位。现以某型号半挂车为对象，针对其转向时车轮易侧滑、轮胎易磨损的问题，对其转向传动机构进行研究分析，以实现转向轮最大转向角达到45°，所有转向车轮能实现纯滚动的目标。通过初步设计选型和计算，得到该半挂车的基本参数和转向参数，然后运用科学计算软件MATLAB对该半挂车的转向传动机构进行优化处理。

1 结 构

图1 该半挂车转向系

图2 转向梯形

该优化的车型为4轴半挂车。其中，第4轴为支撑轴，其余均为转向轴，且第1轴为驱动轴，如图1所示，图1中从右到左依次为第1～4轴。该多轴半挂车的转向梯形为断开式，如图2所示，且其转向梯形非空间梯形，它所在的平面平行于水平面即为平面梯形。该半挂车转向梯形的转向机构为2个并列对称的联动双摇杆机构，其通过中间共用的转向板绕A点转动时带动双摇杆机构ABCD和AEFG实现左右转动，从而带动与其连接车轮转向来实现整车的转向功能。在直线行驶状况下，双摇杆机构中的A点位置固定，D点到A点在汽车坐标系的Y方向位置固定，CD即臂长为常量，D点在汽车坐标系的X方向的坐标以及B点的坐标均为变量。对于转向梯形ABCD与AEFG，当转向板绕A点沿顺时针转动角度θ时，右侧车轮因转向板转动而绕G点也绕顺时针方向转动，转向角为β，且此时右侧为整车转向时的外侧。左侧车轮绕D点也沿顺时针方向转动，转向角为α，且左侧为整车转向时的内侧。

2 原 理

2.1 优化原理

对汽车转向传动机构优化的目的是使所有转向轮在转向时尽量接近理想转角。因此，首先以第1轴内侧转向轮最大转角达到45°，所有转向车轮能实现纯滚动为目标，根据该4轴半挂车的结构，计算出各个车轮的理想转角。计算原理见图3，第1轴的内侧转向轮的中心线与第4轴车轮的中心线的交点形成一个转向中心，理想状况下，其他所有转向轮的中心线都应该汇集于该转向中心，这样所有车轮均做纯滚动。又因该半挂车各轴距离相等，根据轴距与轮距、由式（1）与式（2）即可计算出各个转向轮的理想转角。其中需要用到的整车参数有轴距r、轮距s以及第1轴内侧转向轮最大转角。另外，k为转向中心到第4轴内侧轮的距离，αi为第i轴外侧轮理想转角，βi为第i轴内侧轮理想转角，i＝1、2、3，θ为转向板转角。

图3 转向优化原理

半挂车在转向时，其实际转角受转向梯形约束而不能与理想转角完全相等。图4为转向梯形转动图，以A点为原点，GF的所指方向为Y轴正方向，在AEFG所在平面用右手定则可得X轴的正方向如图4所示。转向梯形的初始位置为AEFG，转向板转动θ后转向梯形的位置为AE1F1G，对应的车轮转角为β。假设E点坐标为（XE，YE），G点坐标为（z，s/2），其中臂长 FG为定值m，则 F点坐标为（r/2，z+m）。根据平面几何基础知识，由梯形中4点坐标很容易求出各个角的角度值，在设定了各点坐标后梯形各边长均不变，因此当EA绕A点转到E1A转动θ度时，也很容易求出β关于θ的解。

然后将求得的实际转角与理想转角相比较，做出合适的目标函数。最后求解目标函数的最小值及最小值对应的转向梯形结构，则该转向梯形决定的实际转角与理想转角最为接近，即所有转向轮侧滑与磨损达到最小。

2.2 目标函数

评价优化好坏的目标函数采用最小二乘法得出，并引入加权因子。这是因为在最常使用的中间位置附近小转角范围内，偏差应该尽可能的小，以减少速度较高时轮胎的磨损。而在不常使用的较大转角的角度范围，可适当放宽要求。如式（3），其中βt和βr代表内侧理想转角与内侧实际转角，αt和αr代表外侧理想转角与外侧实际转角。λ代表转向板转角，ω（θ）代表权重，与θ有关。

其中，该半挂车有3个转向板，转向板之间由拉杆连接传递动力，由于转向板的拉杆定位孔位置相对于转向板转动中心位置固定，使各转向板在转动时转角均相等。该半挂车的最大转角为45°，即在转向时第1轴的内侧轮最大转角可达45°，半挂车最大转角为45°的约束条件仅与第1轴直接关联，与其他转向轴则由转向板通过拉杆传递动力来关联，这样的约束对直接求解其他转向轴转角比较困难。因此可找出转向板与第1轴转向轮的关系，将最大转角为45°的约束条件转化为转向板的转角约束条件，用转向板的转角来描述各轴转向轮的转角大小，这样就可以实现用统一的转向板转角来约束所有的转向轴转角。

通过求解第1轴转向轮与转向板的转向梯形的关系可知道，在内侧轮转角达到45°时，转向板转角为43.739°，而转向板达到44°时，内侧轮转角达到了45.31°。在计算目标函数时取1°的间隔来求解实际转角与理想转角的偏差，因此取λ的最大值为44°，即n为44。当λ值为0时，所有车轮的转角均为零，该半挂车为直线行驶状态，不存在转向的问题，因此不用考虑。

在目标函数中，根据转向板从1～44°的转角可计算出44组理想转角。对每度的理想转角与实际转角的差值平方赋予权重，再进行累加就得到了目标函数值。权重由车辆在行驶过程中转向板转角λ的出现频率来确定，在本次优化中权重如式（4）所示。

2.3 约束条件

考虑到该半挂车的实际情况，把本优化的约束分为3个部分。

第1部分：根据半挂车的实际尺寸如轴距、轮距、前一转向梯形的定位等，对各轴转向梯形的x、y、z数值选取范围进行约束，以保证转向梯形不会与车桥、车架发生干涉以及转向梯形之间不会发生干涉。

第2部分：对转向梯形的运动进行约束，使转向板在达到最大转角时车轮也不会反转。

第3部分：对转向梯形的传动角进行约束，使最小传动角不会小于30°，保证良好的受力状况。

3 转向优化程序

转向优化程序流程图如图5所示。

根据优化原理，目标函数以及相应的约束编写适当的程序，编写原则是使问题在能得到可靠的收敛解的同时，程序尽量简单易改。

图5 转向优化程序流程图

4 优化结果

由程序计算得原始转向机构各轴的目标函数值和优化之后的各轴转向机构的目标函数值，如表1所示。

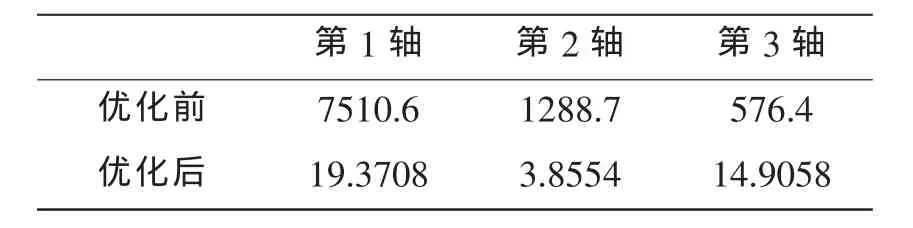
表1 各轴转向机构目标函数值的比较

各转向轴的理想转角与实际转角对照图及原始数据与优化后数据的对照图如图6。

可以看到，优化后的车轮转角明显比原始结构的车轮转角要贴近理想转角。第1～2根轴的优化效果最好，实际转角与理想转角十分吻合。第3轴的优化效果相对要差一些，这是靠近转向中心线、理想转角偏小的缘故，这种趋势与实际试验的结果是一致的。

图6 各转向轴优化前后的数据与理想数据的对照图

5 结 论

运用MATLAB优化工具箱对某型号半挂车转向传动机构进行了优化。在目标函数的求解时通过将最大转向角的约束条件转化为转向板的转角约束条件，使得各个转向轴的目标函数得到统一；并对转向梯形的参数进行约束，在保证良好地动力传递的情况下，车轮不会反转，其他部分不会发生干涉；并且分析比较了优化前后的目标函数值，将它们与理想转角对比，证明了优化方法的可行性与正确性。本研究方法改善了半挂车常见的轮胎易磨损与车轮易侧滑的现象，增加了多轴半挂车的转向稳定性，同时也可以为今后多轴半挂车转向机构的优化提供参考。

[1]郭朋彦，石博强，肖成勇，等.多轴线液压挂车转向机构优化设计[J].工程机械，2008（10）：32-37.

[2]李玉民，过学迅，王文家.整体式转向梯形的运动分析与优化设计[J].拖拉机与农用运输车，2001（2）：18-22.

[3]濮良贵，纪名刚.机械设计[M].8版.北京：高等教育出版社，2006.

[4]张志涌，杨祖樱.MATLAB教程[M].北京：北京航空航天大学出版社，2006.

[5]王望予.汽车设计[M].4版.北京：机械工业出版社，2004.