某些图的线性荫度问题
2010-11-27王雪梅
王雪梅
(河南工程学院 数理科学系, 河南 郑州 451191)
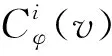
1 引 理
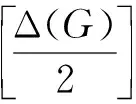
下面是两个本文将用到的引理.
引理1[2-8]若一个连通图G满足Δ=1,2,3,4,5,6,8,则LAC成立.

2 主要结果
下面给出本文所给的结果.
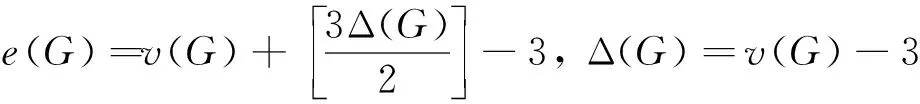
(1)存在一个点u, 使得d(u)=7;
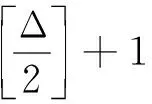
(3)任意两个最大度点都不相邻.
则有以下两种情况:
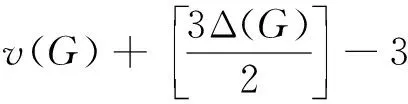
(2)若G是第二类的图,则必是最小的第二类图,且有以下两个结论成立:
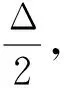
②若G有度数为1的顶点v0, 则它只有唯一的最大度点.这个最大度点就是与v0相邻的顶点.
证明(1) 若v′不是最大度点,则令G′=G-u′v′, 有e(G′)=e(G)-1,v(G′)=v(G),

Δ+1, 所以dG′(u′)+dG(v′)≤Δ-2,
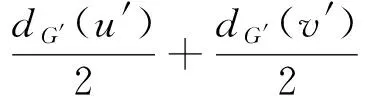
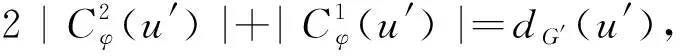
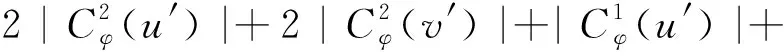

dG′(u′)+dG′(v′).
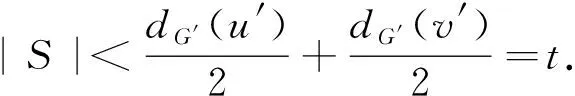
与原假设矛盾, 所以结论1成立.
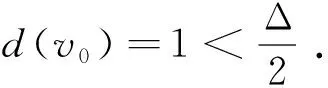
从而由结论1知,v0的邻点v1必为最大度点.
下面证明最大度点的唯一性.
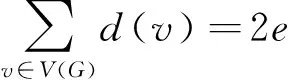

t≤2. 这就是说t=2.
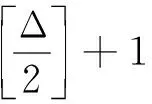
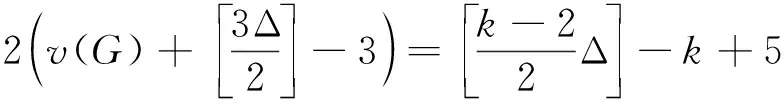
与原假设矛盾.
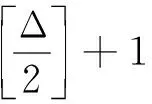
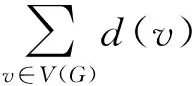
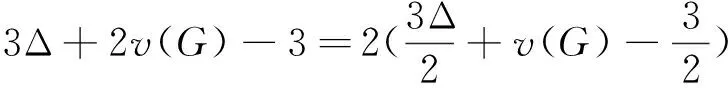
与原假设矛盾.
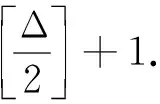
以上矛盾说明:G只有一个最大度点.
证毕.
3 结 论
图论中有关染色的研究成果已经相对完善,对网络方面和运输问题的作用也日趋明显[9-15].但是染色理论分支的荫度问题还有一些尚待解决,本文找出了第一类图和第二类图的一个必要条件,但是它的充分条件问题还有待解决.
参考文献:
[1] 邦迪·J·A,默蒂·U·S·R.图论及其应用[M].北京:科学出版社,1984.
[2] 吴建良.边数较少的图的线性荫度.山东大学学报:理学版,2005,40 (3):11-14.
[3] 吴建良.Halin图的一些路分解[J].山东矿业学院学报:自然科学版,1996(15):219-222.
[4] WU J L. The linear arboricity of Series-Parallel graphs[J]. Graphs and Comb,2000(16):367-372.
[5] WU J L. On the linear arboricity of planar graphs[J]. J Graph Theory, 1999(31):129-134.
[6] ALON N. The linear arboricity of graphs[J]. Mathematics, 1988(62): 311-325.
[7] ENOMOTO H, PEROCHE B.The linear arboricity of some regular graphs[J]. J Graph Theory,1984(8):309-324.
[8] GULDAN F. Some results on linear arboricity[J]. Graph Theory, 10 (1986): 505-509.
[9] HABIB M P.Some problems about linear arboricity[J].Discrete Math,1982,41(2):219-220.
[10]BERMOND J C,FOUQUET J L, HABIB M,et a1.On linear k-arboricity[J]. Discrete Math,1984,52(2/3):123-132.
[11]FU H G, HUANG G Q. The linear 2-arboricity of complete bipartite graphs[J].Ars Combin,1994,38(3):309-318.
[12]THOMASSEN C. Two-coloring the edges of a cubic graph such that each monochromatic component is a path of length at most 5[J]. J Combin Theory Ser B,1999,75(1):100-109.
[13]ZHANG Z H. Algorithmic aspects of linear k-arboricity[J].Taiwanese J Math,1999,3(1):73-81.
[14]ZHANG Z H. CHEN B L, FU H L, et a1. Linear k-arboricities on trees[J].Discrete Appl Math, 2000,103 (1/3):281-287.
[15]AKIYAMA J.Three developing topics in graph theory[D]. Tokyo: University of Tokyo,1980.
