基于核和灰度的区间灰数代数系统
2010-11-27刘卫锋张又林许宏伟
刘卫锋,何 霞,张又林,许宏伟
(郑州航空工业管理学院 数理系,河南 郑州 450015)
刘思峰教授等在文献[1-3]中提出的灰数的核和灰度的概念,在一定程度上解决了灰数运算存在的难题,特别是较为完善地解决了区间灰数运算的问题.但是,关于灰数代数系统中运算的性质与系统本身结构问题,一直是灰色系统理论研究的一个难题,至今仍无令人满意的结果,这不仅在一定程度上阻碍着灰色系统理论的应用,而且影响着灰色系统理论的发展以及学科自身的完整性与优美性.
本文在区间灰数的核和灰度的基础上,从代数学的角度对区间灰数的代数结构进行了讨论,并给出了一系列结论,从而进一步完善了区间灰数运算和区间灰数代数系统.
1 核和灰度
1.1 核和灰度的概念
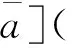
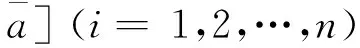
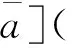
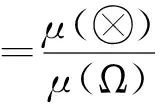

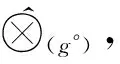
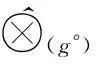
1.2 基于核和灰度的区间灰数运算法则[1]
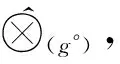
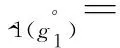
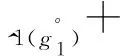
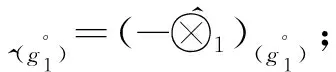
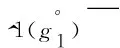
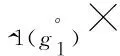
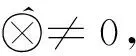
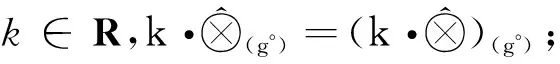
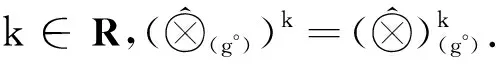
2 基于核和灰度的区间灰数的算术运算
2.1 基于核和灰度的区间灰数的加法运算
(1)加法满足交换律和结合律;
(2) 0是单位元;
(4)加法消去律不成立;例如,30.3°+10.2°=30.3°+10.1°,而10.2°≠10.1°.
(5)
因为对于R(⊗)上的运算+来说,不仅运算封闭,而且满足结合律和交换律,故
(6)
显然, 0是单位元,故再有(5)知,
2.2 基于核和灰度的区间灰数的乘法运算
(1)乘法满足交换律和结合律;
(2) 1是单位元;
(4)乘法消去律不成立;例如, 30.3°×10.2°=30.3°×10.1°,而10.2°≠10.1°;
(5)
(6)
3 基于核的区间灰数的逆元
区间灰数的简化形式为区间灰数的相关运算带来了极大的方便,但是,基于核和灰度即简化形式的区间灰数在不同运算下,其逆元又该如何定义呢?基于此,我们从核的角度分别为具有加法和乘法的区间灰数代数系统定义了逆元,并在此基础上探讨区间灰数代数系统的性质.
3.1 基于核的区间灰数加法的逆元
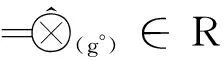
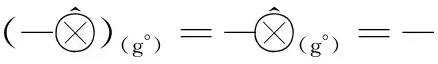
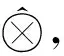
根据该定义,有
因此,这与文献[4-5]中关于灰数的自差运算结果是一致的.
命题1 在基于核的逆元的意义下,
证明首先,由法则1知,加法运算是封闭的;其次,由2.1内容知,加法是可交换和可结合的,且存在单位元0; 最后,由定义6知,每个区间灰数存在唯一个逆元.即有
命题2 已知区间灰数集合R(⊗),令关系
r={<⊗1,⊗2>|⊗1,⊗2∈R(⊗)
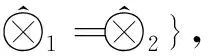
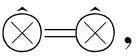
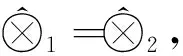

由以上性质可知, r是R(⊗)上的等价关系.
定义7 令 r 是R(⊗)上的等价关系,对于任意⊗1∈R(⊗),集合
[⊗1]={⊗|⊗∈R(⊗),<⊗,⊗1>∈r}
称为元素⊗1形成的等价类.
命题3 设[⊗1]={⊗|⊗∈R(⊗),
<⊗,⊗1>∈r},[⊗2]={⊗|⊗∈R(⊗),
<⊗,⊗2>∈r},则[⊗1]∩[⊗2]=Φ
或者[⊗1]=[⊗2]=Φ.(证明略)
定义8 令r是R(⊗)上的等价关系,其等价类的集合{[⊗1]|⊗1∈R(⊗)}称为R(⊗)关于r的商集,记作R(⊗)/r.
命题4 商集R(⊗)/r构成商群.
证明任意[⊗1],[⊗2]∈R(⊗)/r, 定义一个加法:[⊗1]+[⊗2]=[⊗],其中,
显然,在基于核的逆元的意义下,我们规定的加法满足群的所有条件,故商集R(⊗)/r是商群.
3.2 基于核的区间灰数关于乘法的逆元
类似于基于核的区间灰数关于加法的逆元,我们有基于核的区间灰数关于乘法逆元的定义和结论.
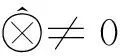
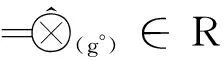
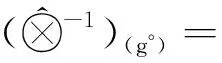
命题5 在基于核的逆元的意义下,
命题6 已知区间灰数集合R(⊗)*,令关系
r={<⊗1,⊗2>|⊗1,⊗2∈R(⊗)*

定义9 令r是R(⊗)*上的等价关系,对于任意⊗1∈R(⊗)*,集合
[⊗1]={⊗|⊗∈R(⊗)*,<⊗,⊗1>∈r}称为元素⊗1形成的等价类.
命题7 设[⊗1]={⊗|⊗∈R(⊗)*,
<⊗,⊗1>∈r},[⊗2]={⊗|⊗∈R(⊗)*,<⊗,⊗2>∈r},
则[⊗1]∩[⊗2]=Φ或者[⊗1]=[⊗2].(证明略)
定义10 令r是R(⊗)*上的等价关系,其等价类的集合{[⊗1]|⊗1∈R(⊗)*}称为R(⊗)*关于r的商集,记作R(⊗)*/r.
命题8 商集R(⊗)*/r构成商群. (证明略)
4 基于核和灰度的区间灰数分类
下面以核和灰度为基础,从距离的角度来考虑区间灰数的分类问题.
命题9 已知区间灰数集合R(⊗),令关系
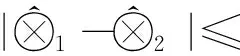
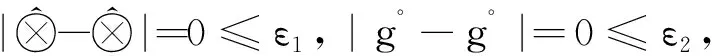
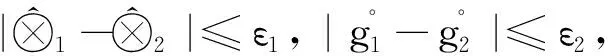
由以上性质可知, r是R(⊗)上的相容关系.
定义11 令r是R(⊗)上的相容关系,对于任意⊗1∈R(⊗),集合
[⊗1]={⊗|⊗∈R(⊗),<⊗,⊗1>∈r}
称为元素⊗1形成的相容类.
命题10 令r是R(⊗)上的相容关系,其相容类的集合{[⊗1]|⊗1∈R(⊗)}构成R(⊗)的一个覆盖. (证明略)
5 结 论
本文通过区间灰数的核和灰度的概念,利用区间灰数的简化形式,分别探讨了区间灰数代数系统关于加法和乘法所具有的性质.然后,利用区间灰数的核为区间灰数定义了逆元,在此基础上,先后探讨了基于核的逆元下的区间灰数代数系统的性质,得出了一系列的结论,从而完善了区间灰数代数系统.最后,从距离的角度建立了区间灰数相容类.这些探讨有助于人们掌握区间灰数代数系统的性质和结构,对于进一步研究灰数代数系统具有一定的理论意义.
参考文献:
[1] 刘思峰,方志耕,谢乃明.基于核和灰度的区间灰数运算法则[J].系统工程与电子技术,2010, 32(2) :313-316.
[2] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].5版.北京:科学出版社,2010.
[3] 刘思峰,林益.灰数灰度的一种公理化定义[J].中国工程科学,2004,6(8):91-94.
[4] 邓聚龙.灰色控制系统[M].2版.武汉:华中理工大学出版社,1993.
[5] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[6] 左孝凌,李为鑑,刘永才.离散数学[M].上海:上海科学技术文献出版社,1982.
