网上考试系统中组卷策略的实现
2010-11-27张顺利冯广丽任鹏飞
张顺利,冯广丽,任鹏飞
(1. 河南工程学院 计算机科学与工程系,河南 郑州 451191;2. 河南工程学院 电气信息工程系,河南 郑州 451191)
组卷是指从庞大的试题库中按照给定的要求抽选试题组成试卷的过程,组出的试卷要满足知识点均匀分布在指定范围内的要求,试卷难度、区分度、每种题型的数量等也要符合组卷参数的要求.所以,组卷的过程实际上是求多目标最优解的过程.在网络环境下,组卷策略的好坏在很大程度上影响着组卷效率.理论上,能找到全局最优解的算法往往以时间的延长为代价,要使考试系统具有良好的性能和应用价值, 除了合理的试题库结构外,还必须设计合理的组卷策略.
1 常用的组卷策略
目前,中国国内的考试系统采用的组卷算法多为随机函数法和回溯法.
1.1 随机函数法
该算法的核心思想是利用计算机提供的随机函数或人为设计的随机函数,根据组卷参数的要求,从题库中抽取符合控制指标的试题放入试卷中.该算法结束的条件有两种,组卷成功或无法从题库中抽取满足条件的试题.
该算法的优点是简单、单题抽取效率高、试题分布比较均匀,缺点是多个试卷控制指标之间有时是相互限制的,很难从全局最优化角度抽取试卷,甚至会造成组卷不成功的情况.
该算法在对试卷质量要求不高、组卷参数较少的情况下比较适用,比如学生的自测环节.这是因为学生自测题的选取没有教师的参与,而学生不可能对组卷参数有很深的理解.另外,自测环节对考试公平性的要求较低,不需要很多的参数控制,只要求学生输入要自测的知识点或章节便可以组卷.
实现步骤:学生选择课程和知识点或章节范围,并输入题型和题目个数(m);将题库中所有属于指定课程在指定的知识点或章节范围内的试题号放入一个数组中;用随机函数随机产生m个互不相同的随机数作为数组的下标,然后决定抽取的试题号;在网页上显示试题;完成后在网页上显示答案.
1.2 回溯法
该算法的核心思想是采用深度搜索或广度搜索的方法对题库进行遍历,当找到符合要求的解时,算法终止。回溯法可以系统地搜索一个问题的所有解或任一解,它适用于组卷指标比较简单,出题量较小的组卷.
该算法的优点是比随机法进了一步,组卷成功率较高,缺点是程序结构比较复杂,选取的试题缺乏灵活性,组卷时间较长.
根据以上分析,随机法和回溯法组卷应用于实际的网上考试并不太合适,经过大量的文献阅读和分析,本系统决定使用一种改进的遗传算法.
2 遗传算法
由于遗传算法具有搜索结果全局近优、快速、易实现等特点,成为求多目标最优问题的主流算法.
算法的核心是吸取自然界生物系统的“适者生存,优胜劣汰”的进化思想,先选定一组非劣解的组合作为解的初始群体,然后对初始群体中的个体进行“选择”、“杂交”和“变异”,得到新的个体,从而形成一个临时的新群体,将临时新群体中差的个体淘汰,得到较优良的新群体.不断重复该过程,直到找到一个比较满意的解.
本系统中所使用的遗传算法的基本执行过程如图1所示.
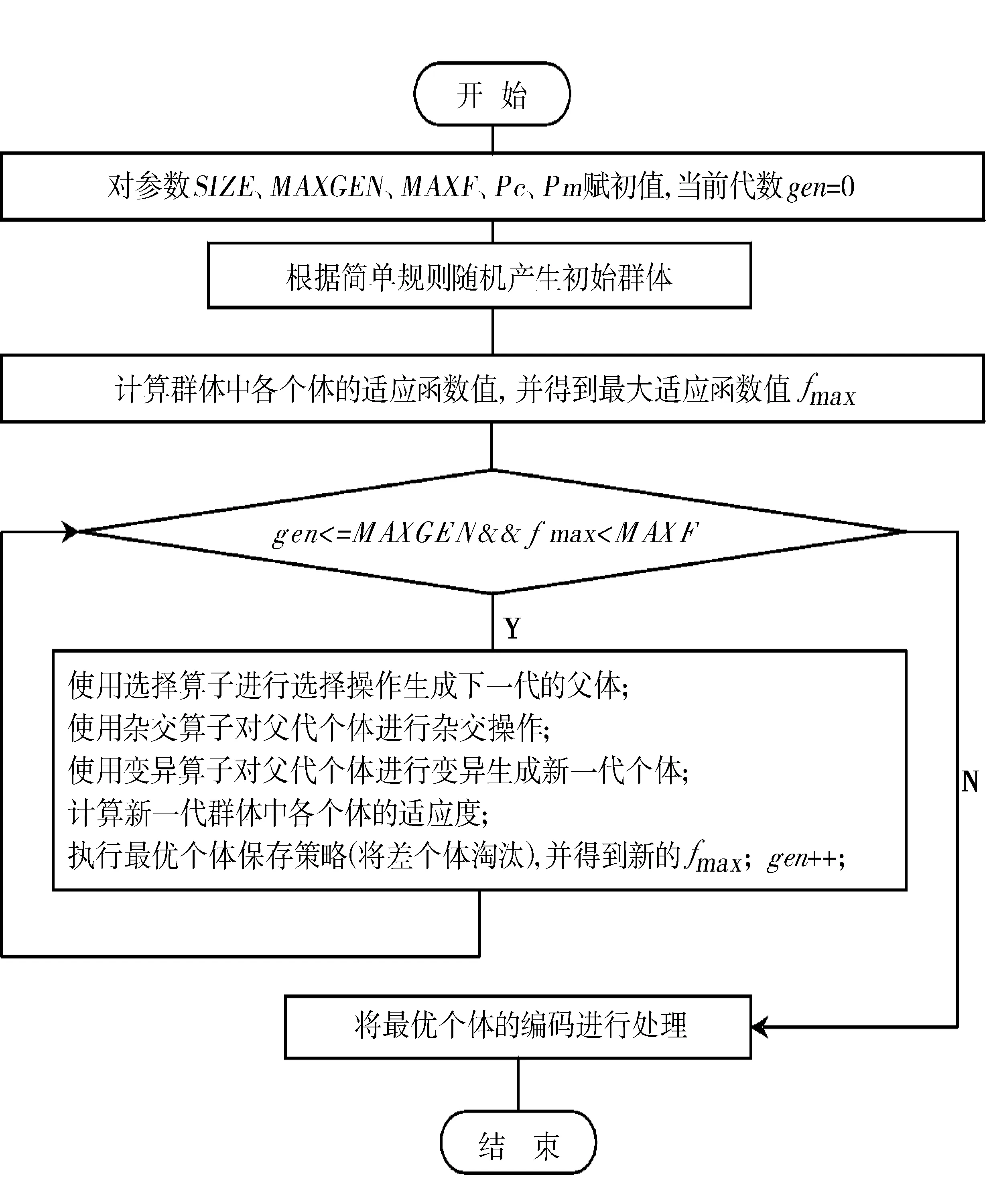
图1 遗传算法流程图Fig.1 Genetic algorithm flowchart
其中,MAXF表示满意的个体的适应函数值;MAXGEN表示最大代数; SIZE表示群体规模;Pc表示杂交概率;Pm表示变异概率.
3 遗传算法在组卷过程中的具体实现
传统型遗传算法存在很多缺点.例如,在初始化群体时适应值较低;算法经过若干代演化运算后,能达到一定的收敛点,但收敛速度较慢,一般需经过200代到300代; 在收敛过程中易陷于局部最优.因此,最后求得的结果适应值较低,有时很难满足组卷的要求[1].国内外学者对遗传算法做了大量的研究和探索,提出了许多有益的改进措施.例如,对适应度进行变换[2],改进新的遗传算子[3]等.本系统采用改进的遗传算法,具体方案如下.
3.1 编码方案
遗传算法不是直接在问题的解空间上求解问题,而是利用解的某种编码进行求解,所以首先要设计编码方案.编码方案有很多种,目前较常用的是二进制编码方案和真值编码方案.二进制编码方案的优点是简单明了,但编码太长,且编码本身不便于反映问题的结构特征.本系统中采用真值编码方案,将一份试卷映射为一个染色体,由组成试卷的各个题目的题号作为染色体的基因值,且将同一题型的基因放在一起.例如,一个试卷中包含5个选择题、5个填空题和2个编程题,各种题型的题目在对应题库中的题号分别为12341235078,315215612365,1051(注意:要求各基因的知识点编号不相同),则染色体编码为:
123412350783152156123651051.
这种编码方式的优点是编码本身已经满足了知识点不重复、题型、题量和总分约束;每种题型逻辑上单独编码,编码短,便于提高遗传算法的局部搜索能力,杂交、变异操作容易实现.
3.2 产生初始化群体
假设每种题型中每个小题的分值相同,教师在设置组卷参数时可以通过控制题型和题量保证总分约束条件的满足,该约束条件在此不做考虑,所以初始种群中的个体只需满足各题型的题目数约束条件和知识点不重复约束条件即可.
对于第一个约束条件,我们采取下面方法保证其成立:设X1、X2、……Xn分别为每种题型在试卷中应有的题目数,Y1、Y2、……、Yn分别为每种题型的题目总数,分别产生X1个不重复的1-Y1区间的随机整数、X2个不重复的1-Y2区间的随机整数、……、Xn个不重复的1-Yn区间的随机整数作为染色体的基因值即可;对于后者,在产生随机题号的过程中判断该题的知识点是否在试卷中出现过,若出现过则作废该随机数,继续进行即可.
3.3 适应函数
适应函数的值是对一个个体好坏评价的唯一指标,适应函数值高的个体被认为是优秀的个体,适应函数的确定依据是组卷目标.
一份好的试卷应满足以下要求:
(1)各题分值之和等于或接近于总分(可以进行局部调整);
(2)题型分布满足指定要求;
(3)知识点分布满足指定的要求;
(4)难度符合指定要求;
(5)区分度符合指定要求.
在此,假设每种题型单题分值相同,则采用前面所述的编码方法可以保障分值和题型分布的要求,只需考虑后3个指标即可.
3.3.1 知识点分布合理程度的衡量
设m为试卷的总题目数,Bi(i=1,2,……,m)表示基因串上第i个题的知识点是否在所要求的知识点范围,如果不在要求范围,取值为1,否则取值为0.在各题目知识点不重复的前提下设计公式1:
(1)
可以推出,f1的值在[0,1]区间上,其值越小,生成的试卷越接近于组卷参数中对知识点分布的要求.
3.3.2 难度系数的衡量
设Xi(i=1,2,……,m)表示考生在第i个题的平均得分,Ai表示第i个题的满分,Di表示第i个题的难度系数,则Di=1-X/Ai,试卷总体难度系数ND的计算方法如公式2所示:
(2)
设组卷参数中的难度系数为ND1,则设计公式3.
f2=|ND-ND1|
(3)
可以推出,f2的值在[0,1]区间上,其值越小,生成的试卷的难度系数越接近于组卷参数中难度系数的要求值.
3.3.3 区分度的衡量
区分度是指使水平高的学生得高分、水平低的学生得低分的倾向力.设P表示区分度,Rh为高分组(前27%的被测试者)在该题上的平均分,Rl为低分组(后27%的被测试者)在该题上的平均分,Ai表示该题的满分,则P=(Rh-Rl)/Ai.
设Pi(i=1,2,……,m)是基因串上第i个题的区分度,Ai表示第i个题的满分,则试卷的总体区分度NP的计算方法如下:
(4)
设组卷参数中的区分度为NP1,则设计公式5:
f3=|NP-NP1|
(5)
可以推出,f3的值在[0,1]区间上,其值越小,生成的试卷的总体区分度越接近于组卷参数中区分度的要求值.
最后,得到适应函数f4=f1+f2+f3(f2和f3的计算公式中取绝对值是为了避免两种误差相互抵消[4]),f4在[0,3]区间,且其值越小越好.为了提高相近个体间的竞争,也为了适应“适应函数值越大个体越优秀”的习惯说法,本系统中最终采用的适应函数如下:
f=-100(f1+f2+f3)+300
(6)
3.4 选择算子、杂交(交叉)算子和变异算子
选择算子使得适应函数值高的个体有较高的存活率,用来对群体中的个体进行优胜劣汰操作,使优秀的个体遗传到下一代的概率较大,差的个体遗传到下一代的概率较小.选择算子有很多种,本系统采用“赌盘选择法”和“最优保存法”[5]相结合的策略.已经有学者证明,传统遗传算法只能找到局部最优解,而不能得到全局最优解[6],最优保存法使简单遗传算法具有全局收敛性[7].所以,最优保存策略已作为一种保证遗传算法收敛的通用手段来使用.
最优保存策略的基本思路为设当代种群为oldpop,计算oldpop中各个体的适应值,并找出最优个体;对oldpop进行选择、交叉和变异操作得到新的种群newpop;计算newpop中各个体的适应值,并找出最劣个体;用oldpop中的最优个体替换newpop中的最劣个体,最后得到一个和原始种群规模相同规模的新种群.
各个体被选中进行杂交和变异的概率与其适应度函数值成正比,被选中后,进行杂交和变异操作得到新个体.
杂交算子常用的有“单点交叉”、“双点交叉”和“均匀交叉”[4].本系统中选用“均匀交叉”,每对配对的个体上的所有基因对都按照相同的杂交概率进行杂交(进行交叉的基因对的数量由交叉概率Pc决定),形成两个新个体.
变异算子[4]:将染色体上的某个(多个)基因值用随机产生的另外一个等值基因值替换,从而形成一个新的个体.变异的多少取决于变异概率Pm的大小,一般取Pm*题量.
3.5 算法结束的条件
一般有两种结束条件,进化到最大代数(MAXGEN)或得到较满意的个体(最优个体的适应函数值达到要求值MAXF),所以需确定MAXGEN的值,该值实际上需要通过实验获得,本系统暂时取类似系统所提供的参考值50[8],在以后的运行过程中再根据统计数据进行调整.
3.6 控制参数的取值
种群规模(SIZE)、杂交概率(Pc)和变异概率(Pm),这些参数都是算法的重要数据依据.
(1)种群规模:此参数较大时组卷收敛速度较慢,但易搜索到全局最优解,反之,则收敛速度快,但不易搜索到全局最优解,一般取种群规模30~60[8].
(2)杂交概率(Pc)和变异概率(Pm):这两个参数如果取值太大,可能使算法变成纯粹的随机搜索算法[9],Pc若过小,组卷收敛速度会变慢,参考取值为0.25~0.85;Pm若过小,则不容易产生新个体,参考取值为0.01~0.25[10].
在本系统中,采用自适应思想[8],在算法进行过程中,Pc和Pm可以根据实际情况自行调整,使其随适应函数值的增大而变小,随其变小而增大.设f为两个交叉个体的适应函数值的较大值,favg为群体适应函数值的平均值,fmax为群体中适应函数值的最大值,f′为变异个体的适应函数值,Pc和Pm的计算方法如公式7和8所示.
(7)
(8)
4 乱序引擎的使用
本系统采用的是一个考场在同一时间使用一份试卷、每个考生的考题顺序都不一样的策略,那么就存在怎样将题号打乱的问题.
设待打乱的题目数为M,该问题的实质是产生M个1~M之间的不重复的随机数.一般的算法是每产生一个随机数就和前面产生过的随机数进行比较,如果有相同的随机数已经在序列中存在,则该随机数作废.可以证明,该算法的算法复杂度为O(M2),因为该算法要经常被用到(比如一场考试有300个人参加,则需要调用300次),所以最好能降低其时间复杂度.本考试系统采用乱序引擎[11]算法完成此工作.该算法的步骤如下.
将原始题目序号放入A[1]~A[m];
i=1;
while (i<=m)
{ 产生一个[1,m]区间的随机数x;
将A[x]和A[i]交换;
i++; }
由于题目序号不重复,每次又是两两交换,所以不可能有重复的题号.该算法的时间复杂度为O(M),且空间效率也没有降低.
5 结 语
对遗传算法的各个环节进行了具体分析和描述,本算法思想已经使用Java代码实现.实践证明,使用改进的遗传算法实现组卷过程是行之有效的,具有较好的推广价值.
参考文献:
[1] 李美满, 夏汉铸, 易德成. 基于COM 技术的通用考试系统的设计与实现[J].计算机工程与应用, 2007, 43(1): 245-248.
[2] KREINOVICH V, QUINTANA C, FUENTES O.Genetic algorithms-what fitness scaling is optimal[J].Cybernetics and System,1993,24(1):9-26.
[3] 郑金华,叶正华.基于空间交配的遗传算法[J].模式识别与人工智能,2003,16(4):482-485.
[4] BESSAOU M,SLARRY P.A genetic algorithm with real-value coding to optimize multimodal continuous functions[J].Structure Multitask Optimization,2001,23(1):63-74.
[5] GREFENSTETTE J J.Optimization of control parameters for genetic algorithms[J]. IEEE Transactions on Systems, Man and Cybernetics, 1986, 16(1): 122-168.
[6] RUDOLPH G.Convergence properties of canonical genetic algorithms[J].IEEE Transactions on Neural Networks,1994, 5(1):96-101.
[7] 恽为民,席裕庚.遗传算法的全局收敛性和计算效率分析[J].控制理论与应用,1996,13(4):455-460.
[8] 周文举. 一种基于知识点的遗传算法组卷的改进应用[J].山东师范大学学报:自然科学版, 2006, 21(3):39-42.
[9] 杨路明, 陈大鑫. 改进遗传算法在试题自动组卷中的应用研究[J].计算机与数字工程,2004,32(5):76-79.
[10] 刘韶丽. 基于智能组卷策略的网上考试系统的设计与实现[D].南京:东南大学,2006.
[11] 陆宏谦.基于J2EE构架的网上考试系统的分析与设计[D].济南:山东大学, 2005.
