相关阴影Rician衰落信道上MPSK的性能

0 引言

衰落信道上空时分组码(Space-Time Block Code,STBC)的性能研究是当前无线通信的研究热点。文献1推导了平坦瑞利衰落信道上STBC编码的M进制相移键控(M-ary Phase Shift Keying,MPSK)平均符号错误概率(Symbol Error Probability,SEP)的闭合表达式。文献2推导了平坦Nakagami衰落信道上STBC编码的MPSK平均SEP性能的精确闭合表达式。文献3推导了相关Nakagam i衰落信道上STBC编码的MPSK平均SEP性能的精确闭合表达式。相关阴影Rician衰落信道模型是陆地移动卫星系统的典型信道模型,文献4推导了相关阴影Rician衰落信道上STBC编码的MPSK平均误比特率(Bit Error Rate,BER)性能的精确闭合表达式。文献4局限于研究MPSK的平均BER性能,对于MPSK精确的平均SEP性能没有给出相应的研究成果。为此,本文研究相关阴影Rician衰落信道上STBC编码的MPSK的平均SEP性能。

1 系统模型

考虑发射天线数为nT、接收天线数为nR的相关阴影Rician衰落信道上采用STBC的MPSK调制系统。假设信道为准静态平坦衰落信道,即信道参数至少在一个完整的帧传输周期(T个时隙)内保持恒定;接收端具有理想的信道状态信息,发射端对于信道状态信息则是未知的;在T个时隙内发送了K个符号,则STBC的编码速率为Rs=K/T,其中最具代表性的2根和3根发射天线的STBC编码,分别是全速率编码G2、3/4速率编码H3和速率编码G3[5]。每个STBC可以用一个nT×T矩阵X来表示,系统的输入输出关系可表示为Y=HX+N,其中nR×T矩阵Y为接收信号矩阵,nR×T矩阵N为噪声矩阵,其元素都为独立同分布的复高斯随机变量,服从CN(0,N0)分布。

考虑文献4中相关视距(Line-Of-Sight,LOS)分量、独立散射分量的情况,即nR×nT信道矩阵为H=HL+HS,其中HS=表示散射分量,RT和RR分别为nT×nT和nR×nR单位矩阵,(◦)1/2表示矩阵的厄米特平方根,HW中的元素均为独立同分布的复高斯随机变量,均值为零,方差为每维0.5;HL=[Zj,k]j=1,…,nR;k=1,…,nT表示LOS分量,其中元素Zj,k为相关Nakagam i-m分布随机变量,其边缘概率密度函数为 pZj,k(Zj,k)=(2mm/Γ(m)Ωmexp(-/Ω),Zj,k≥0,m≥0.5。令Zn,n=1,2,…,nRnT表示矢量化算符vec(HL)中第n个元素,φu,v=E()/Ω定义了元素Zu和Zv之间的相关性,E(◦)为求数学期望,则LOS分量的相关矩阵可表示为△=[φu,v]u=1,…,nRnT;v=1,…,nRnT。假设λ1,λ2,…,λN为△的N 个递减的非零特征根,其重根数分别为u1,u2,…,uN,则非零特征根的总数为R=u1+u2+…+uN。基于等效的单输入单输出信道模型,接收端输出每个符号的瞬时信噪比(Signal-to-Noise Ratio,SNR)为γ=cρ‖H ‖2,‖H ‖2表示矩阵H的Frobenius范数的平方,ρ为每根接收天线的平均SNR,c=1/(RsnT),则瞬时SNRγ的矩生成函数可表示为[4]:

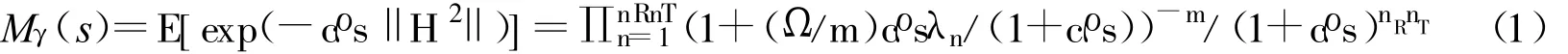
当信道衰落参数m为正整数时,将式1通过部分分式法展开,可推得:

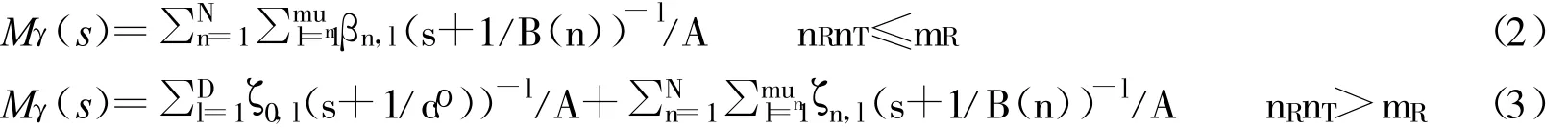
2 MPSK的平均SEP性能

加性高斯白噪声信道上相干MPSK的条件SEP为[1]:

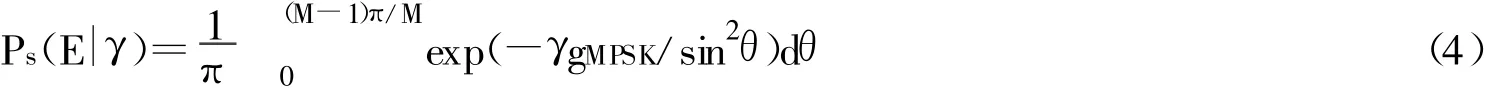
式中,gMPSK=sin2(π/M)。利用接收端输出瞬时SNRγ的概率密度函数对式4求统计平均,即可得到相关阴影Rician衰落信道上STBC编码的MPSK的平均SEP为:

式中,Mγ(s)可以由式1给出,将式1代入式5,可得:

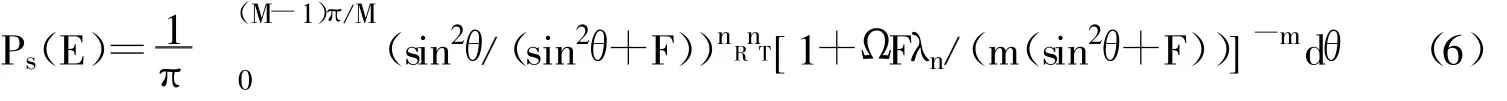
式中,F=cρgMPSK,此时所得MPSK平均SEP表达式不是闭合的表达式,需要进行数值积分运算。当信道衰落系数m为正整数时,式5中的Mγ(s)可以由式2或3给出。

(1)nRnT≤mR时,将式2代入式5,可得:

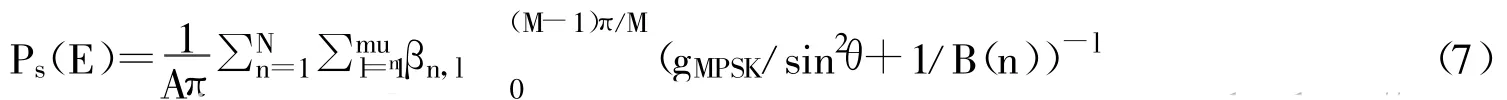
对式7的积分项中提取系数B(n)l,并动用文献6中式6,可推得:

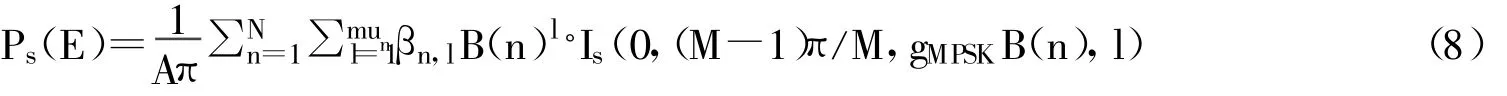
式中,Is(θL,θU,b1,b2)的定义由文献6的式A.3给出。

(2)nRnT＞mR时,将式3代入式5,可得:

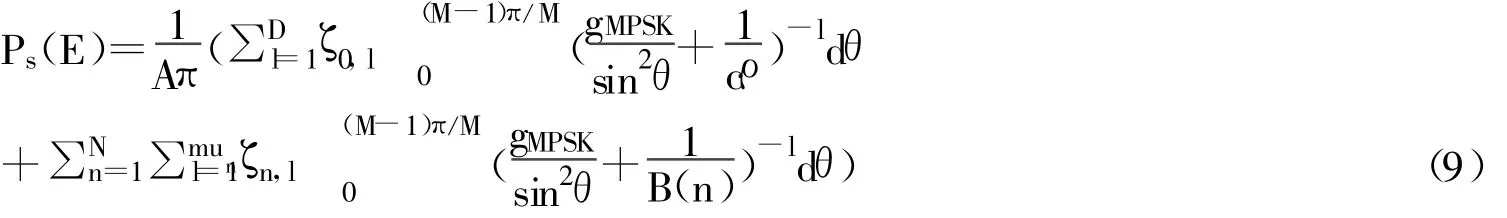
对式9的两个积分项中分别提取系数(cρ)l和B(n)l,并动用文献6中式A.3,可推得:

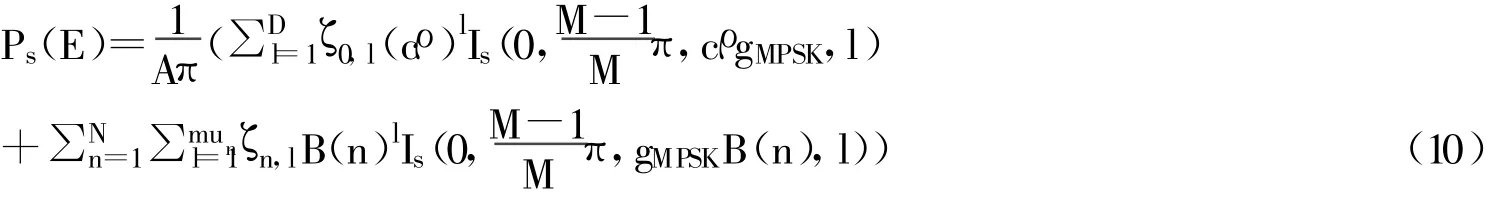
由此,可得到相关阴影Rician衰落信道上STBC编码的MPSK平均SEP性能的精确闭合表达式。

3 数值计算结果

本文有选择性地给出一些数值计算结果来说明信道衰落参数m、Ω和空间相关性对MPSK平均SEP性能的影响。首先考虑nT=2的情况,此时LOS分量的相关矩阵为△=[1,Ψ;Ψ,1]。m=3、Ω=0.1和Ψ=0.9条件下采用G2编码时BPSK、QPSK、8PSK和16PSK的平均SEP性能如图1所示。由图1可知,MPSK的平均SEP性能随着星座大小M的增大而恶化。SNR=15dB、Ψ∈{0,0.5,0.9}以及Ω∈{0.1,0.11,0.12}时在不同m条件下采用G2编码时8PSK的平均SEP性能如图2所示。nT=3、m=3、Ω=0.1、SNR=10dB以及(Ψ2,Ψ3)∈{(0,0),(0.2,0.2),(0.4,0.4)}时在不同 Ψ1条件下采用H3编码时QPSK的平均SEP性能如图3所示,此时阴影Rician信道中LOS分量的相关矩阵为△=[1,Ψ1,Ψ2;Ψ1,1,Ψ3;Ψ2,Ψ3,1]。由图3可知,QPSK的平均SEP性能随着 Ψ1的增大得到恶化。SNR=15dB、Ψ1=0.2、Ψ2=0.2以及 Ψ3∈{0,0.5,0.9}、Ω∈{0.1,0.11,0.12}时在不同m条件下采用G3编码时8PSK的平均SEP性能由图4所示。由图2和图4可知,8PSK的平均SEP性能随着m或/和Ω的增大得到改善,而且分别随着Ψ和 Ψ3的增大得到恶化。

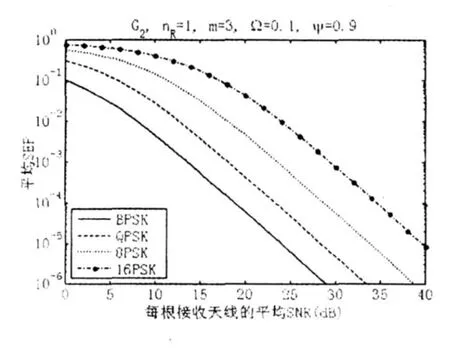
图1 相关阴影Rician信道上MPSK的平均SEP性能

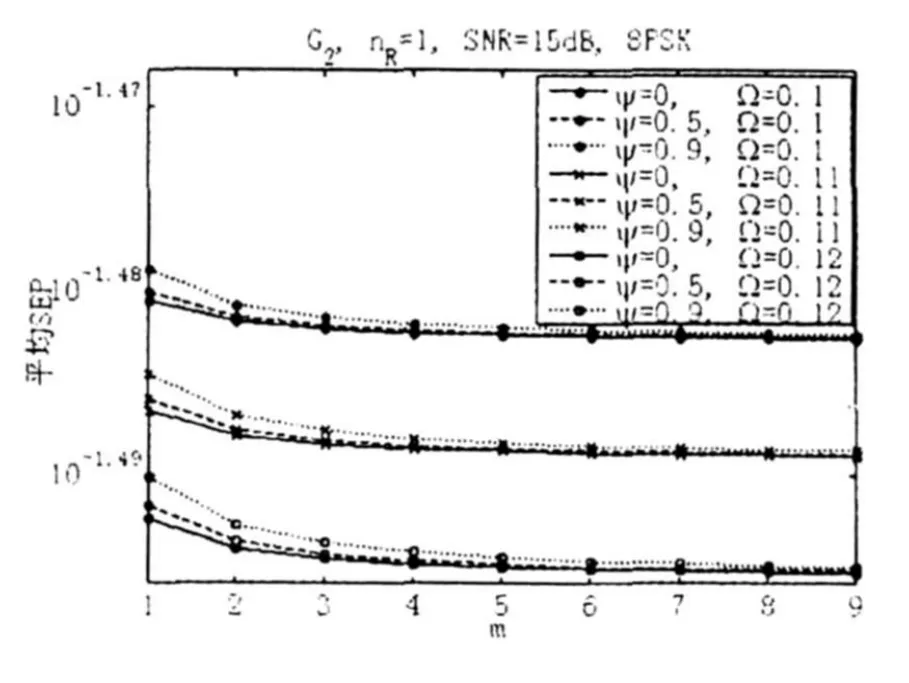
图2 m和 Ψ对8PSK平均SEP性能的影响

4 结论

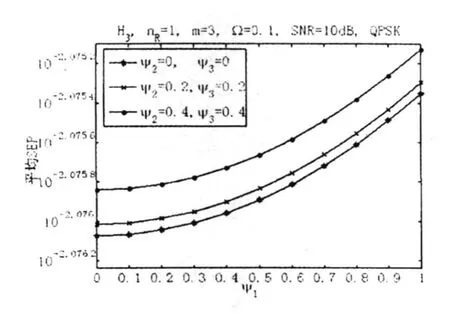
图3 对QPSK平均SEP性能的影响

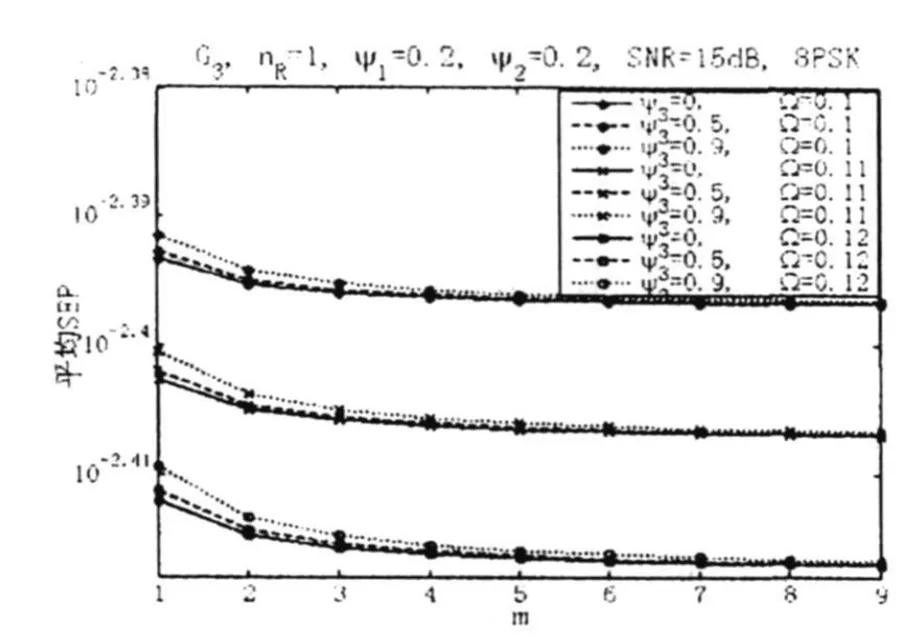
图4 m和 Ψ3对8PSK平均SEP性能的影响

本文使用矩生成函数方法,推导了相关LOS分量、独立散射分量条件下的阴影Rician衰落信道上采用STBC编码的MPSK平均SEP性能的精确闭合表达式。利用该闭合表达式计算MPSK的平均SEP性能避免了复杂的积分运算,有效地降低了计算复杂性。数值计算结果表明,信道衰落系数或/和的增大改善了MPSK的平均SEP性能;天线间的相关性恶化了MPSK的平均SEP性能。

[1] Shin H,Lee JH.Exact symbol error probability of orthogonal space-time block codes[C].Taipei:Global Telecommunication Conference,2002:1 197-1 201.

[2] Xu F,Yue DW.Exact error probability of orthogonal space-time block codes over fading channels[C].Chengdu:6th International Conference on ITS Tele communications Proceedings,2006:469-472.

[3] Maaref A,Aissa S.Performance analysis of orthogonal space-time block codes in spatially correlated MIMO Nakagami fading channels[J].IEEE Transactions on Wireless Communications,2006,5(4):807-817.

[4] Kim IM.Exact BER analysis ofOSTBC in spatially correlated MIMO channels[J].IEEE Transactions on Communications,2006,54(8):1 365-1 373.

[5] Tarokh V,Jafarkhani H,Chalderbank A R.Space-time block coding for wireless communications:performance results[J].IEEE Trans Sel Areas Commun,1999,17(3):451-460.

[6] Annamalai A,Tellambura C.Error rates for Nakagami-fading multichannel reception of binary and M-ary signals[J].IEEE Transactions on Communications,2001,49(1):58-68.